Как решить магический квадрат: учимся решать одну из древнейших задач

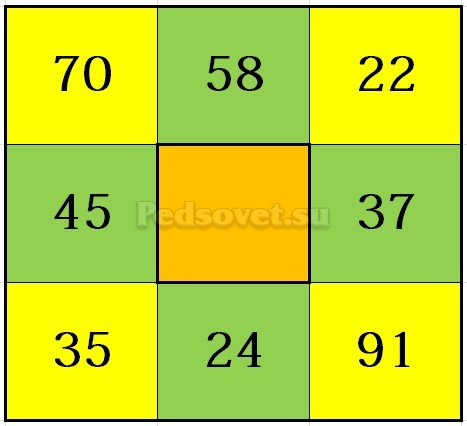
Магический квадрат представляет собой квадратную таблицу с числами, построенную так, что сумма чисел в каждой строке, каждом столбце и в каждой диагонали равна одному и тому же числу (магическая сумма). Магические квадраты бывают разных порядков — порядок квадрата определяет число столбцов/строк. Как рассчитать и решать магические квадраты?

Археологи нашли свидетельства того, что волшебные таблицы были известны еще древним грекам и китайцам. «Магическими» эти фигуры назвали арабы, которые наделяли их сверхъестественными защитными свойствами.

В середине XVI в. европейские математики занялись исследованиями загадочных таблиц, положив начало их новой жизни. Они искали общий метод построения магических квадратов и пытались описать все возможные их варианты.

На уроках математики в школе

Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.

Один из способов решения магического квадрата

Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:

1. Вписываем в первую строку или столбец 3 любых числа.

pedsovet.su

Правила магических квадратов

Меотдические указания
для практических занятий
по курсу:
Разработка ПО САПР
на тему:
Построение магического квадрата.

Цель занятия:Целью занятия является практическое изучение способов объектно-ориентированной обработки 2-мерных массивов в системе программирования С++ для составления магических квадратов, которые являются популярным примером кросс-сумм теории чисел.

Формулировка задания:Требуется разработать программу magic для составления магических квадратов четного и нечетного порядка в произвольном диапазоне натуральных чисел. Исходными данными программы magic считаются порядок и арифметическая прогрессия элементов магического квадрата. Исходные данные передаются программе через аргументы командной строки ее вызова. В результате работы программы magic должна быть построена матрица элементов и вычислена константа магического квадрата. Результат работы программы должен отображаться через поток стандартного вывода.

Понятие магического квадрата

Под магическим квадратом порядка N понимается квадратная матрица размером NxN из N в квадрате последовательных элементов произвольной арифметической прогрессии натуральных чисел, которые размещены так, что суммы элементов любого столбца, строки или главной диагонали одинаковы. Результат вычисления любой из перечисленных сумм принято называть константой логического квадрата. Порядок магического квадрата определяется числом элементов любого столбца или строки. Например, магический квадрат 3-го порядка из 9-ти 1-х натуральных чисел (известный в Китае как талисман ло-шу) представляется следующей матрицей 3×3:

Константа квадрата ло-шу равна 15. Это единственный квадрат 3-го порядка, который можно построить из натуральных чисел от 1 до 9, если не использовать преобразований поворота и отражения. Классический образец магического квадрата 4-го порядка, известный еще в Древней Индии, представляется следующей матрицей 4×4:

Константа «индийского» квадрата равна 34. В несколько измененном виде (достигаемом перестановкой строк и столбцов):

он известен художникам по филосовской гравюре А. Дюрера «Меланхолия». Астрологи средних веков приписывали числовым сочетаниям магических квадратов таинственные и волшебные свойства. Современных математиков и программистов интересуют формальные методы составления магических квадратов.

Составление магических квадратов нечетного порядка

Наибольший практический интерес представляют универсальные методы, которые не зависят от порядка магического квадрата. Такие методов известны для магических квадратов нечетного порядка. Наиболее наглядный из них удобно рассмотреть на примере составления магического квадрата 5-го порядка из натуральных чисел от 1 до 25. Алгоритм этого метода включает следующие шаги.

1. Сначала исходный пустой квадрат достраивается до симметричной ступенчатой ромбовидной фигуры как показано на следующем рисунке, где ячейки для элементов квадрата обозначены символом #, а достроенные ячейки — символом $.

3. Каждое число, расположенное в фигуре шага 2 вне исходного квадрата, переносится по вертикали или горизонтали внутрь исходного квадрата на число позиций, равное порядку квадрата. В рассматриваемом примере перенос осуществляется на 5 позиций. Таблица переносов имеет следующий вид:

Освобождающиеся ячейки, достроенные к исходному квадрату заполняются символом $.

4. После преобразования переноса на шаге 3 освободившиеся ячейки (заполненные символом $) должны быть исключены. Оставшиеся (внутренние) ячейки (заполненные натуральными числами) образуют магический квадрат, представленный следующей матрицей 5×5:

константа которого равна 65, что может быть проверено вычислением суммы элементов для столбцов, строк и главных диагоналей.

Рассмотренный метод составления нечетных магических квадратов не является единственным. Не менее известным и не более сложным является следующий алгоритм, предложенный С. Лубером. Правила алгоритма Лубера удобно иллюстрировать на примере магического квадрата порядка 7 из натуральных чисел от 1 до 49, матрица 7×7 которого показана на следующем рисунке:

В основе алгоритма лежит заполнение ячеек квадрата в направлении вверх и влево по диагонали последовательными числами выбранной арифметической прогрессии. Заполнение начинается со среднего элемента верхней строки (01). Если следующая левая диагональная ячейка уже занята числом (ячейка 01 уже занята в момент заполнения ячейки 07), нужно перейти к нижнему соседу (08) текущей заполненной ячейки (07) и продолжить движение по диагонали. Чтобы избежать возможности выхода за границы квадрата при диагональном его надо мысленно превратить в тор, соединив верхнюю горизонталь с нижней, а затем соединить основания полученного цилиндра. После свертки строки, столбцы и диагонали квадрата превращаются в замкнутые кривые на поверхности тора и выход за границы квадрата становится невозможным. Превращение квадрата в тор в данном случае обеспечивает возможность диагонального перехода, например, из ячейки 01 в ячейку 02 или из ячейки 45 в ячейку 46.

Составление магических квадратов в четном порядке

Универсальные методы составления магических квадратов произвольного четного порядка пока неизвестны. Однако, разработаны индивидуальные подходы для различных частных случаев. Ниже рассмотрен метод составления магических квадратов, порядок которых является экспонентой 2. Этот метод удобно рассмотреть на примере магического квадрата 8-го порядка из натуральных чисел от 1 до 64. Метод включает следующую последовательность шагов.

1. Исходный квадрат делится на соответствующее число квадратов порядка 4. В данном случае таких квадратов будет 4. В каждом подквадрате отмечаются диагональные элементы (например, символом #). Остальные элементы построчно заполняются порядковыми целыми числами в направлении слева-направо и сверху-вниз. Числа, приходящиеся на выделенные диагональные элементы должны быть пропущены. Результат заполнения недиагональных элементов квадрата 8-го порядка показан на следующем рисунке:

Константа этого магического квадрата равна 260, что подтверждается вычислением контрольных сумм элементов по строкам, столбцам и главным диагоналям.

Программирование магических квадратов

Для программирования магических квадратов удобно использовать парадигму инкапсуляции объектно- ориентированного программирования, сосредоточив «магические» структуры данных и методы их обработки в отдельном классе Magic. В класс Magic рекомендуется включить следующие приватные (privat) компоненты — данные:

unsigned degree — порядок квадрата;

unsigned basic, differ — начальный элемент и разность арифметической прогрессии натуральных чисел, заполняющих магический квадрат;

unsigned **tab — указатель на двумерный массив беззнаковых целых чисел, который должен содержать матрицу магического квадрата.

Для обработки приватных данных в классе Magic целесообразно предусмотреть следующие общедоступные (public) компонентные методы:

void magodd( ) — формирует магический квадрат нечетного порядка;

void mageven2( ) — составляет магический квадрат четного порядка, у которого порядок является экспонентой 2;

int chksum( ) — вычисляет контрольные суммы элементов столбцов, строк и главных диагоналей квадрата, возвращая величину константы квадрата или 0, если квадрат не является магическим;

void print( ) — отображает матрицу и константу магического квадрата в потоке стандартного вывода;

void magbuild( ) — вызывает метод составления, соответствующийпорядку магического квадрата.

Для инициализации компонент-данных в классе Magic следует предусмотреть конструктор. Конструктор класса Magic должен иметь возможность принимать 3 аргумента, определяющих порядок, начальный элемент и разность арифметической прогрессии элементов магического квадрата. При декларации конструктора рекомендуется указать значения аргументов по умолчанию:

Magic(unsigned=3, unsigned=1, unsigned=1);

Это позволит для создания объектов класса Magic использовать вызов конструктора в сокращенном формате; с одним , двумя или без аргументов. Например, следующий вызов конструктора:

является корректным для составления магического квадрата ло-шу, где приватные компоненты-данные degree, basic, differ по умолчанию инициализируются величинами 3, 1, 1, соответственно. Кроме инициализации целочисленных компонент-данных конструктора класса Magic желательно поручить динамическое распределение памяти, необходимое для хранения 2-мерного массива элементов магического квадрата tab. Для динамического распределения памяти под 2-мерный массив рекомендуется использовать следующую 2-х этапную схему:

1. распределить память под 1-мерный массив указателей на беззнаковые целые размером degree по адресу tab используя оператор new:

tab=new unsigned *(degree);

2. под каждый указатель полученного массива указателей распределить одномерный массив беззнаковых целых из degree элементов, используя оператор new в цикле:

Рассмотренный способ формирования 2-мерного массива позволит обращаться к любому j-му элементу i-й строки в компонентных методах класса Magic традиционным образом tab[i][j]. Вызов компонентных методов составления магического квадрата может быть реализован в теле конструктора класса Magic, а обращение к компонентному методу отображения результатов целесообразно организовать в основной функции программы magic.

После завершения требуемой обработки и отображения результатов объекты класса Magic должны быть уничтожены с помощью деструктора

Magic( ). Деструктор класса Magic должен освободить память, динамически распределенную конструктором по адресу tab для хранения 2-мерного массива элементов магического квадрата. Рекомендуется освобождать память по схеме обратной ее распределеню, используя оператор delete:

1. освободить память, распределенную под degree одномерных массивов беззнаковых целых (из degree элементов каждый) по адресам от tab[0] до tab[degree-1]:

2. освободить память, распределенную под 1-мерный массив указателей на беззнаковые целые, состоящий из degree указателей по адресу tab:

delete [degree]tab; Обычно деструктор вызывается неявно при завершении работы с объектом класса, например, после выхода из блока, где объект был определен. При необходимости явного вызова деструктора в обращении к нему должно быть специфицировано имя класса, которому он принадлежит:

В соответствии с принципами структурного программирования следует разместить декларацию класса Magic в отдельном заголовочном h-файле. Исходный код компонентных методов класса Magic и основной функции main( ) программы magic, которая оперирует ими, рекомендуется разместить в 2-х отдельных файлах. Для успеха трансляции в каждый из них нужно включить заголовочный файл класса Magic, используя директиву include.

1. Определить зависимость величины центрального элемента магического квадрата нечетного порядка и константы квадрата.

2. Разработать специальный компонентный метод в классе Magic, который формирует магический квадрат ло-шу, используя следующий алгоритм. Заполнить изначально пустой квадрат размером 5×5 целыми числами от 1 до 9, располагая их последовательно в строках и столбцах с нечетными номерами. Затем следует поменять местами цифры на противоположных концах главных диагоналей и придвинуть их на 1 позицию в направлении к центру квадрата. После этих преобразований 3 группы элементов матрицы 5×5 с одинаковыми суммарными индексами строк и столбцов, равными 4, 6 и 8, соответственно, образуют строки искомого магического квадрата ло-шу.

3. Средние числа в нижней строке магического квадрата А. Дюрера отображают год — 1514, когда им была создана гравюра «Меланхолия», содержащая этот магический квадрат 4-го порядка из 1-х 16-ти натуральных чисел. Применяя перестановку строк и столбцов квадрата А. Дюрера, требуется найти другие магические квадраты, где тот же год фигурирует таким же образом. Для решения этой проблемы рекомендуется расширить класс Magic компонентными методами перестановки строк и столбцов квадратов.

4. Разработать класс Multimag для формирования магических квадратов, у которых произведения элементов в каждой строке, столбце и главной диагонали равны. Для заполнения ячеек квадрата следует использовать члены геометрических прогрессий, у которых начальный элемент и знаменатель прогрессии равны (например, последовательности степеней 2, 3 и других натуральных чисел).

5. Расширить класс Magic компонентным методом mageven6( ) для формирования магического квадрата 6-го порядка на основе следующего алгоритма. Формируемый магический квадрат разбивается на 4 подквадрата 3-го порядка, которые заполняются соответствующим алгоритмом составления магического квадрата нечетного порядка. Подквадраты заполняются в такой последовательности: левый верхний, правый нижний, правый верхний, левый нижний. После заполнения подквадратов необходимо поменять местами элементы левых полудиагоналей у 2-х левых квадратов 3-го порядка.

6. Модифицировать конструктор класса Magic, введя для инициализации целочисленных компонент-данных список инициализаций вместо их инициализации внутри тела конструктора.

7. Модифицировать класс Magic, дополнив его конструктором копирования-инициализации, спецификация которого имеет вид:

Аргументом этого конструктора является ссылка на объект класса Magic, точной копией которого должен быть создаваемый объект.

1. Б. А. Коргмский

Математическая смекалка, — М., ТТЛ, 1957г.

Математические головоломки и развлечения, — М., Мир, 1971г.

Приглашение в теорию чисел, — М., Наука, 1980г.

Язык программирования TURBO C++, — М., МГУ, 1991г.

cad.narod.ru

Правила построения магических квадратов составление магических квадратов

ХIII научно-практическая конференция школьников

Ученицы 8 «А» класса

Руководитель Анохина М.Н.

История создания моей работы………………………………………………2

Магический квадрат. 3

Исторически значимые магические квадраты. 4-5

КВАДРАТ, НАЙДЕННЫЙ В КХАДЖУРАХО(ИНДИЯ). 6

Магический квадрат Ян Хуэя (Китай). 7

Квадрат Альбрехта Дюрера . 8

Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл. 9

Дьявольский магический квадрат . 10-11

ПРАВИЛА ПОСТРОЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ . 12

СОСТАВЛЕНИЕ МАГИЧЕСКИХ КВАДРАТОВ. 13-15

Создание магического квадрата Альбрехта Дюрера. . 17-18

Судоку. 19-21 Какуро. 22-23

БАНК ЗАДАЧ. 24-25

Выводы. 26 Литература. 27

Раньше я даже не задумывалась, что такое можно придумать. Первый раз магические квадраты встретились мне в первом классе в учебнике, они были самые простые.

Через несколько лет с родителями я поехала на море познакомилась с девочкой, которая увлекалась судоку. Мне тоже захотелось научиться, и она объяснила, как это делать. Это занятие мне очень понравилось, и оно стало моим так называемым хобби.

После того как мне предложили участвовать в научно-практической конференции, я сразу выбрала тему «Магические квадраты». В этой работу я включила исторический материал, разновидности, правила создания игру-загадку.
Магический квадрат.

Магический, или волшебный квадрат-это квадратная таблица, заполненная n числами, таким образом, что сумма чисел в каждой строке, в каждом столбце и на обеих диагоналях оказывается одинаковой. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n .

Магические квадраты существуют для всех порядков, за исключением n=2, хотя случай n=1 тривиален — квадрат состоит из одного числа.

Сумма чисел в каждой строке, столбце и на диагоналях. Называется магической константой , М. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой.

Первые значения магических констант приведены в следующих таблице.

Исторически значимые магические квадраты.

В китайской древней книге «Же-ким» («Книга перестановок») приводится легенда о том, что император Ню, живший 4 тысячи лет назад, увидел на берегу реки священную черепаху. На её панцире был изображен рисунок из белых и черных кружков(рис.1). Если заменить каждую фигуру числом, показывающим сколько в ней кружков, получится таблица.

У этой таблицы есть замечательное свойство. Сложим числа первого столбца: 4+3+8=15.тот же результат получится при сложении чисел второго, а так же третьего столбцов. Он же получается при сложении чисел любой из трех строк. Мало этого, тот же ответ 15 получается, если сложить числа каждой из двух диагоналей: 4+5+6=8+5+2=15.

Наверное, эту легенду китайцы придумали, когда нашли расположение чисел от 1 до 9 со столь замечательным свойством. Рисунок они назвали «ло-шу» и стали считать его магическим символом и употреблять при заклинаниях. Поэтому сейчас любую квадратную таблицу, составленную из чисел и обладающую таким свойством, называют магическим квадратом.

КВАДРАТ, НАЙДЕННЫЙ В КХАДЖУРАХО(ИНДИЯ).

Самый ранний уникальный магический квадрат обнаружен в надписи ХI века в индийском городе Кхаджурахо.

Это первый магический квадрат, относящийся к разновидности так называемых «дьявольских» квадратов.

Магический квадрат Ян Хуэя (Китай)

В XIII веке математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были, потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков.

Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка.

Квадрат Альбрехта Дюрера

Магический квадрат 4х4, изображенный на гравюре А. Дюрера «Меланхолия I», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания картины(1514)

Сумма чисел на любой горизонтали, вертикали и диагонали равна 34 . Эта сумма также встречается во всех угловых квадратах 2х2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+8+9+15 и 3+5+12+14), прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12).Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.

Если в квадратную матрицу n х n заносится нестрого натуральный ряд чисел, то данный магический квадрат — нетрадиционный. Ниже представлены два таких магических квадрата, заполненные в основном простыми числами. Первый (рис.3) имеет порядок n=3 (квадрат Дьюдени); второй (рис.4) (размером 4х4)- квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия.

Дьявольский магический квадрат

Дьявольский магический квадрат — магический квадрат, в которой также с магической константой совпадает сумма чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.

Такие квадраты называют ещё пандиагональными .

Существует 48 дьявольских магических квадратов 4х4 с точностью до поворотов и отражений. Если принять во внимание ещё и их дополнительную симметрию – торические параллельные переносы, то останется только 3 существенно различных квадрата:

Однако было доказано, что (рис.7) простейшими перестановками чисел получаются первые два квадрата (рис.5;6). То есть третий вариант- это базовый дьявольский квадрат, из которого различными преобразованиями можно построить все остальные.

Пандиагональные квадраты существуют для нечётного порядка n>3, для любого порядка двойной чётности n=4k (k=1,2,3…) и не существуют для порядка одинарной чётности n=4k+2 (k=1,2,3…).

Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных пандиагональных квадратов нечётного порядка не существует. Среди пандиагональных квадратов чётности выше 4 имеются совершенные.

Пандиагональных квадратов пятого порядка 3600. С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.

ПРАВИЛА ПОСТРОЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ

Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы.

Найти все магические квадраты порядка n удается только для, n=3,4 поэтому представляют большой интерес частные процедуры построения магических квадратов при n>4.Проще всего конструкция для магического квадрата нечетного порядка. Нужно в клетку с координатами (х,y) поставить число.

Ещё проще построение выполнить следующим образом, берется матрица n x n.Внутри её строится ступенчатый ромб. В нем ячейки слева вверх по диагоналям заполняются последовательным рядом чисел. Определяется значение центральной ячейки С.

Тогда в углах магического квадрата значения будут такими: верхняя правая ячейка С-1; нижняя левая ячейка С+1; нижняя правая ячейка С-n; верхняя левая ячейка С+n.

СОСТАВЛЕНИЕ МАГИЧЕСКИХ КВАДРАТОВ.

Каким же образом составляют магические квадраты?

Создание магического квадрата «Ло-Шу».

Задача : Квадрат 3х3, составить из цифр от 1 до 9, так, что бы суммы чисел в каждых строках, столбцах и по диагоналям были равны.

Решение: Решим задачу, не прибегая к перебору одной за другой всех перестановок 9 цифр в 9 клетках (число таких расстановок равно 362880). Будем рассуждать так. Сумма всех чисел от 1 до 9: 1+2+3+4+5+6+7+8+9=45. Значит, в каждой строке и в каждом столбце сумма чисел должна равняться: 45:3=15. Но если просуммировать все числа во-вторых столбце и строке и в обеих диагоналях, то каждое число войдёт один раз, за исключением центрального, которое войдёт четырежды. Значит, если обозначить центральное число через х, то должно выполняться равенство 4*15=3х+3*15. Отсюда х=5, то есть в центре таблицы должно стоять число 5.

Теперь заметим, что число 9 не может стоять в углу таблицы, скажем в левом верхнем углу. Ведь тогда в противоположном углу стояло бы число 1, а на первые строку и столбец оставалась бы одна комбинация — числа 4 и 2. Значит, 9 стоит в середине каких-то крайних строк или столбцов (у нас в середине первой строки). Двумя другими числами этой строки являются 4и2, а третьим числом среднего столбца должно быть 15-9-5=1. В одной строке с 1 должны стоять числа 8 и 6. Тем самым, магический квадрат почти заполнен и легко найти место для оставшихся чисел. В результате получается квадрат «Ло-Шу».

Конечно, для 9 можно выбрать другие три места, а после выбора места для этого числа остаются две возможности для расположения чисел 4 и 2. Всего получается 4*2=8 различных магических квадратов из трёх строк и трёх столбцов (или, как говорят математики, квадратов третьего порядка). Все эти квадраты можно получить на «Ло-Шу» либо поворачивая квадрат на 180,90 или 270. Еще возможен вариант зеркального отображения.

reshebniki-online.ru

Факультативное занятие по математике в 3-м классе: «Магические квадраты»

1. Научить заполнять магические квадраты.

2. Развивать наблюдательность, умение обобщать.

3. Прививать стремление к познанию нового, интерес к математике.

Оборудование: компьютер, мультимедиа проектор с экраном, презентация PowerPoint (Приложение 1).

В давние времена, научившись считать и выполнять арифметические действия, люди с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и таинственную. Складывая различные числа, располагая их друг за другом или одно под другим, они иногда получали одинаковую сумму. Наконец, разделив числа линиями так, чтобы каждое оказалось в отдельной клетке, увидели квадрат, любое из чисел которого принимало участие в двух суммах, а те, что расположены вдоль диагоналей – даже в трех, и все суммы равны между собой! Недаром древние китайцы, индусы, а вслед за ними и арабы приписывали таким конструкциям таинственные и магические свойства. (слайд 1)

Магические квадраты появились на Древнем Востоке еще до нашей эры. Одна из сохранившихся легенд повествует о том, что когда император Ю из династии Шан (2000 г до н.э.) стоял на берегу Ло, притоке Желтой реки, вдруг появилась большая рыба (в других вариантах – огромная черепаха), у которой на спине был рисунок из двух мистических символов – черных и белых кружочков (слайд 2), который был осознан затем как изображение магического квадрата порядка 3. (слайд 3)

Первое специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до 10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман. Их можно встретить на палубах больших пассажирских судов как площадку для игры.

Итак, под магическими будем понимать квадраты, в которых суммы чисел, стоящих в любом столбце или в любой строке, а также по диагоналям, одинаковы.

До сих пор вы использовали магические квадраты чаще всего для устного счета. При этом несколько чисел, в том числе и центральное, уже расставлены по клеткам квадрата. Требуется расставить остальные числа так, чтобы в любом направлении получилась определенная сумма.

Задача 1. Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Часть из них расставлена по клеткам Требуется расставить остальные числа, чтобы в сумме получалось 15. (слайд 4)

xn--i1abbnckbmcl9fb.xn--p1ai

Как решить магический квадрат (3 класс)? Пособия для школьников

Математических загадок существует невообразимое количество. Каждые из них уникальны по-своему, но их прелесть заключается в том, что для решения неизбежно нужно приходить к формулам. Конечно же, можно попытаться решить их, как говорится, методом тыка, но это будет очень долго и практически безуспешно.

В данной статье будет говориться об одной из таких загадок, а чтобы быть точнее — о магическом квадрате. Мы детально разберем, как решить магический квадрат. 3 класс общеобразовательной программы, конечно, это проходит, но возможно не каждый понял или вовсе не помнит.

Что это за загадка?

Магический квадрат, или, как его еще называют, волшебный, — это таблица, в которой число столбцов и строк одинаково, и все они заполнены разными цифрами. Главная задача, чтобы эти цифры в сумме по вертикали, горизонтали и диагонали давали одинаковое значение.

Помимо магического квадрата, есть еще и полумагический. Он подразумевает то, что сумма чисел одинакова лишь по вертикали и горизонтали. Магический квадрат «нормальный» только в том случае, если для заполнения использовались натуральные числа от единицы.

Еще есть такое понятие, как симметричный магический квадрат — это когда значение суммы двух цифр равно, в то время, когда они располагаются симметрично по отношению к центру.

Важно также знать, что квадраты могут быть любой величины помимо 2 на 2. Квадрат 1 на 1 также считается магическим, так как все условия выполняются, хотя и состоит он из одного-единственного числа.

Итак, с определением мы ознакомились, теперь поговорим про то, как решить магический квадрат. 3 класс школьной программы вряд ли все так детально разъяснит, как эта статья.

Какие есть решения

Те люди, которые знают, как решить магический квадрат (3 класс точно знает), сразу же скажут, что решения только три, и каждое из них подходит для разных квадратов, но все же нельзя обойти стороной и четвертое решение, а именно «наугад». Ведь в какой-то мере есть вероятность того, что незнающий человек все же сможет решить данную задачку. Но данный способ мы отбросим в длинный ящик и перейдем непосредственно к формулам и методикам.

Первый способ. Когда квадрат нечетный

Данный способ подходит только для решения такого квадрата, у которого количество ячеек нечетное, например, 3 на 3 или 5 на 5.

Итак, в любом случае изначально необходимо найти магическую константу. Это число, которое получится при сумме цифр по диагонали, вертикали и горизонтали. Вычисляется она с помощью формулы:

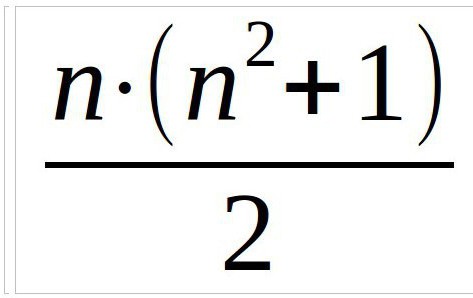
В данном примере мы рассмотрим квадрат три на три, поэтому формула будет выглядеть так (n — число столбцов):

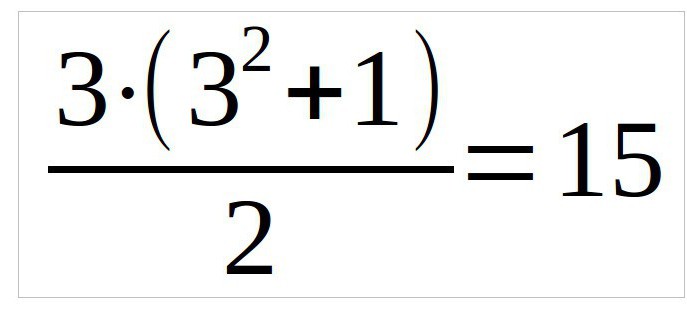
Итак, перед нами квадрат. Первое, что надо сделать — это вписать цифру один в центре первой строки сверху. Все последующие цифры необходимо располагать на одну клетку правей по диагонали.

Но тут сразу встает вопрос, как решить магический квадрат? 3 класс вряд ли использовал данный метод, да и у большинства появится проблема, как это сделать таким способом, если данной клетки нет? Чтобы сделать все правильно, необходимо включить воображение и дорисовать аналогичный магический квадрат сверху и получится так, что число 2 будет находиться в нем в нижней правой клетке. Значит, и в наш квадрат мы вписываем двойку в то же место. Это означает, что нам необходимо вписать цифры так, чтобы в сумме они давали значение 15.

Последующие цифры вписываются точно так же. То есть 3 будет находиться в центре первого столбца. А вот 4 по такому принципу вписать не удастся, так как на ее месте уже стоит единица. В таком случае цифру 4 располагаем под 3, и продолжаем. Пятерка — в центре квадрата, 6 — в правом верхнем углу, 7 — под 6, 8 — в верхний левый и 9 — по центру нижней строки.

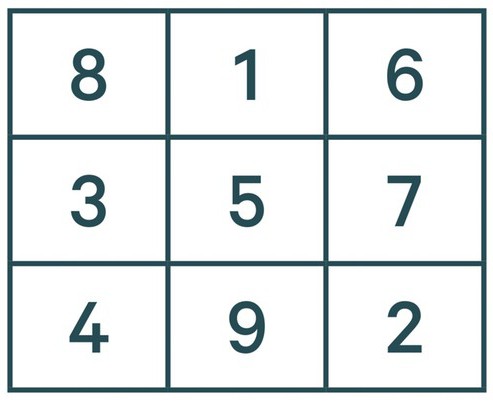
Вы теперь знаете, как решить магический квадрат. 3 класс Демидова проходил, но у этого автора были чуть попроще задания, однако, зная данный способ, удастся разгадать любую подобную задачу. Но это, если число столбцов нечетное. А что же делать, если у нас, например, квадрат 4 на 4? Об этом дальше по тексту.

Второй способ. Для квадрата двойной четности

Квадратом двойной четности называют тот, у которого количество столбцов можно разделить и на 2, и на 4. Сейчас мы рассмотри квадрат 4 на 4.

Итак, как решить магический квадрат (3 класс, Демидова, Козлова, Тонких — задание в учебнике математики), когда количество его столбцов равно 4? А очень просто. Проще, чем в примере до этого.

В первую очередь находим магическую константу по той же формуле, что приводилась в прошлый раз. В данном примере число равно 34. Теперь надо выстроить цифры так, чтобы сумма по вертикали, горизонтали и диагонали была одинаковой.

В первую очередь надо закрасить некоторые ячейки, сделать это вы можете карандашом или же в воображении. Закрашиваем все углы, то есть верхнюю левую клеточку и верхнюю правую, нижнюю левую и нижнюю правую. Если квадрат был бы 8 на 8, то закрашивать надо не одну клеточку в углу, а четыре, размером 2 на 2.

Теперь необходимо закрасить центр этого квадрата, так, чтобы его углы касались углов уже закрашенных клеточек. В данном примере у нас получится квадрат по центру 2 на 2.

Приступаем к заполнению. Заполнять будем слева направо, в том порядке, в котором расположены ячейки, только вписывать значение будем в закрашенные клетки. Получается, что в верхний левый угол вписываем 1, в правый — 4. Потом центральный заполняем 6, 7 и дальше 10, 11. Нижний левый 13 и правый — 16. Думаем, порядок заполнения понятен.

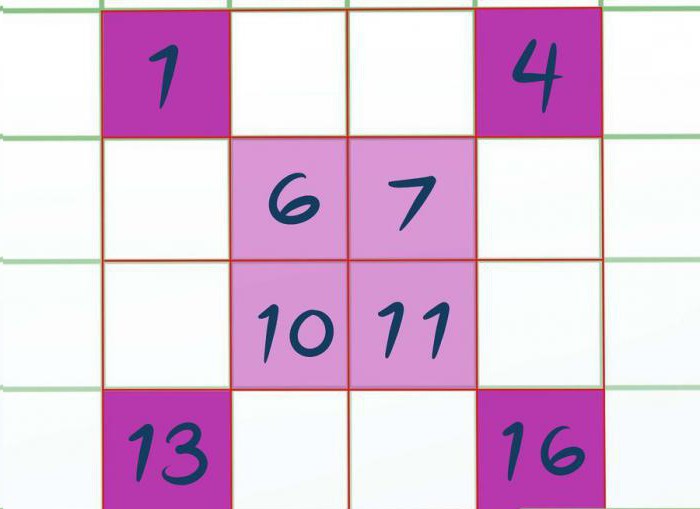
Остальные ячейки заполняем точно так же, только в порядке убывания. То есть так как последняя вписанная цифра была 16, то вверху квадрата пишем 15. Далее 14. Потом 12, 9 и так далее, как показано на картинке.

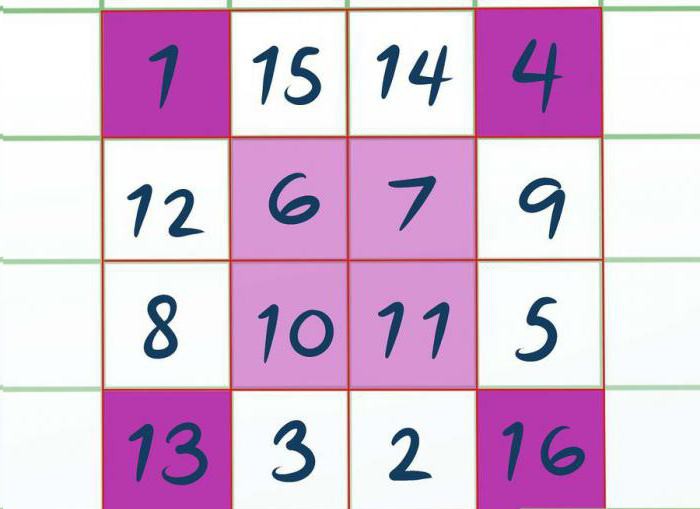
Теперь вы знаете второй способ, как решить магический квадрат. 3 класс согласится, что квадрат двойной четности намного легче решается, чем другие. Ну а мы переходим к последнему способу.

Третий способ. Для квадрата одинарной четности

Квадратом одинарной четности называется, тот квадрат, число столбцов которого можно разделить на два, но нельзя на четыре. В данном случае это квадрат 6 на 6.

Итак, вычисляем магическую константу. Она равна 111.

Теперь нужно наш квадрат визуально поделить на четыре разных квадрата 3 на 3. Получится четыре маленьких квадрата размером 3 на 3 в одном большом 6 на 6. Верхний левый назовем А, нижний правый — В, верхний правый — С и нижний левый — D.

Теперь необходимо каждый маленький квадрат решить, используя самый первый способ, что приведен в этой статье. Получится так, что в квадрате А будут числа от 1 до 9, в В — от 10 до 18, в С — от 19 до 27 и D — от 28 до 36.

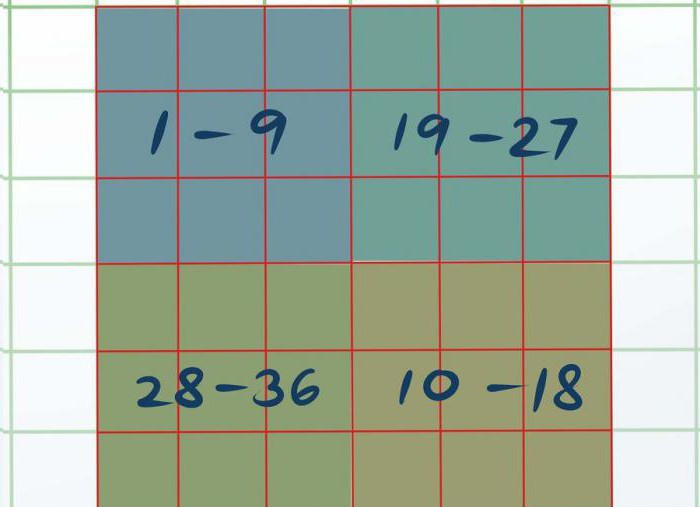
Как только вы решили все четыре квадрата, работа начнется над А и D. Необходимо в квадрате А визуально или при помощи карандаша выделить три ячейки, а именно: верхнюю левую, центральную и нижнюю левую. Получится так, что выделенные цифры — это 8, 5 и 4. Точно так же надо выделить и квадрат D (35, 33, 31). Все, что остается сделать, это поменять местами выделенные цифры из квадрата D в А.

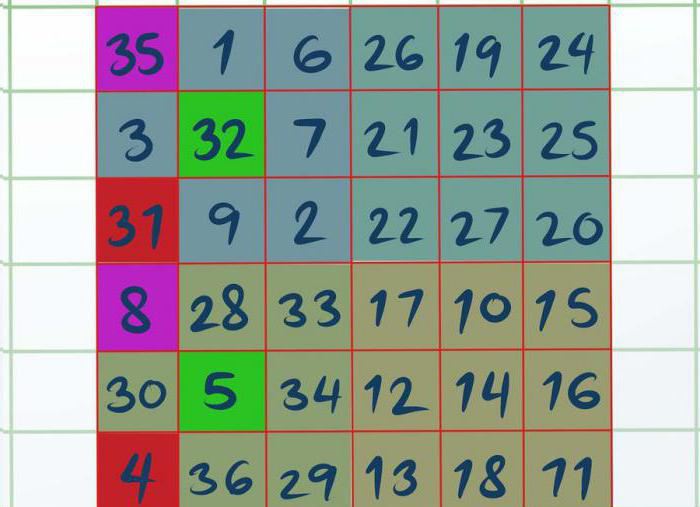
Теперь вы знаете последний способ, как можно решить магический квадрат. 3 класс квадрат одинарной четности не любит больше всего. И это неудивительно, из всех представленных он самый сложный.

Прочтя данную статью, вы узнали, как решить магический квадрат. 3 класс (Моро — автор учебника) предлагает подобные задачи только с несколькими заполненными ячейками. Рассматривать его примеры нет смысла, так как зная все три способа, вы с легкостью решите и все предлагаемые задачи.

fb.ru