Закон изменения эдс со временем

Лабораторная работа

ЛАБОРАТОРНАЯ РАБОТА № 2.10

ИЗУЧЕНИЕ ЯВЛЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Экспериментально изучить частные случаи основного закона электромагнитной индукции.

2.10.2 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Явление электромагнитной индукции состоит в том, что при изменении магнитного потока через поверхность, ограниченную контуром, в последнем возбуждается электродвижущая сила индукции. Если проводящий контур замкнутый, то под действием этой ЭДС в нем возникает электрический ток, называемый индукционным. Согласно закону Ленца, индукционный ток всегда имеет такое направление, что его магнитное поле противодействует изменению магнитного потока.

Магнитный поток Ф сквозь поверхность, ограниченную произвольным замкнутым контуром, может изменяться по ряду причин: за счет изменения геометрии контура, изменения его расположения в магнитном поле, вследствие зависимости магнитной индукции от времени. Согласно закону Фарадея, электродвижущая сила индукции, возникающая в контуре, численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром:

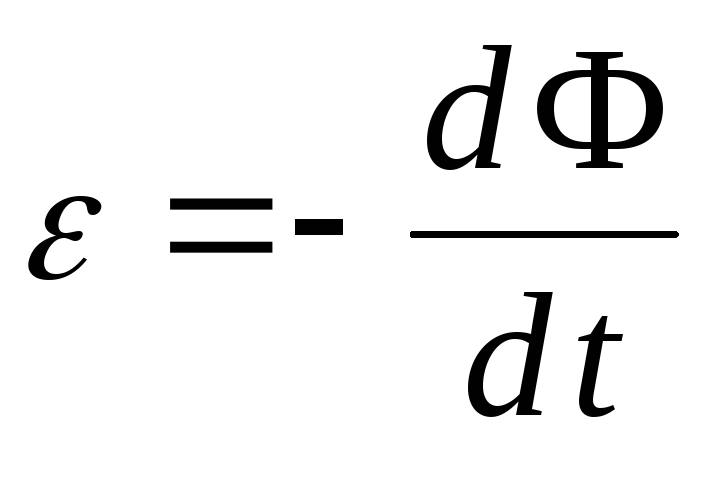. (2.10.1)

Уравнение (2.10.1) выражает основной закон электромагнитной индукции в общем виде.

Рассмотрим контур, состоящий из N витков, в котором индуцируется ЭДС. Поскольку витки соединяются последовательно, ЭДС, возбуждаемые в отдельных витках, будут складываться. Поэтому

Величину называют потокосцеплением или полным магнитным потоком. Если потоки Ф_i, пронизывающие каждый из витков, одинаковы, то . Отсюда

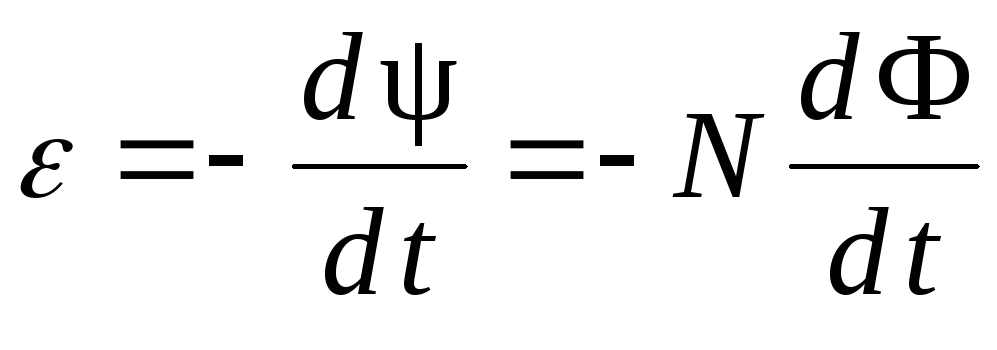. (2.10.2)

Хотя величина ЭДС индукции не зависит от способа изменения магнитного потока, однако механизм ее возникновения при этом оказывается разным. Обратимся сначала к случаю, когда поток изменяется вследствие движения проводящего контура (или изменения его геометрии) в постоянном магнитном поле. Здесь роль сторонних сил, разделяющих разноименные заряды в проводнике, играет магнитная составляющая силы Лоренца

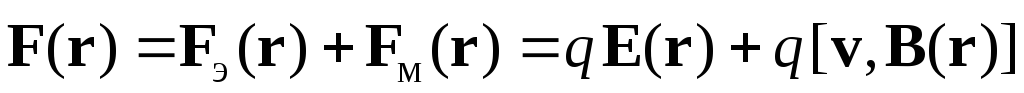Если неподвижный проводник находится в изменяющемся со временем магнитном поле, то механизм возникновения ЭДС оказывается другим. Изменяющееся магнитное поле возбуждает вихревое электрическое поле, под действием которого носители заряда приходят в движение. Таким образом, в неподвижном контуре возникает ЭДС индукции

Собственное магнитное поле проводника с током I создает полный поток 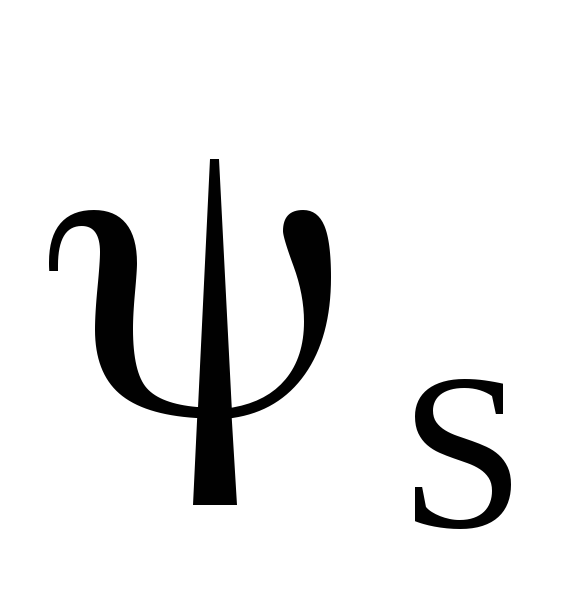через поверхность, ограниченную этим проводником. Согласно закону Био-Савара-Лапласа, индукция поляB пропорциональна току I. Значит, величины 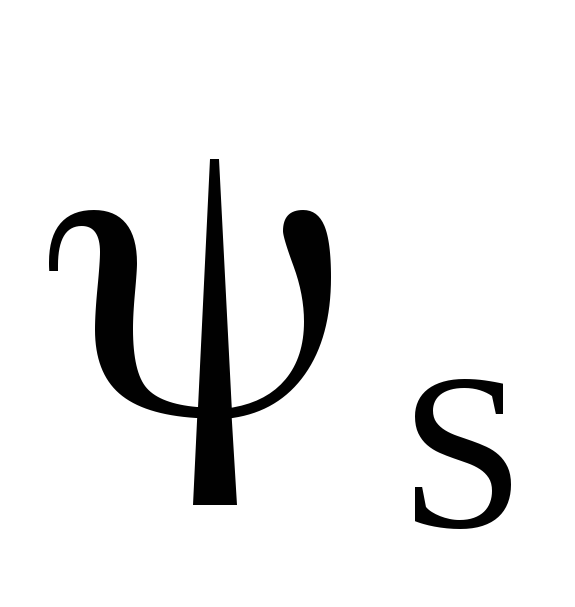иI тоже пропорциональны друг другу, т.е.

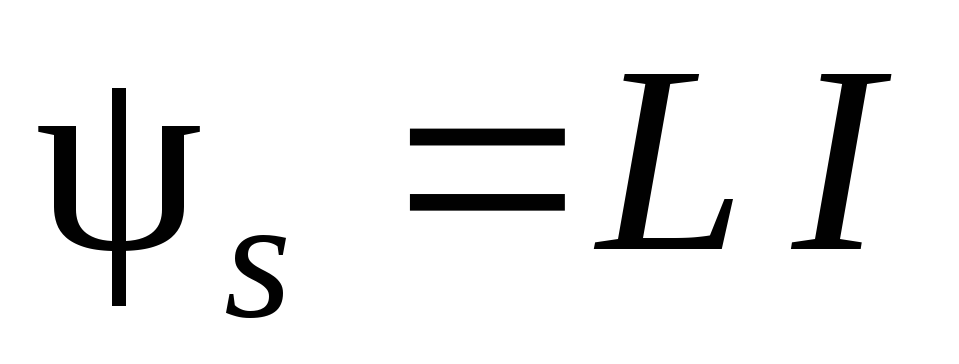,(2.10.3)

где L  индуктивность проводника. Величина L зависит от геометрии контура (т.е. от его формы и размеров), а также от магнитных свойств среды, в которой он находится, характеризуемых проницаемостью . Однако если среда ферромагнитная, то  является сложной функцией от тока. Значит, индуктивность проводника оказывается зависящей от величины тока. Формула (2.10.3) остается справедливой и для такого случая.

Если ток в контуре изменяется каким-либо образом, то это приводит к изменению собственного потока . В результате в контуре возбуждается ЭДС, называемая электродвижущей силой самоиндукции . Из выражений (2.10.2) и (2.10.3) следует, что

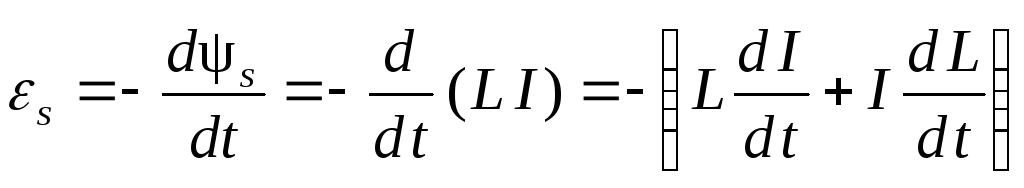Если среда неферромагнитная и контур не деформируется, то L = const и

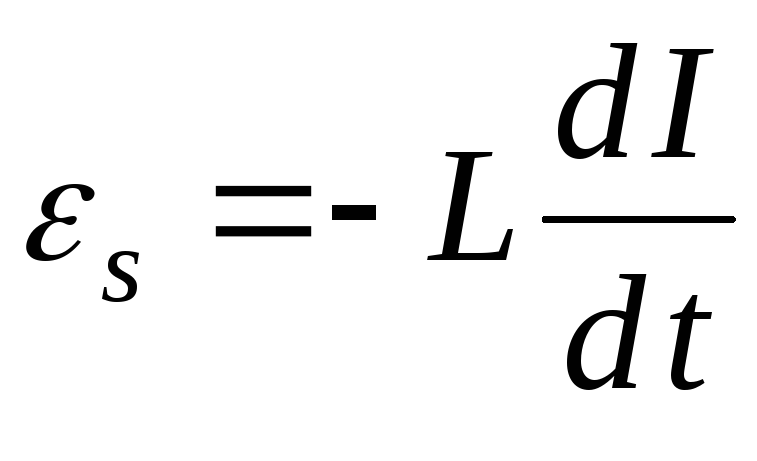Под действием ЭДС самоиндукции возникает индукционный ток, который по закону Ленца противодействует изменению тока в цепи: замедляет его возрастание или убывание.

Рассмотрим два контура, расположенных близко друг к другу (рис.2.10.1).

При прохождении электрического тока I₁ по контуру 1 в каждой точке пространства создается магнитное поле. Индукция этого поля пропорциональна току I₁. Поэтому магнитный поток через поверхность, ограниченную контуром 2, также пропорционален I₁: , где коэффициент пропорциональности L₂₁ называется коэффициентом взаимной индукции. При изменении тока I₁ меняется также магнитный поток ₂₁ и в контуре 2 индуцируется ЭДС:

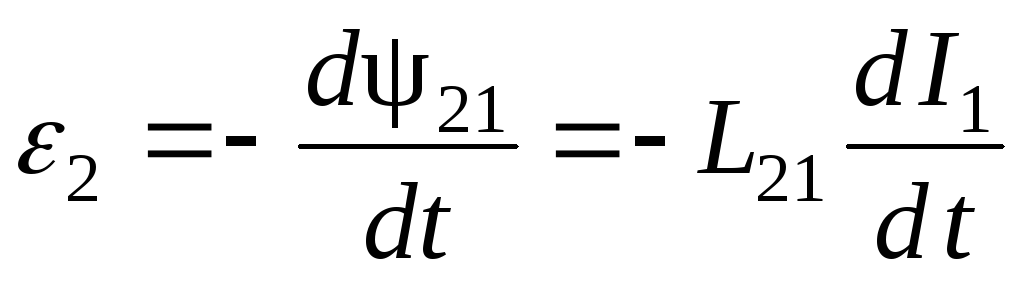Аналогично при протекании в контуре 2 тока I₂ создается магнитное поле и поверхность, ограниченную контуром 1, пронизывает магнитный поток 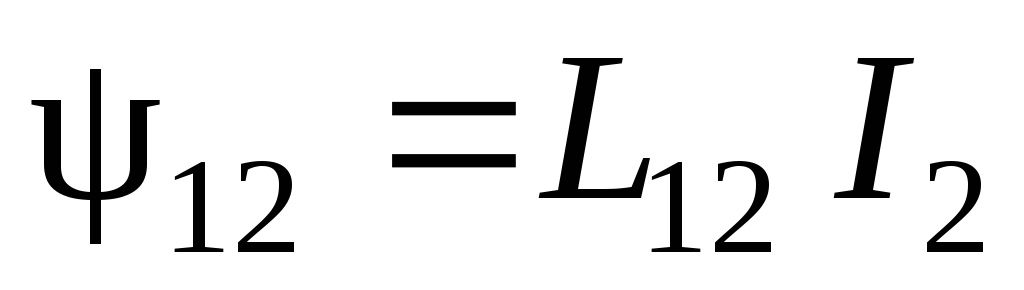. При изменении тока I₂ индуцируется ЭДС в контуре 1:

Говорят, что между этими контурами существует магнитная связь, само же явление возникновения ЭДС в одном из проводников вследствие изменения тока в другом называют взаимной индукцией. Коэффициенты L₁₂ и L₂₁ называются коэффициентами взаимной индукции. Их величина зависит от формы, размеров и взаимного расположения проводников, а также от магнитной проницаемости среды. В отсутствие ферромагнетиков L₁₂ = L₂₁. На явлении взаимной индукции основано действие трансформаторов.

В работе предлагается проверить на опыте некоторые частные случаи явления электромагнитной индукции. Схема установки приведена на рис. 2.10.2. Изменяющееся магнитное поле в длинном соленоиде L₀ возбуждает вихревое электрическое поле, под действием которого носители заряда в катушках L₁  L₅ приходят в движение.

Таким образом, в этих катушках возникает ЭДС индукции, амплитудное значение которой измеряется электронным осциллографом (рис.2.10.2.). Кнопочный переключатель (П) дает возможность подключить одну из секций L₁  L₅ (число витков в каждой секции катушки одинаково).

Согласно закону электромагнитной индукции

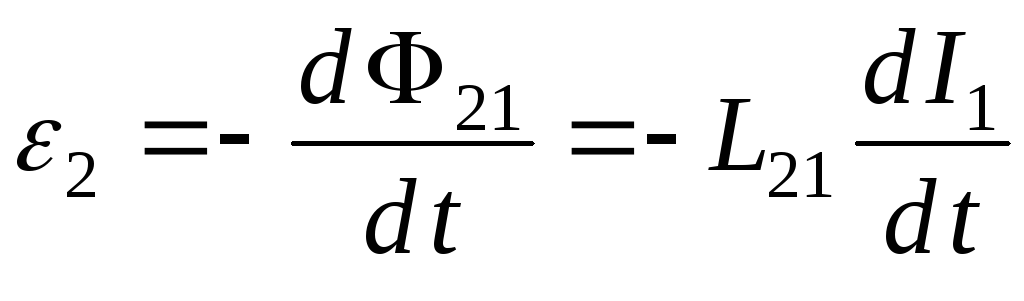где ₂  ЭДС индукции, возникающая во вторичной катушке; Ф₂₁  магнитный поток пронизывающий вторичную катушку; I₁ – ток, текущий в первичной катушке и создающий магнитное поле.

Так как в катушке L₀ течет переменный ток I₁, изменяющийся по закону

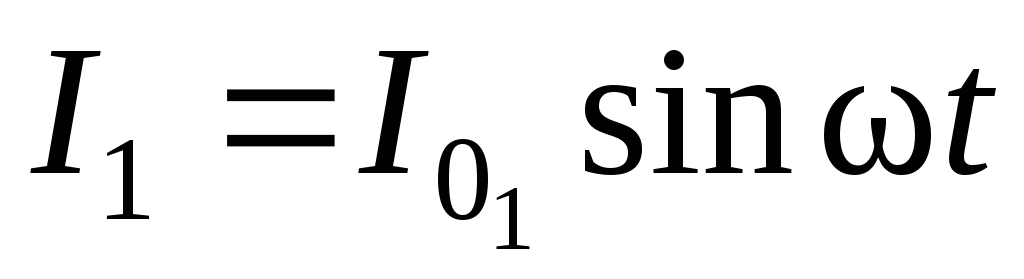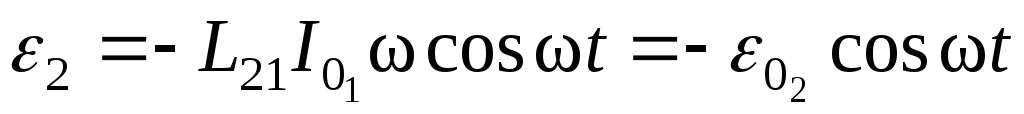Амплитудное значение тока во вторичной цепи

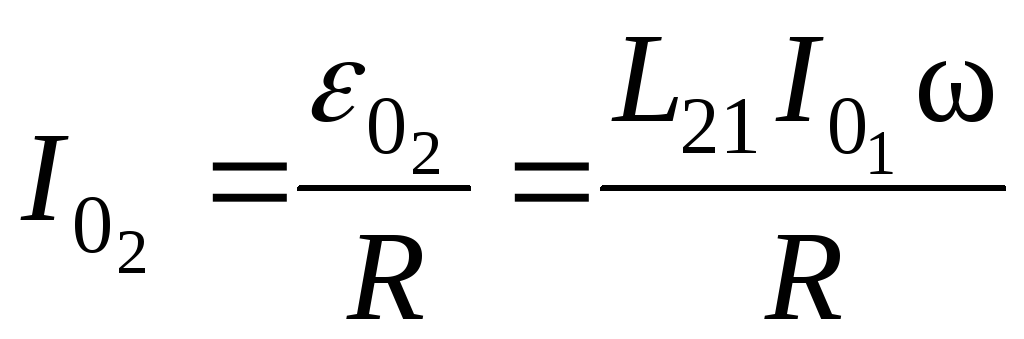где R  сопротивление вторичной цепи.

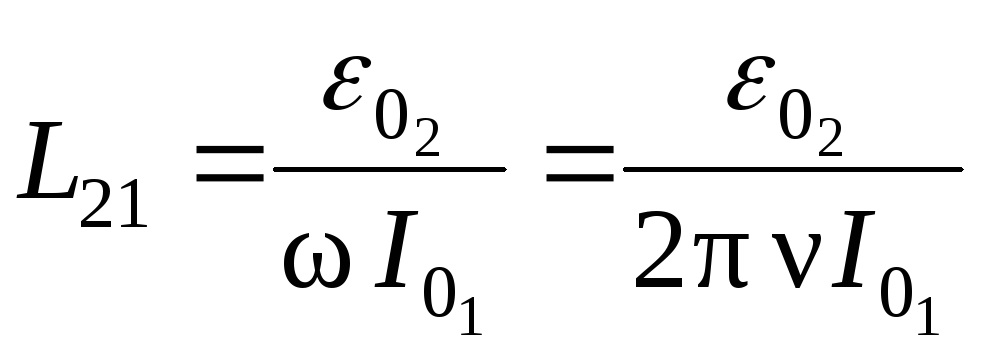, (2.10.4)

где 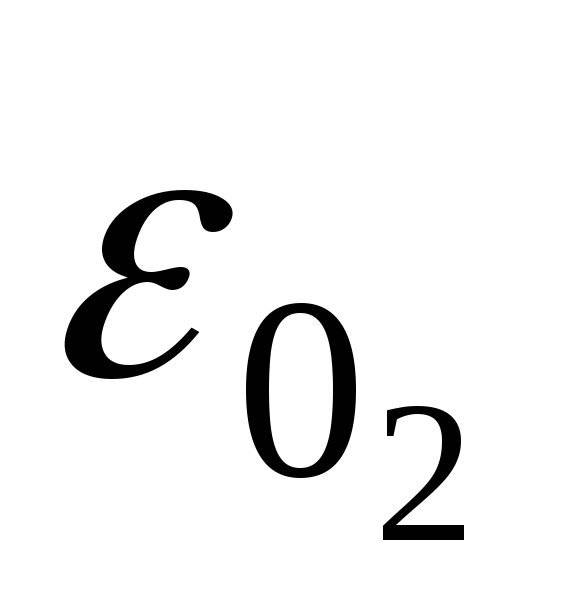 ЭДС, определяемая с помощью осциллографа.

Наличие переключателя «Гн, Осц.» дает возможность катушкам поменяться ролями (рис. 2.10.3). Звуковой генератор (ЗГ) подключается к одной из катушек L₁  L₅, а осциллограф к соленоиду L₀. При этом коэффициент взаимной индукции находят по формуле

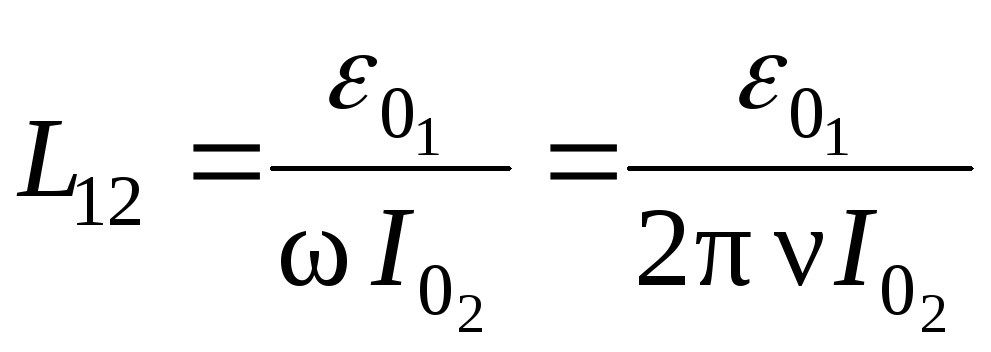. (2.10.5)

Рассчитав коэффициент взаимной индукции, легко убедиться в справедливости формулы

. (2.10.6)

studfiles.net

Закон изменения эдс со временем

§3. Закон электромагнитной индукции. Правило Ленца

Пусть произвольный контур с током находится во внешнем магнитном поле. Из принципа суперпозиции магнитных полей и определения магнитного потока следует, что полный магнитный поток `»Ф»`, пронизывающий контур, состоит из потока от внешнего поля `»Ф»_»внеш»` и потока от собственного поля `»Ф»_»соб»`:

При этом внешний магнитный поток `»Ф»_»внеш»` может изменяться со временем как из-за изменения внешнего магнитного поля во времени (в каждой точке поля индукция внешнего магнитного поля зависит от времени), так и из-за движения контура или отдельных его частей. Собственный магнитный поток `»Ф»_»соб»` может тоже меняться со временем в результате изменения тока в контуре по каким-либо причинам и в результате изменения индуктивности контура (при его деформации, например).

Опытным путём установлено, что независимо от причин, вызывающих изменение полного магнитного потока через контур, в контуре возникает электродвижущая сила, называемая электродвижущей силой индукции:

`=-(d»Ф»)/(dt)`. (4)

Здесь направление нормали к контуру и положительное направление обхода контура, связанные друг с другом правилом буравчика, определяют знак `»Ф»` и ЭДС индукции положительна, если направление её действия совпадает с положительным направлением обхода контура, и отрицательна в противном случае. Под направлением действия ЭДС на некотором участке цепи будем понимать направление действия вдоль этого участка сторонних сил на положительные заряды, т. е. то направление, в котором потечёт ток через участок цепи с ЭДС при мысленном замыкании этого участка резистором.

Равенство (4) и представляет собой математическую запись закона электромагнитной индукции Фарадея. Производную `(d»Ф»)/(dt)` называют скоростью изменения магнитного потока.

Из равенств (3) и (4) получаем:

`=-(d»Ф»_»внеш»)/(dt)-(d»Ф»_»соб»)/(dt)`. (5)

Слагаемое `-(d»Ф»_»внеш»)/(dt)` представляет собой ЭДС индукции, возникающую из-за изменения внешнего магнитного потока. Если собственное поле можно не учитывать (пренебрегать индуктивностью), то ЭДС индукции в контуре определяется только первым слагаемым. Ещё раз подчеркнём, что это слагаемое обусловлено как изменением внешнего поля во времени, так и движением контура или его частей во внешнем поле.

`=-(d»Ф»_»соб»)/(dt)=-(d(LI))/(dt)=-L(dI)/(dt)-I(dL)/(dt)` (6)

называется ЭДС самоиндукции, т. к. оно появляется благодаря изменению во времени собственного магнитного потока через контур. Напомним, что изменение собственного магнитного потока может происходить как за счёт изменения тока (по каким-либо причинам), так и за счёт изменения индуктивности контура.

Если индуктивность остаётся постоянной во времени, то равенство (6) принимает вид:

`=-L(dI)/(dt)`. (7)

Затронем часто встречающийся при решении задач вопрос о том, пренебрегать или нет индуктивностью контура. Этот вопрос в каждом конкретном случае должен решаться отдельно на основании вклада, даваемого в общую ЭДС каждым слагаемым в формуле (5). Чаще всего индуктивностью контура в виде одного витка или рамки, состоящей из малого числа витков, можно пренебречь. А вот индуктивностью контура, состоящего из значительного числа витков, например катушки, пренебрегать не стоит. Одним из критериев для оценки роли индуктивности может служить сравнение величин внешнего магнитного поля и собственного поля контура, а точнее, сравнение изменений величин этих полей за время наблюдения.

Заметим, что в формуле (4) знаки ЭДС индукции и изменения магнитного потока `d»Ф»` противоположны: если `d»Ф»>0`, то `

zftsh.online

Глава 23. Закон электромагнитной индукции

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м 2 однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3).

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).