Справедлив ли закон архимеда в невесомости

Архимед — величайший древнегреческий ученый, математик, физик, изобретатель, родился в 287г. до н.э. в Сиракузах на острове Сицилия. Он прославился многочисленными научными трудами, главным образом в области геометрии и механики. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку.

Существует легенда об открытии «закона Архимеда», связанная с золотой короной царя Сиракуз Гиероном II.
Историки считают, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Результатом было появление замечательного сочинения «О плавающих телах», которое дошло до наших дней.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Закон Архимеда справедлив только при наличии тяжести. В условиях невесомости он не выполняется.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:

Fт>FA — тело тонет;

Fт=FA — тело плавает в жидкости или газе;

Fт F_A — тело тонет;

F_т=F_A — тело плавает в жидкости или газе;
F_т >V_г, то выталкивающая сила F_ш, действующая на шар, значительно больше выталкивающей силы V_г, действующей на гирю. Поэтому наблюдаемое в воздухе равновесие шара и гири не означает одинаковости их весов в пустоте. На самом деле истинный вес шара P_ш больше истинного веса гири P_г. Это сразу обнаруживается, когда из-под колокола насоса откачивают воздух. Весы выходят из равновесия, шар опускается вниз. Таким образом, данный опыт наглядно показывает справедливость закона Архимеда и для газов.

На использовании действия архимедовой силы в газах основано воздухоплавание — полеты дирижаблей, аэростатов и т. п.

Механическая работа. Мощность

Механическая работа

Если действующая на тело сила F вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).

Механической работой А называют скалярную величину, равную произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы, т. е.

В случае, описываемом формулой (3.9), направление перемещения тела совпадает с направлением силы. Однако чаще встречаются случаи, когда сила и перемещение составляют между собой угол, не равный нулю или . (рис. 30)

Разложим силу F на две взаимно перпендикулярные составляющие F₁ и F₂ (F=F₁+F₂). Поскольку механическая работа — величина скалярная, то работа силы F равна алгебраической сумме работ сил F₁ и F₂, т. е. А=А₁+А₂.

Под действием силы F₂ тело перемещения не совершает, так как F₂s. Поэтому A₂=0. Следовательно, работа А=А₁=F₁s. Из рисунка видно, что F₁=Fcos. Поэтому

Таким образом, в общем случае механическая работа равна произведению модуля силы и модуля перемещения на косинус угла между направлениями силы и перемещения. Работа силы, направленной вдоль перемещения тела, положительна, а силы, направленной против перемещения тела, — отрицательна. По формулам (3.9) и (3.10) вычисляют работу постоянной силы. Единицу механической работы устанавливают из формулы (3.9). В СИ за единицу работы принята работа силы 1 Н при перемещении точки ее приложения на 1 м. Эта единица имеет наименование джоуль (Дж):
1 Дж = 1Н·1м.

Из формулы (3.11) следует, что в СИ единицей мощности яв-ляется 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.

Связь между мощностью и скоростью при равномерном движении найдем, подставив (3.10) в (3.11):

(Эта формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V — мгновенную скорость). Если направление силы совпадает с направлением перемещения, то cos=1 и N=Fv. Из последней формулы следует, что

Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.

Применение простых механизмов

Рычаг в физике — простой механизм

Различают два вида рычагов. У рычага первого рода точка опоры находится между линиями действия приложенных сил. У рычага второго рода точка опоры расположена по одну сторону от них. То есть, если мы пытаемся при помощи лома сдвинуть с места тяжелый предмет, то рычаг первого рода – это ситуация, когда мы подкладываем брусок под лом, надавливая на свободный конец лома вниз. Неподвижной опорой у нас в данном случае будет являться брусок, а приложенные силы располагаются по обе стороны от него. А рычаг второго рода – это когда мы, подсунув край лома под тяжесть, тянем лом вверх, пытаясь таким образом перевернуть предмет. Здесь точка опоры находится в месте упора лома о землю, а приложенные силы расположены по одну сторону от точки опоры.

Закон равновесия сил на рычаге

где F1 и F2 – силы, действующие на рычаг,
а l2 и l1 – плечи этих сил.

Это и есть закон равновесия рычага, который гласит: рычаг находится в равновесии тогда, когда действующие на него силы обратно пропорциональны плечам этих сил. Этот закон был установлен Архимедом еще в третьем веке до нашей эры. Из него следует, что меньшей силой можно уравновесить большую. Для этого необходимо, чтобы плечо меньшей силы было больше плеча большей силы. А выигрыш в силе, получаемый с помощью рычага, определяется отношением плеч приложенных сил.

Начав использоваться с глубокой древности, рычаг повсеместно применяется и в наши дни, как на производстве, например, подъемные краны, так и в быту, например, ножницы, весы и так далее.

Приложение закона равновесия

Блок представляет собой устройство, которое состоит из колеса с желобом, по которому пропускают, трос, веревку или цепь, а также прикрепленной к оси колеса обоймы с крюком. Блок может быть неподвижным и подвижным. У неподвижного блока ось закреплена, и она не двигается при подъеме или опускании груза. Неподвижный блок помогает изменить направление действия силы. Перекинув через такой блок, подвешенный вверху, веревку, мы можем, поднимать груз вверх, сами при этом находясь внизу. Однако выигрыша в силе применение неподвижного блока нам не дает. Мы можем представить блок в виде рычага, вращающегося вокруг неподвижной опоры – оси блока. Тогда радиус блока будет равен плечам, приложенных с двух сторон сил, – силы тяги нашей веревки с грузом с одной стороны и силы тяжести груза с другой. Плечи будут равны, соответственно, выигрыша в силе нет.

Иначе обстоит дело с подвижным блоком. Подвижный блок перемещается вместе с грузом, он как бы лежит на веревке. В таком случае точка опоры в каждый момент времени будет находиться в месте соприкосновения блока с веревкой с одной стороны, воздействие груза будет приложено к центру блока, где он и крепится на оси, а сила тяги будет приложена в месте соприкосновения с веревкой с другой стороны блока. То есть плечом веса тела будет радиус блока, а плечом силы нашей тяги – диаметр. Диаметр, как известно, в два раза больше радиуса, соответственно, плечи различаются по длине в два раза, и выигрыш в силе, получаемый с помощью подвижного блока, равен двум. На практике применяют комбинацию неподвижного блока с подвижным. Закрепленный вверху неподвижный блок не дает выигрыша в силе, однако помогает поднимать груз, стоя внизу. А подвижный блок, перемещаясь вместе с грузом, увеличивает прикладываемую силу вдвое, помогая поднимать большие грузы на высоту.

Золотое правило механики

Равенство работ при использовании простых механизмов

Мы видим, что с помощью простых механизмов можно получить выигрыш в силе. А дают ли простые механизмы выигрыш в работе?

Рассчитаем работу, которую совершает сила F при подъеме груза с помощью наклонной плоскости (см. рис. 1):

Подставим найденные значения силы и получим

Таким образом, работа A_F равна работе, которую нужно совершить, чтобы равномерно поднять груз на высоту h, не используя наклонной плоскости.

При использовании неподвижного блока мы видим, что приложенные силы F и mg равны и пути, пройденные точками приложения сил при подъеме груза, тоже одинаковы, а значит, одинаковы и работы.

Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому приложена сила F, переместить на 2h. Следовательно, A₁ = mgh и .

Таким образом, получая выигрыш в силе в два раза, проигрывают в два раза в перемещении, следовательно, и подвижный блок выигрыша в работе не дает.

Многовековая практика показала, что ни один из простых механизмов не дает выигрыша в работе.

Еще древние ученые сформулировали правило («золотое правило механики»), применяемое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии.

При рассмотрении простых механизмов мы не учитываем трение, а также вес самих механизмов. В реальных условиях это необходимо учитывать. Поэтому часть работы совершается силой F на перемещение отдельных частей механизма и против силы трения. Работа же по подъему груза A_p (полезная работа) будет меньше полной работы А (работы, которую совершает сила F).

Эффективность работы механизма характеризуют коэффициентом полезного действия (КПД механизма):

Коэффициент полезного действия — физическая величина, равная отношению полезной работы A_p ко всей затраченной работе А:

Работа совершённая, приложенной силой называется полной работой. Полезной работой является работа по подъёму груза или преодоления какого-либо сопротивления. На практике полная работа всегда больше полезной работы. Часть работы совершается против сил трения в механизме и по перемещению его отдельных частей. Так, поднимая груз с помощью подвижного блока, приходится совершать работу по подъему не только груза, но и самого блока, веревки, совершать работу по преодолению сил трения в оси блока.

Какой бы механизм мы не взяли, полезная работа, совершённая с его помощью, всегда будет составлять лишь часть полной работы.

Отношение полезной работы к полной работе называют коэффициентом полезного действия. (Сокращённо обозначают коэффициент полезного действия КПД).

где А_п – полезная работа, А – полная работа. КПД обычно выражают в процентах.

КПД любого механизма всегда меньше единицы, так как А_п (полезная работа) всегда меньше чем А (полная работа).

nenuda.ru

Тест «Физика и космос»

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Электронный тест «Физика и космос»

Справедливы ли законы Паскаля и Архимеда внутри космического корабля, находящегося в свободном полёте?

1) справедлив только закон Архимеда;

2) справедлив только закон Паскаля;

3) справедливы оба закона. В условиях невесомости сила Архимеда

равна силе тяжести;

4) справедливы оба закона. В условиях невесомости сила Архимеда равна нулю.

Совершают ли космонавты работу при перемещении грузов в невесомости?

1) работа совершается в начале и конце движения груза, когда он

2) работа совершается в начале движения груза;

3) работа совершается при перемещении грузов в невесомости, когда

груз движется равномерно;

4) работа при перемещении груза в невесомости не совершается.

3. На каких этапах полёта космонавт имеет наибольший вес?

1) на этапе взлёта, когда космический корабль движется

2) на этапах взлёта и посадки, когда космический корабль движется

3) на этапе посадки, когда космический корабль движется

с ускорением, имеет место перегрузка;

4) на этапах взлёта и посадки, когда космический корабль движется

равномерно, имеет место перегрузка.

Почему спускаемые отсеки пилотируемых космических кораблей

покрывают слоем керамики?

1) При движении спускаемого аппарата в плотных слоях атмосферы его

поверхность нагревается до высокой температуры;

2) Керамика обладает малой теплопроводностью и большой удельной

3) При движении спускаемого аппарата в плотных слоях атмосферы его

поверхность нагревается до высокой температуры. Керамика обладает

большой теплопроводностью и большой удельной теплотой плавления;

4) При движении спускаемого аппарата в плотных слоях атмосферы его

поверхность нагревается до высокой температуры. Керамика обладает малой

теплопроводностью и большой удельной теплотой плавления.

5. Почему высота полётов пилотируемых космических кораблей не превышает

1) выше 300 км располагаются радиационные пояса Земли, пролетая через

которые космонавты могут приобрести лучевую болезнь и даже погибнуть;

2) выше 300 км располагаются радиационные пояса Земли;

3) не позволяет мощность космического корабля;

4) выше 300 км в космическом пространстве находится вакуум.

6. Почему на внешней поверхности корабля, находящегося долгое время на орбите,

происходит сваривание металлических деталей?

1) в вакууме происходит холодная сварка металлических деталей;

2) в вакууме вследствие диффузии происходит холодная сварка металлических

3) оказывает влияние невесомость;

4) оказывает влияние большая скорость космического корабля.

7. Почему топливо космической ракеты обязательно состоит из двух компонентов,

например водорода и кислорода, в то время как топливо реактивного самолёта

1) в двигателях, работающих на Земле, окислителем горючего является

2) в космической ракете, работающей в условиях

вакуума, топливо должно состоять из двух компонентов: горючего и

3) в двигателях, работающих на Земле, окислителем горючего является

атмосферный кислород. В космической ракете, работающей в условиях

4) в двигателях, работающих на Земле, окислителем горючего является

вакуума, топливо должно содержать кислород.

8. Почему современные космические ракеты состоят из нескольких ступеней?

1) Идея многоступенчатых ракет – «ракетных поездов» — была выдвинута

К. Э. Циолковским. При последовательном сбрасывании частей корпуса

2) Идея многоступенчатых ракет – «ракетных поездов» — была выдвинута

С.П. Королевым. При последовательном сбрасывании частей корпуса

ракеты происходит существенная экономия топлива.

9. Какая планета является двойником Земли?

10. Какая планета могла бы называться планетой Океан?

Таблица ответов на Электронный тест «Физика и космос»

Тест «Физика и космос» был составлен для закрепления знаний физических законов, которые встречаются и учитываются при полетах в космическое пространство. Данный тест можно использовать при проведении декады физики, математики и информатики посвященной «Дню космонавтики и авиации». Первые полеты в космическое пространство, первый полет человека в космос показали, что в космосе человек испытывает как перегрузки, так и невесомость. Когда космонавт испытывает перегрузки? Что такое невесомость? Почему высота полётов пилотируемых космических кораблей не превышает 300 км? Почему современные космические ракеты состоят из нескольких ступеней?
- Гринева Мария Николаевна
- 742
- 19.04.2015
Номер материала: 488647

Свидетельство о публикации данного материала автор может скачать в разделе «Достижения» своего сайта.

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

infourok.ru

ДЗ — Сила Архимеда. (5)

Внимание. обнаружен плагиат. Источник

Формулировка и пояснения

Закон Архимеда формулируется следующим образом[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная силе тяжести вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:

$ _A = \rho V, $ где $ \rho $ — плотность жидкости (газа), $ $ — ускорение свободного падения, а $ V $ — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

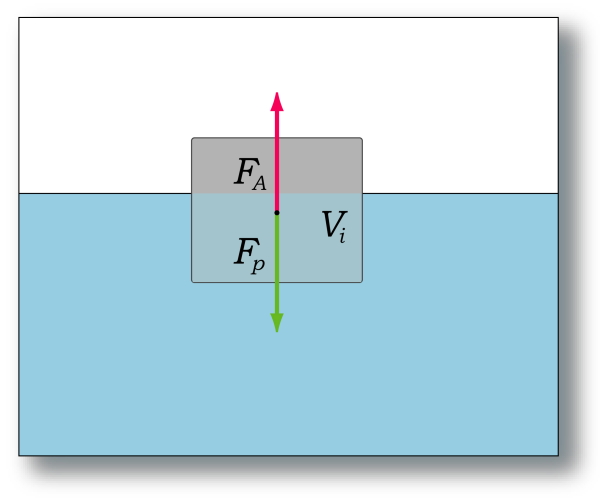
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела. $ P_B-P_A = \rho g h F_B-F_A = \rho g h S = \rho g V, $ где $ PA $ , $ PB $ — давления в точках A и B, $ ρ $ — плотность жидкости, $ h $ — разница уровней между точками $ A $ и $ B $ , $ S $ — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.

В теоретической физике также применяют закон Архимеда в интегральной форме: $ _A = \iint\limits_S

>, $ где $ S $ — площадь поверхности, $ p $ — давление в произвольной точке, интегрирование производится по всей поверхности тела.

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление жидкости на глубине $ h $ есть $ p = \rho g h $ . При этом считаем плотность жидкости и напряжённость гравитационного поля постоянными величинами, а $ h $ — параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат $ Oxyz $ , причём выберем направление оси $ z $ совпадающим с направлением вектора $ \vec $ . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку $ dS $ . На неё будет действовать сила давления жидкости направленная внутрь тела, $ d\vec_A = -pd\vec ~~$ . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности: $ \vec_A=-\int\limits_S~~

~~>=-\int\limits_S<\rho g h \,d\vec~~>=-\rho g\int\limits_S>=^*-\rho g\int\limits_V=^<**>-\rho g\int\limits_V<\vec_zdV>=-\rho g \vec_z \int\limits_V = (\rho g V) (-\vec_) $ При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса (очень смешно, правда. классная теорема, в первом классе проходил ). $ <>^* h(x,y,z) = z; \quad ^ <**>grad(h)=\nabla h=\vec_ $ Получаем, что модуль силы Архимеда равен $ \rho g V $ , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.

~~Условие плавания тел~~

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести $ \mathbf $ и силы Архимеда $ \mathbf_A $ , которые действуют на это тело. Возможны следующие три случая: $ \mathbf>\mathbf_A $ — тело тонет; $ \mathbf=\mathbf_A $ — тело плавает в жидкости или газе; $ \mathbf \mathbf

~~_s $ — тело тонет; $ \mathbf=\mathbf~~

~~_s $ — тело плавает в жидкости или газе; $ \mathbf Поиск~~

~~conspectus.theschool.spb.ru~~

~~Исследование границ применимости закона Архимеда~~

Закон Архимеда очень хорошо известен всем, кто посещал школу. Но на первый взгляд такой простой и понятный закон имеет свои » тайны», При изучении законов не может быть мелочей и выяснение границ применимости – тоже очень важно. Эти знания помогут понять, где и как можно применять тот или иной закон, расширят кругозор.

~~Выполняя данную работу можно сделать следующие выводы:~~

~~Предварительный просмотр:~~

~~МОУ Краснореченская ООШ~~

~~Исследование границ применимости закона Архимеда~~

~~Выполнил: ученик 8 класса~~

~~Руководитель: учитель физики~~

~~2. Погрешности узкого сосуда. . . . . . . . . . . . . . . . . . . . . . . . .4-6~~

~~3. «Прилипание» к дну и стенкам . . . . . . . . . . . . . . . . . . . ….6-7~~

~~4. Закон Архимеда в невесомости . . . . .. . . . . . . . . . . . . . . . 7-8~~

~~5. Ускорение и сила Архимеда . . . . . . . . . . . . . . . . . . . . . . . 8-9~~

~~6. Выводы . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . .. . 9~~

~~7. Литература . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . .. . . 10~~

В школе изучается много различных законов. Большинство из них имеют те или иные границы применимости. Знания о границах применимости позволяют безошибочно применять законы в различных ситуациях. Проводя некоторые опыты и получая не совпадающие с теорией результаты, возникла идея о выяснении условий, при которых закон гидростатики не выполняется. Чтобы тщательно изучить этот вопрос, необходимо было найти и обработать большое количество информации, провести ряд опытов. Вся эта работа- внесение своего вклада в науку. Возможно, данный материал не имеет практической значимости, но работать над этим материалом было очень интересно.

2. Чтобы детально разобраться в вопросе о границах применимости закона Архимеда, нужно начать с рассмотрения необходимой, возможно знакомой всем, информации.

Закон Архимеда впервые был упомянут им в трактате «О плавающих телах». Архимед писал: » тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».

Этот закон, едва ли не первый физический закон, с которым мы знакомимся в школе. Он справедлив не только для жидкостей, но и для газов. Сила, выталкивающая погруженное тело, называется архимедовой, или гидростатической, подъемной силой. Появляется она потому, что верхняя и нижняя поверхности тела находятся на разной глубине и, следовательно, испытывают разные силы давления со стороны выше лежащих слоев газа или жидкости.

Воздух сжимаем, у поверхности Земли его плотность заметно выше, чем на высоте нескольких километров. Поэтому воздушный шар, увлекаемый вверх архимедовой силой, остановится, дойдя до некоторой высоты, на которой вес вытесненного воздуха станет равным весу шара. Вода практически несжимаема, поэтому в ней такой картины наблюдать нельзя: если тело начало тонуть, то оно опустится до самого дна.

Всё кажется простым и знакомым. Но всё ли так просто, как кажется? Чтобы ответить на этот вопрос, попробуем объяснить результаты одного эксперимента.

~~Эксперимент. Оборудование: широкий сосуд (таз), песок, два сосуда, вода.~~

~~Ход выполнения: 1 . Наполним широкий сосуд водой на ¾ объема.~~

Два других сосуда необходимо подобрать таких размеров, чтобы один входил в другой с небольшим зазором. Для наглядности эксперимента можно взять градуированную стеклянную банку и цилиндрическую мензурку, но можно использовать и два любых сосуда, для которых выполняются те же условия (небольшой зазор).

2 . В меньший сосуд (банку) насыплем такое количество песка, чтобы она держалась на плаву в широком сосуде с водой.

~~3 .Отметим на стенке мензурки глубину её погружения.~~

~~4 .Определим примерное значение веса банки с песком.~~

Если в эксперименте используется сосуд с делениями, то объём вытесненной воды можно примерно принять равным величине деления на сосуде, до которого произошло погружение. (В др.случае можно воспользоваться измерительным цилиндром и отливным сосудом для определения объёма вытесненной жидкости.)

Поскольку банка находится в состоянии равновесия, плавает, то, значит, ее вес скомпенсирован выталкивающей силой, равной весу вытесненной жидкости. По количеству вытесненной воды можно определить вес банки с песком. (Примерное значение.)

5 . Наполним цилиндрическую мензурку водой так, чтобы её вес был в 1,5-2 раза меньше веса банки с песком и опустим в неё банку с песком. Будет ли плавать эта банка с песком в сосуде (мензурке) немного большего диаметра, в который налито воды меньше, чем необходимо для плавания тела по закону Архимеда? (снимок I)

Естественно предположить, что выталкивающей силы уже не хватит на то, чтобы скомпенсировать вес банки и что банка с песком просто встанет на дно. Чтобы выяснить это, продолжим эксперимент.

7. Наблюдая за банкой убеждаемся в том, что банка, как и в опыте с широким сосудом плавает, погрузившись до того же, деления, что и при плавании в широком сосуде.

~~Это неожиданный результат. В чем же здесь дело? Почему она плавает?~~

Чтобы ответить на эти вопросы, нужно вспомнить другой закон гидростатики, открытый в XVII веке французским ученым Б. Паскалем и носящий его имя: «Давление, создаваемое внешними силами, передаетcя без изменения в каждую точку жидкости». В жидкости, находящейся под действием только одной силы тяжести, давление одинаково во всех точках любой горизонтальной плоскости. Эти плоскости называются поверхностями уровня или поверхностями равного давления. Пример такой плоскости — горизонтальная поверхность уровня в сообщающихся сосудах, например, в чайнике и его носке. Давление на любом уровне зависит только от высоты столба жидкости над ним и не зависит от ее массы. Поэтому общая сила F, которая давит на дно сосуда (она равна произведению давления Р на площадь дна S), может быть и больше и меньше веса воды, налитой в сосуд (см, рисунок), в зависимости от формы сосуда. Это на первый взгляд странное явление, открытое Б. Паскалем, получило название «гидростатический парадокс». Оно наводит на мысль, что в сосуде определённой формы можно получить огромные силы давления очень малым количеством жидкости. Сам Паскаль демонстрировал это с помощью бочки с водой и присоединённой к ней тонкой вертикальной трубки, длиной несколько метров. Когда в трубку влили пару кружек воды, наполнив ее доверху, бочка лопнула под действием силы давления F, равной весу столба воды высотой в несколько метров

(давление Р) и диаметром с бочку (площадь S)! Давление в жидкости передается во все стороны одинаково, поэтому струи воды из щелей хлынули во все стороны практически с равной силой,

Гидростатический парадокс приводит к разгадке «неправильного» поведения банки с песком в опыте с «узким» сосудом. Тонкий слой воды, оставшийся между стенками сосудов (банки с песком и мензурки), оказывает такое же давление на дно банки с песком, что и столб воды той же высоты в сосуде большого объема. Именно это давление и заставляет банку плавать.

Следовательно, чем уже зазор между стенками, тем меньшее количество воды вытеснит плавающее тело , тем сильнее нарушается закон Архимеда. Если бы не силы поверхностного натяжения, которые могут играть заметную роль при очень узком зазоре, любое тело можно было бы заставить плавать, в любом, сколь угодно малом количестве воды. Кажется непонятным, что о столь заметном нарушении закона Архимеда не упоминается ни в одном из многочисленных учебников и справочников по физике. Ведь это явление следовало бы, наверное, учитывать при гидростатическом взвешивании, когда определяют вес тела , погруженного в жидкость, при работе с ареометром, которым измеряют плотность жидкости и в других случаях.

Возникает вопрос о поправках к закону Архимеда, о границах его применимости. Но при более детальном рассмотрении этого вопроса становится ясно, что на самом деле эти поправки не нужны.

Если в опыте с «узким» сосудом мензурку наполнить водой до краев и опустить в него банку с песком, то собранной вылившейся воды будет столько, сколько и должно было быть вытеснено по закону Архимеда.

Учитывая это можно прийти к общепризнанному выводу о том, что закон Архимеда — частный случай закона Паскаля, справедливый только для больших объемов жидкости. Поэтому определение выталкивающей силы (равна весу вытесненной жидкости), которое дал Архимед, не подходит к случаю плавания тел в малых объёмах жидкости. Следовательно, в случае с малыми объёмами жидкости, применение закона Архимеда ограничено.

3 .Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем одной из сторон прижато ко дну или стенке сосуда.

При рассмотрении закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис.)

Это явление учитывается при подъёме затонувших кораблей. Прежде чем приступить к подъёму, затонувшее судно вначале «отрывают» от дна и только затем приступают непосредственно к подъёму.

4 . Тело, погруженное в жидкость, вытеснит часть этой жидкости. На нее, со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это — вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета, называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.

Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m(g + a). Это значит, что вес ящика равен Р = m(g + a), в то время как сила тяжести, действующая на ящик, равна mg. Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m(g — a).

Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями. Подтверждением этого служит отсутствие в невесомости явления естественной конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.

В земных условиях убедиться в том, что закон Архимеда в невесомости не действует, можно с помощью опыта с «картезианским водолазом». Нажмите на корпус бутылки так, чтобы водолаз опустился на дно. Затем «поместите его в невесомость»: подбросив (или уронив) бутылку, не изменяя её вертикального положения. Следите за поведением водолаза во время свободного полёта: всплывёт он или нет. В эти краткие мгновения на бутылку действует только сила тяжести (силой сопротивления воздуха можно пренебречь) и её содержимое находится в невесомости. Для получения более точных данных нужно повторить опыт несколько раз и можно самостоятельно сделать вывод о действии закона Архимеда в невесомости.

5 . Рассмотрим ситуацию, в которой сила Архимеда девствует на тело, движущееся с ускорением внутри жидкости. Будет ли в этом случае выполняться закон Архимеда? Представим себе легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= ρ Vg и сила натяжения нити T, а вверх — сила гидростатического давления F=F Арх = -ρVg, (*)

~~где ρ т — плотность тела, ρ — плотность жидкости. Условие равновесия тела~~

~~-ρVg +T+ ρ т Vg =0. (1)~~

Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вверх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения

~~F+ ρ т V g = ρV a. (2)~~

Предположив, что в этом случае можно использовать закон Архимеда, подставим — -ρVg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение

~~a = — g (ρ- ρ т )/ ρ т (3)~~

Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.

Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости)

В окружающем нас мире происходит огромное количество различных по своей природе явлений. Некоторые из них, даже при современном уровне развития науки, остаются загадками для человека. Много тайм хранит в себе бескрайняя вселенная и микромир. Но всё это многообразие явлений подчиняется вполне определённым законам, которые мы уже открыли и которые ещё предстоит открыть. Поэтому при изучении законов не может быть мелочей и выяснение границ применимости – тоже очень важно. Эти знания помогут понять, где и как можно применять тот или иной закон, расширят кругозор.

~~1. Применение закона Архимеда ограничено к случаю плавания тел в малых объёмах жидкости.~~

~~2. Закон Архимеда не распространяется на тела, находящиеся в состоянии невесомости.~~

~~3.При ускоренном движении тела, находящегося в жидкости или газе, расчёт силы Архимеда затруднён.~~

~~nsportal.ru~~