Глава VII
Математические основы

§7. Законы Кеплера

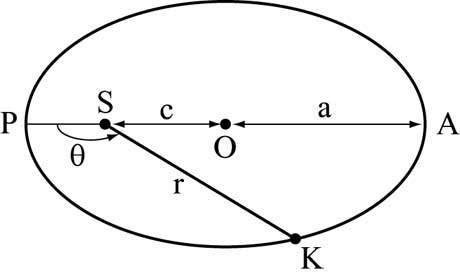
Первый закон . Планеты движутся по эллипсам, в общем фокусе которых находится Солнце.

Уравнение эллипса в полярной системе координат с полюсом в Солнце и с полярной осью, проходящей через перигелий, имеет вид:

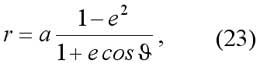
где e=c/a — эксцентриситет. Отсюда следуют выражения для минимального и максимального расстояния планеты от Солнца: q=a(1-e) и Q=a(1+e). Например, для орбиты Земли a=149,6×10 6 км, e=1/60, q=147,1×10 6 км и Q=152,1×10 6 км.

Второй закон (закон площадей): за одинаковые промежутки времени радиус-вектор планеты ометает равные площади. На рис.63 точки К 1 , К 2 , К 3 и К 4 — положения планеты в моменты t 1 , t 2 , t 3 и t 4 соответственно. Если t 2 -t 1 =t 4 -t 3 , то площади секторов К 1 SК 2 и К 3 SК 4 одинаковы. Из рис.63 видно, что дуга орбиты К 3 К 4 длиннее дуги К 1 К 2 . Следовательно, чем ближе планета к Солнцу, тем больше ее скорость .

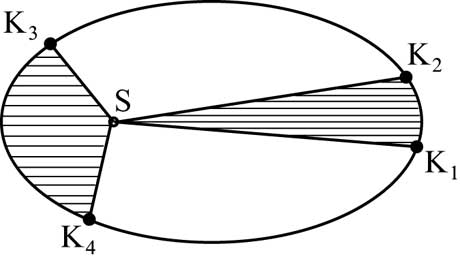
Второй закон можно записать в виде:

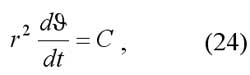
где 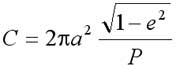и угол q выражен в радианах; Р — период обращения планеты вокруг Солнца.

Из второго закона Кеплера следует, например, что в перигелии скорость Земли в 1,0339 раз больше, чем в афелии (разность скоростей составляет примерно 1 км/с).

Третий закон: квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их орбит. Его можно записать так:

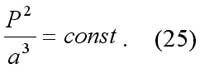
Если время выражать в периодах обращения Земли вокруг Солнца, а расстояния — в астрономических, единицах (1 а.е.= 149,6×10 6 ), то третий закон примет особенно простой вид: P=a 3/2

Ньютон обобщил (и уточнил) все эти законы на случай двух произвольных материальных точек с массами m 1 и m 2 , притягивающихся друг к другу по закону всемирного тяготения (других сил нет). Точки находятся по разные стороны от центра масс их системы, который делит отрезок, соединяющий точки, на части, длины которых обратно пропорциональны массам соответствующих точек. При этом каждая из них движется по эллипсу, в фокусе которого находится указанный центр масс, рис,64.

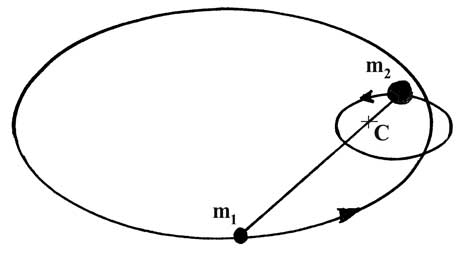
Однако при достаточно больших скоростях точек орбитами могут быть также парабола или гипербола.

Случаи, рассмотренные Кеплером соответствуют ситуации, когда начало системы отсчёта помещено в Солнце (например, в массу m 1 рис.64). Планета же (масса её — m 2 ) движется по эллипсу с фокусом в первой точке. Притяжения других планет не учитываются. Математическая запись уточнённого третьего закона Кеплера такова:

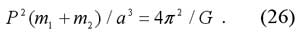
В таком виде закон применяют при определении масс двойных звёзд, а также масс планет, у которых имеется спутник. Пусть, например, P и a — период обращения и большая полуось относительной орбиты спутника данной планеты (или звезды). Тогда сумма масс планеты и спутника (или первой и второй звезды) может быть найдена по формуле:

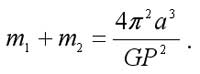
Как правило, массой спутника планеты можно пренебречь. Чтобы определить отношение масс звёзд, необходимо исследовать их орбиты относительно центра масс системы этих звёзд. Если a 1 и a 2 — большие полуоси соответствующих орбит, то справедливы равенства:

alexandr4784.narod.ru

КЕПЛЕРА ЗАКОНЫ

КЕПЛЕРА ЗАКОНЫ, принципы движения планет, сформулированные в начале 17 в. И.Кеплером (1571–1630) на основе многолетних наблюдений Т.Браге (1546–1601). Они используются в небесной механике и формулируются так:

1. Орбита любой планеты есть эллипс, в одном из фокусов которого находится Солнце.

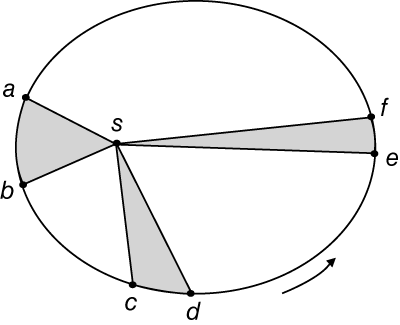
2. Планета движется так, что ее радиус-вектор за равные интервалы времени заметает равные площади. (Закон площадей.)

3. Квадраты периодов любых двух планет соотносятся как кубы их средних расстояний от Солнца. (Гармонический закон.)

Замечательно, что законы Кеплера, составляющие базис небесной механики, выведены из наблюдений Тихо, выполненных без телескопа.

Тихо поставил перед Кеплером задачу создания научной теории движения Марса. Следуя методике тех лет, Кеплер перепробовал множество комбинаций эпициклов и эксцентриков, но не смог найти подходящую для точного предвычисления наблюдаемого положения планеты. Наконец, он предположил, что орбита Марса эллиптическая, и увидел, что эта кривая хорошо описывает наблюдения, если Солнце поместить в один из фокусов эллипса. Затем Кеплер предположил (хотя и не мог точно доказать этого), что все планеты движутся по эллипсам, в фокусе которых находится Солнце. А орбиту Луны он описал эллипсом, в фокусе которого расположена Земля.

Действительно, орбиты всех больших планет – эллипсы, причем у Венеры орбита наиболее округлая (эксцентриситет е = 0,0068), а у Плутона наиболее вытянута (е = 0,2485). Орбиты малых планет – астероидов – тоже эллипсы; наиболее круглая орбита у астероида 1177 Гоннезия (е = 0,0063), а наиболее эксцентричная у 944 Идальго (е = 0,656).

Законы Кеплера полностью эмпирические, они выведены из наблюдений. Чтобы получить закон площадей, Кеплер трудился около восьми лет, проделав громадный объем вычислений. Чем ближе планета к Солнцу, тем быстрее она движется по орбите. Каждый год в начале января Земля, проходя через перигелий, движется быстрее; поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленно, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Третий, или гармонический, закон Кеплера связывает среднее расстояние планеты от Солнца (a) с ее орбитальным периодом (t):

где индексы 1 и 2 соответствуют любым двум планетам.

Пример: найти среднее расстояние от Солнца планеты Уран, имеющей период 84,015 лет. Из приведенной выше формулы, взяв период Земли за 1 год и ее расстояние от Солнца за 1 а.е.,

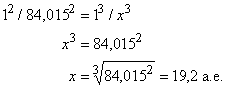
Ньютон (1643–1727) установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до нее, а не от других свойств, таких, как состав или температура. Он показал также, что закон Кеплера не совсем точен; что в действительности в него входит и масса планеты:

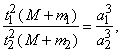
где M – масса Солнца, а m1 и m2 – массы планет. Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их расстояния и орбитальные периоды.

www.krugosvet.ru

3.1.3. Законы Кеплера

Три закона движения планет относительно Солнца были выведены эмпирически немецким астрономом Иоганном Кеплером в начале XVII века. Это стало возможным благодаря многолетним наблюдениям датского астронома Тихо Браге.

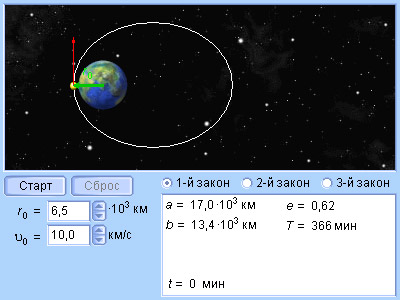
Первый закон Кеплера . Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

Второй закон Кеплера ( закон равных площадей ). Радиус-вектор планеты за равные промежутки времени описывает равновеликие площади. Другая формулировка этого закона: секториальная скорость планеты постоянна.

Третий закон Кеплера . Квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.

Современная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола.

В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам.

Скорость движения планеты в перигелии

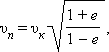
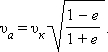
Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения. Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел.

В обобщенном виде этот закон обычно формулируется так: квадраты периодов T 1 и T 2 обращения двух тел вокруг Солнца, помноженные на сумму масс каждого тела (соответственно M 1 и M 2) и Солнца ( M ) , относятся как кубы больших полуосей a 1 и a 2 их орбит:

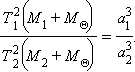
При этом взаимодействие между телами M 1 и M 2 не учитывается. Если пренебречь массами этих тел в сравнении с массой Солнца (т.е. M 1

college.ru


Добрый день! Недавно здесь проскакивал пост про уравнение Кеплера и я был слегка поражен тем, что ничего не написано про то, каким образом оно вообще выводится и откуда, как исторически, так и математически. Как известно, Кеплер вывел его из наблюдения движения планет, а Ландау и Лифшиц вывели движение планет из…

Никакая теоретическая механика невозможна без функции Лагранжа. Ее вывод я приводить не буду, скажу лишь, что вся соль в принципе наименьшего действия Гамильтона,

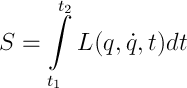
согласно которому, механическая система движется так, что вышеуказанный интеграл, который, кстати, называется действием, имеет наименьшее возможное значение. Возможно, «варьирование функционала» что-то вам говорит — если да, то уравнение Лагранжа (УЛ) (1), оно же уравнение Эйлера, для свободной частицы следует именно оттуда — это один из вариантов его вывода. Если нет, то все чуточку хуже, а именно: мы бы разобрали второй закон Ньютона, потратили около двух страниц на выкладки, ввели понятия обобщенных координат и сил и связей и в конечном итоге пришли бы к тому же варианту. Кстати, именно вторым способом функция Лагранжа (ФЛ) (2) вводится естественным образом, как разница кинетической и потенциальной энергий.

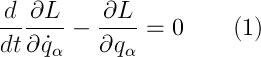
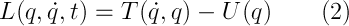
Касательно обозначений, q — обобщенная координата, точка — производная по времени. Важно! Согласно Лагранжева формализма, обобщенные координаты и скорости — независимые величины! В случае свободной частицы (или замкнутой системы, то есть системы, на которую не действуют внешние силы):

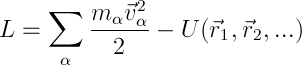
Индексы у обобщенных координат обозначают, что вообще это система дифференциальных уравнений для каждой координаты в отдельности.
Если коротко и в обратную сторону, заменив обобщенные координаты на радиус-векторы и скорости:

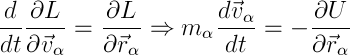
мы получаем уравнение Ньютона из уравнения Лагранжа (помня о том, что производная радиус-вектора по времени равна скорости).

Тут стоит еще добавить, что ФЛ аддитивна, что значит ФЛ системы есть сумма ФЛ ее частей:

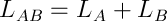
Отлично, у нас есть фундамент. Теперь, чтобы дойти до уравнения Кеплера, необходимо построить стены — обобщенные энергию, импульс и момент импульса. Здесь важно сделать маленькое утверждение, которое на самом деле очень большое и имеет название «Теорема Нётер»: наше пространство, по крайней в масштабах тех тел, которые мы описываем:

  • однородно,
  • изотропно,
  • обладает однородным временем.

    • Таким образом мы можем ввести три закона сохранения, три интеграла движения, то есть величины, сохраняющейся при движении, зависящей исключительно от начальных условий.

    Начнем с обобщенной энергии. Самое очевидное, что я могу сделать — вывести ее. Воспользуемся однородностью времени, а именно: ФЛ не зависит явно от времени, возьмем полную производную ФЛ и преобразуем, подставляя УЛ:

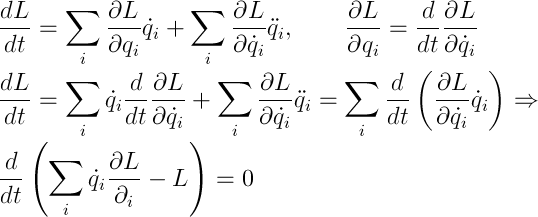
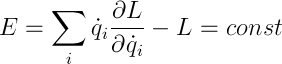
    Готово. Кстати, механические системы с сохраняющейся энергией называются консервативными.

    Сохранение обобщенного импульса следует из однородности пространства, а конкретно из свободы параллельного переноса системы в пространстве. Рассмотрим бесконечно малый перенос системы в пространстве на эпсилон, т.е. радиус-векторы частей системы изменятся как (1). Изменение ФЛ запишется как (2), что в силу произвольности эпсилон можно переписать так в виде равной нулю суммы частных производных. Дальше просто, (3) и мы видим, что суммарный импульс (4) не изменяется при движении.

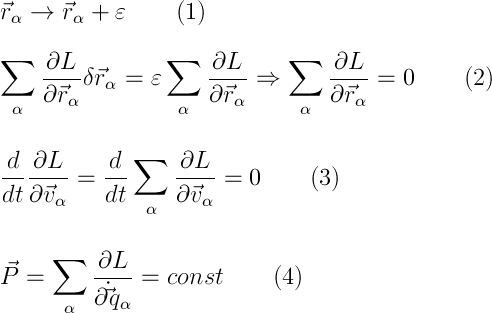
    Здесь же введем понятие центра инерции. Вообще механическая система интуитивно представима в виде некоторой точки, движущейся по прямой и остальных тел, которые каким-то образом движутся уже относительно этой точки. Так вот эта точка и есть центр инерции, то есть мы замкнутую механическую систему представим в виде некоторой точки с суммарной массой, а все остальное засунем во внутреннюю энергию системы.

    С моментом импульса, он же момент количества движения, все получается подобным образом, поэтому я просто выпишу результат:

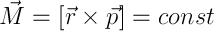
    Подытожим: у нас есть УЛ, ФЛ и три интеграла движения: энергия, импульс и момент количества движения.

    Можем переходить наконец к тому, из-за чего я отнимаю ваше время 🙂 То, из чего следует в частном случае уравнение Кеплера, называется «задача двух тел». Для начала упростим ее. Напишем ФЛ двух тел (1) и введем вектор их взаимного расстояния (2). Заодно поместим начало координат в центре инерции, что даст (3). Из второго и третьего уравнений найдем радиус-векторы обоих точек (4) и подставим в первое (5). Здесь введена приведенная масса (6).
    Таким образом задача двух тел сведена к задаче одного тела в некотором центральном поле.

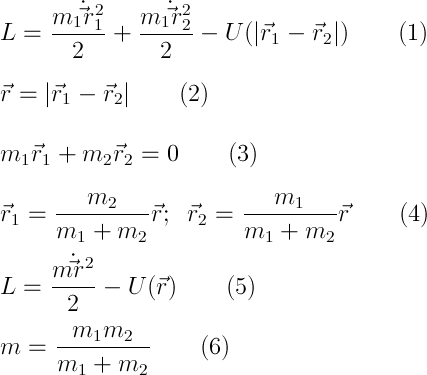
    Рассмотрим момент импульса в центральном поле M=[rp]. Отсюда М и r перпендикулярны, а из постоянства М (интеграл движения, помните?) видно, что радиус-вектор системы лежит всегда в одной плоскости — у нас плоское движение, а значит самое время ввести цилиндрическую систему координат с центром в силовом центре (простите за тавтологию) и осью z, перпендикулярной плоскости движения — по сути полярную. Перепишем ФЛ:

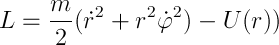
    и посмотрим на координату 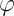— ее нет! Есть только ее производная по времени, что дает нам право обозвать ее циклической и сказать, что соответствующий ей обобщенный импульс сохраняется, а решение задачи упрощается. В данном случае он совпадает с моментом количества движения

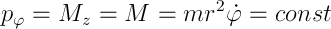
    Также в ФЛ не входит явно время, значит сохраняется заодно и энергия системы. Проведя серию выкладок

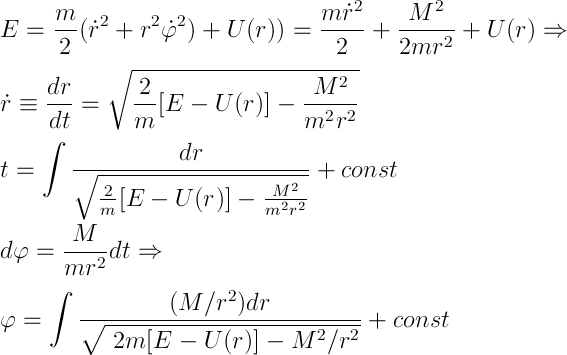
    получим решение задачи в квадратурах, то есть в интегралах. Заодно введем эффективную потенциальную энергию

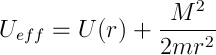
    А при чем тут уравнение Кеплера, слышно вопрос с задних рядов. Хорошо-хорошо, уговорили, я и сам как раз собирался…

    Давайте рассмотрим задачу о движении в центральном потенциальном поле

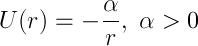
    Знак минус обозначает притяжение (а знак плюс означал бы отталкивание, что в данном случае нам не интересно — частица отразится и уйдет на бесконечность). Эта задача даже имеет собственное имя — да, задача Кеплера. Построим эффективную потенциальную энергию и ее график. Очевидно, что при стремлении r к нулю, она стремится к бесконечности, а при стремлении радиус-вектора к бесконечности, соответственно, к нулю.

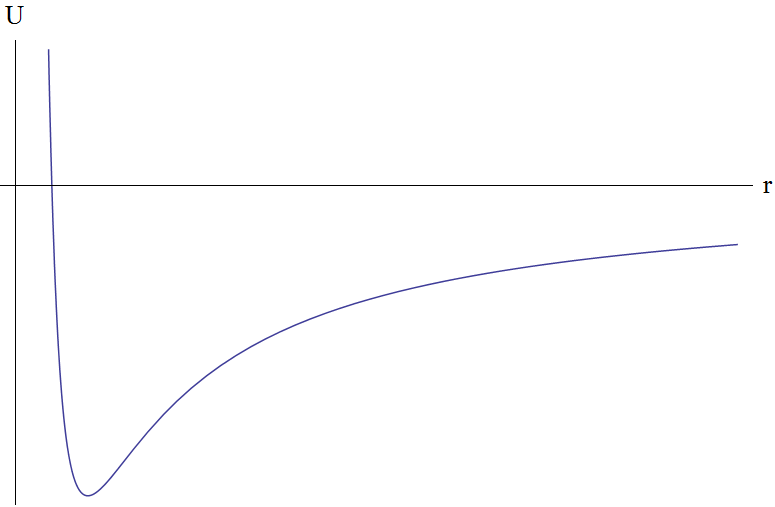
    Из графика очевидно, что при энергии Е > 0 движение будет инфинитным, то есть частица уйдет на бесконечность, а при E 0, e>1. Траектория опять инфинитна, но на этот раз это гипербола, с перигелием


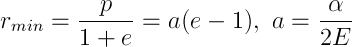
Пожалуй, это все, что я хотел бы рассказать про одну из фундаментальных задач механики. Задача Кеплера часто используется для проверки систем математического моделирования, как очень хорошо изученная и вместе с тем простая. Вместе с задачей о гармоническом осцилляторе это одна из двух задач о движении тела по замкнутой траектории, когда тело возвращается в исходную точку с той же самой скоростью. Задача Кеплера используется для построения новых методов классической механики, в частности Гамильтонова формализма, уравнения Гамильтона-Якоби и системы переменных «действие-угол».

m.habr.com

Правило кеплера

1.24. Законы Кеплера

В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.

Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.

Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.

С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (

140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.

Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном И. Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Т. Браге.

Первый закон Кеплера (1609 г.):

Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием , точка A , наиболее удаленная от Солнца – афелием . Расстояние между афелием и перигелием – большая ось эллипса.

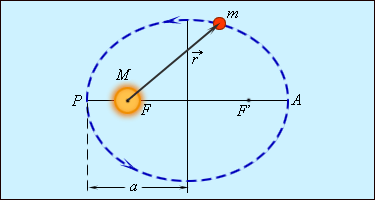
Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рис. 1.24.3 изображен вектор импульса тела 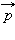и его составляющие 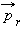и 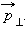Площадь, заметенная радиус-вектором за малое время Δ t , приближенно равна площади треугольника с основанием r Δθ и высотой r :

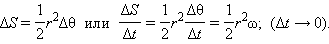
Здесь 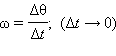– угловая скорость (см. §1.6).

Момент импульса L по абсолютной величине равен произведению модулей векторов 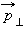и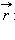

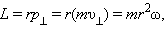так как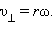

Из этих отношений следует:

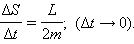
Поэтому, если по второму закону Кеплера 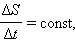то и момент импульса L при движении остается неизменным.

В частности, поскольку скорости планеты в перигелии 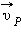и афелии 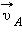направлены перпендикулярно радиус-векторам 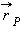и 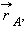из закона сохранения момента импульса следует:

Третий закон Кеплера (1619 г.):

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:

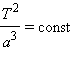или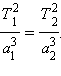

Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше 1 % .

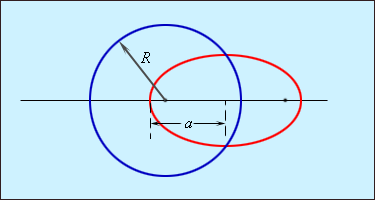
На рис. 1.24.4 изображены две орбиты, одна из которых – круговая с радиусом R , а другая – эллиптическая с большой полуосью a . Третий закон утверждает, что если R = a , то периоды обращения тел по этим орбитам одинаковы.

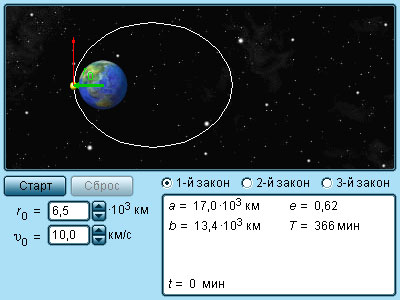
Несмотря на то, что законы Кеплера явились важнейшим этапом в понимании движения планет, они все же оставались только эмпирическими правилами, полученными из астрономических наблюдений. Законы Кеплера нуждались в теоретическом обосновании. Решающий шаг в этом направлении был сделан Исааком Ньютоном, открывшим в 1682 году закон всемирного тяготения :

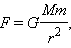
Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2

R 3 , где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:

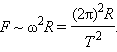
R 3 , то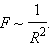

Свойство консервативности гравитационных сил (см. §1.10) позволяет ввести понятие потенциальной энергии . Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.

Потенциальная энергия тела массы m , находящегося на расстоянии r от неподвижного тела массы M , равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность.

Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5).

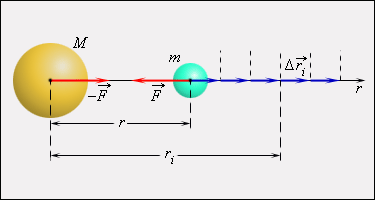
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам . Работа 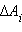гравитационной силы 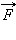на малом перемещении 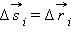есть:

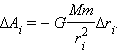
Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ Δ A i на малых перемещениях:

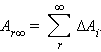
В пределе при Δ r i → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение

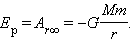
Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.

Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ , его полная механическая энергия равна

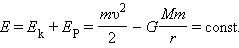
В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.

Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6).

При E = E 1 r max . В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).

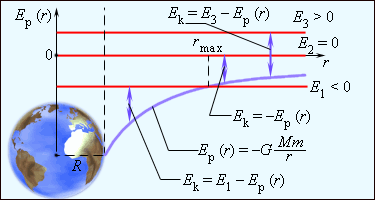
При E = E 2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории .

При E = E 3 > 0 движение происходит по гиперболической траектории . Тело удаляется на бесконечность, имея запас кинетической энергии.

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли.

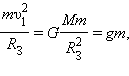отсюда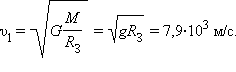

Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.

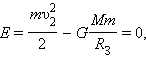отсюда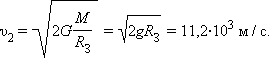

Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·10 3 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1 , но меньших υ2 = 11,2·10 3 м/с , орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.

physics.ru