Большая Энциклопедия Нефти и Газа

Основной закон — электромагнитная индукция

Основной закон электромагнитной индукции гласит, что индуцированный ток возникает в проводящем контуре при всяком изменении магнитного потока, пронизывающего площадь, охваченную этим контуром. Однако, производя совершенно одинаковое изменение магнитного потока в различных контурах, отличающихся только материалом, из которого сделаны эти контуры, мы обнаружим, что в них индуцируются токи различной величины. ГИзготовим, например, две катушки, совершенно одинаковые по величине, форме и числу витков, одну из медной проволоки, а другую из нихромовой проволоки того же сечения и длины, и поместим их в одно и то же магнитное поле, например, внутрь длинного соленоида, одинаково ориентировав катушки по отношению к направлению поля. [2]

Но, согласно основному закону электромагнитной индукции , ЭДС индукции в обмотке равна — S ( dB / dt) N, где В — индукция в магнетике, S — его сечение ( равное площади витка), N — полное число витков обмотки. [3]

Фигурирующий в основном законе электромагнитной индукции (25.2) магнитный поток Фш сквозь поверхность, натянутую на контур, может изменяться по ряду причин — благодаря изменению формы контура и его расположения в магнитном поле, а также вследствие переменности самого магнитного поля. S, натянутой на контур L, магнитная индукция В изменяется с течением времени. [4]

Покажите, что основной закон электромагнитной индукции является следствием закона сохранения энергии. [5]

Гельмгольц показал, что основной закон электромагнитной индукции (19.2) является следствием закона сохранения энергии. [6]

Полученный результат (19.8) по своей форме тождествен уравнению (19.2) основного закона электромагнитной индукции . Однако смысл правой части этого уравнения для контура и отрезка проводника различен. [7]

Формула (19.2), объединяющая законы Фарадея и Ленца, является математическим выражением основного закона электромагнитной индукции : электродвижущая сила электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, натянутую на контур. [8]

Формула (11.37), так же как и формулы (11.36) и (11.35), выражают собой основной закон электромагнитной индукции Фарадея Максвелла. [9]

Прежде всего отметим, что индуктированная во вторичном контуре эдс всегда отстает по фазе на 90 от создавшего ее первичного тока — это следует из основных законов электромагнитной индукции . Действительно, индуктированная эдс тем больше, чем больше скорость изменения тока. Но ток наиболее сильно изменяется при переходе через нулевое значение, поэтому в данный момент индуктированная эдс наибольшая. А когда ток достигает а мплитуд-ного значения, то скорость его изменения становится равной нулю и индуктированная эдс тоже уменьшается до нуля. По закону Ленца знак индуктированной эдс всегда должен быть таким, чтобы созданный ею во вторичном контуре ток своим магнитным полем противодействовал изменению первичного тока. Отсюда следует, что при возрастании-тока в первичном контуре эдс во вторичном контуре противоположна ему по знаку, а при убывании этого тока она совпадает с ним По знаку. Именно это и соответствует отставанию эдс во втором контуре на 90 от тока в первом контуре. [10]

Основной закон электромагнитной индукции гласит, что индукционный ток возникает в проводящем контуре при всяком изменении магнитного потока, пронизывающего поверхность, охваченную этим контуром. [12]

Основной закон электромагнитной индукции гласит, что индукционный ток возникает в проводящем контуре при всяком изменении магнитного потока, пронизывающего поверхность, охваченную этим контуром. [14]

Поясните рисунками и опишите эксперименты, в которых устанавливается зависимость направления индукционного тока от характера изменения магнитного потока. Как формулируют правило Ленца и правило правой руки. Что называют ЭДС индукции. Какая формула выражает основной закон электромагнитной индукции . [15]

www.ngpedia.ru

Как определить направление индукционного тока? Профессор Петербургского университета Э.Х.Ленц в 1833 г. установил, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Это – существенный физический факт, демонстрирующий стремление системы сопротивляться изменению состояния.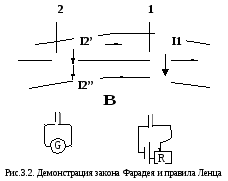

Вернемся к рис. 3.2. При увеличении тока I1, т.е. возрастании потока магнитной индукции Фm, направленного вправо, когдаdФm/dt>0, в контуре 2 возникает индукционный токI2 ’ , создающий собственный магнитный поток, направленный влево (данный поток стремится уменьшить Фm). ТокуI2 ’ соответствует εi ’ по правилу правого винта. Если ток в контуре 1 уменьшать, тоdФm/dt 0 и токI2 ” , собственный магнитный поток которого направлен так же, как и внешний поток Фm, потому что он стремится поддержать внешний поток постоянным, добавляя его.

Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.

Обобщением закона Фарадея и правила Ленца является закон Фарадея — Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

Это выражение представляет собой основной закон электромагнитной индукции.

При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.

Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εiв данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности:

Величину Ψ = ΣΦmназываютпотокосцеплениемили полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ =NΦm), то в этом случае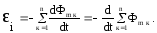

Немецкий физик Г.Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работаdA, совершаемая при перемещении контура за времяdt, будет составлять

где dФm– изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I 2 Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.

Разделив обе части равенства на Idt, получим

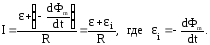
Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции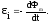

studfiles.net

17. Электромагнитная индукция. Закон электромагнитной индукции. Правило Ленца

Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина — магнитный поток. Магнитным потоком через замкнутый контур площадью (рис. 25) называют физическую величину, равную произведению модуля вектора магнитной индукции на площадь контура и на косинус угла между направлением вектора магнитной индукции и нормалью к площади контура: .

Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 В • с.

Основной закон электромагнитной индукции

4°. Знак минус в законе электромагнитной индукции соответствуетправилу Ленца: при всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым контуром, в последнем возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного потока, вызвавшего индукционный ток.

5°. Э. д. с. электромагнитной индукции возникает в отрезке проводника, пересекающем при своем движении линии индукции магнитного поля (III.10.1.3°). В случае, изображенном на рис. III.12.2, на электроны проводимости металла (III.7.3.1°) действует магнитное поле с силой Лоренца (III.11.1.1°):FЛ=–е[(v+v’)В], гдеv—скорость движения отрезка проводникаАСв магнитном поле, вектор индукцииBкоторого перпендикулярен плоскости, образованной отрезком проводника и вектором скорости его движения. Электроны упорядоченно движутся вдоль проводника со скоростьюv’. Это обусловлено тем, что сила Лоренца имеет ненулевую составляющую, касательную к проводнику и направленную отAкС. Движение электронов прекращается, когда возникшее в проводнике электростатическое поле, действующее на электроны с силойeE, скомпенсирует действие магнитного поля (силу Лоренца).

По закону Ома для разомкнутой цепи (при I= 0) (III.8.2.5°) равновесная разность потенциалов Δφ=φA–φCмежду точкамиАиС, которая установится приv’= 0, равна:

,

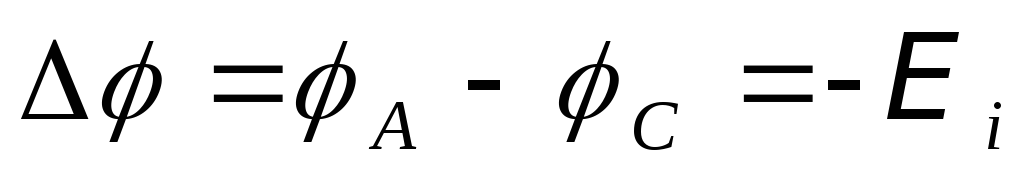где Ei– электродвижущая сила индукции, так как на участкеАСникаких источников электрической энергии нет.

Э. д. с. электромагнитной индукции на отрезке проводника длиной l, движущемся со скоростьюv,

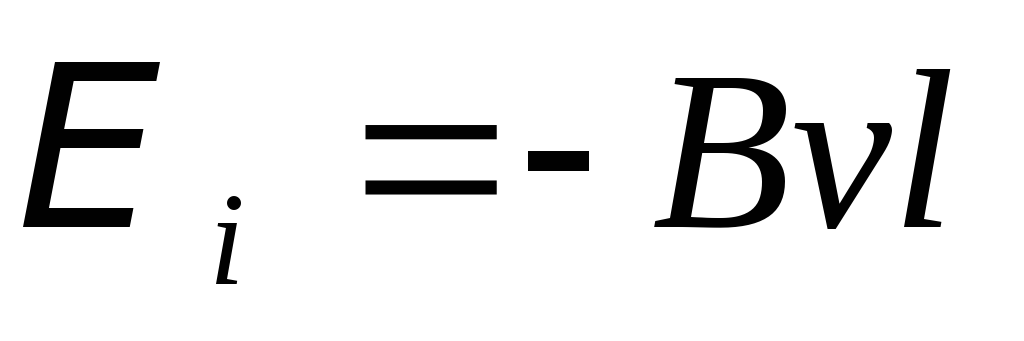
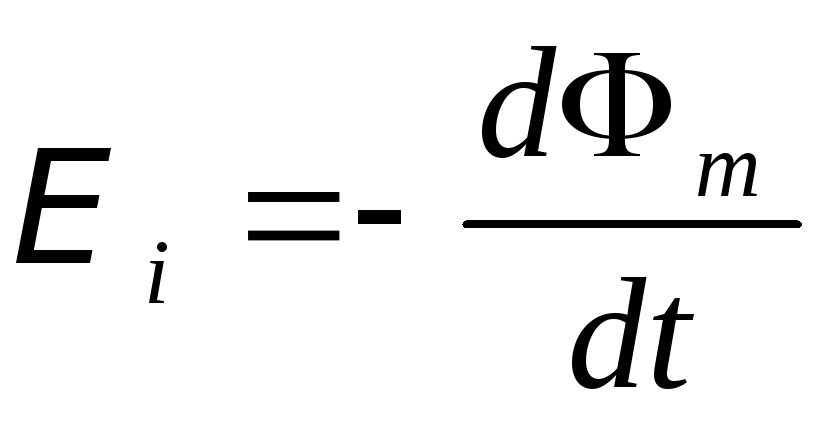(в СИ),

где 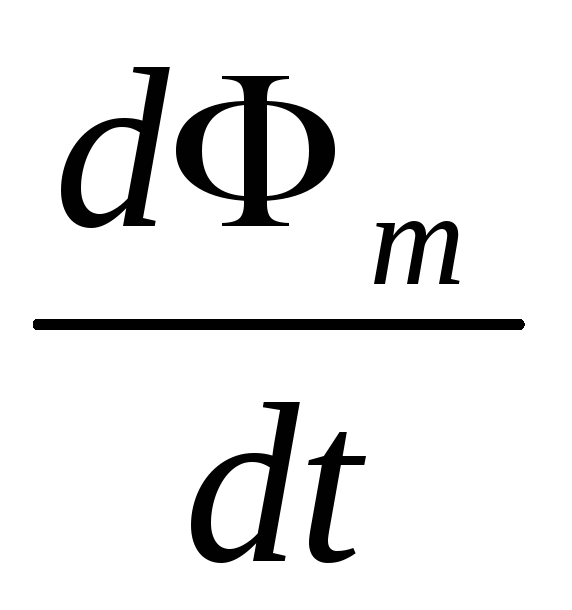– отношение магнитного потока сквозь поверхность, прочерчиваемую проводником при его движении за бесконечно малый промежуток времени, к величинеdtэтого промежутка, или, иначе, скорость пересечения проводником линий индукции магнитного поля (ср. (III.12.1.2°)).

6°. Явление электромагнитной индукции в неподвижных замкнутых проводниках, находящихся во внешнем переменном магнитном поле, не может быть объяснено с помощью силы Лоренца, так как магнитное поле не действует на неподвижные заряды (III.11.1.1º).

Явление электромагнитной индукции в неподвижных проводниках объясняется тем, что переменное магнитное поле вызывает появление вихревого электрического поля. Циркуляция напряженности этого поля вдоль замкнутого контура Lпроводника (III.3.1.4°) есть э. д. с. электромагнитной индукции:

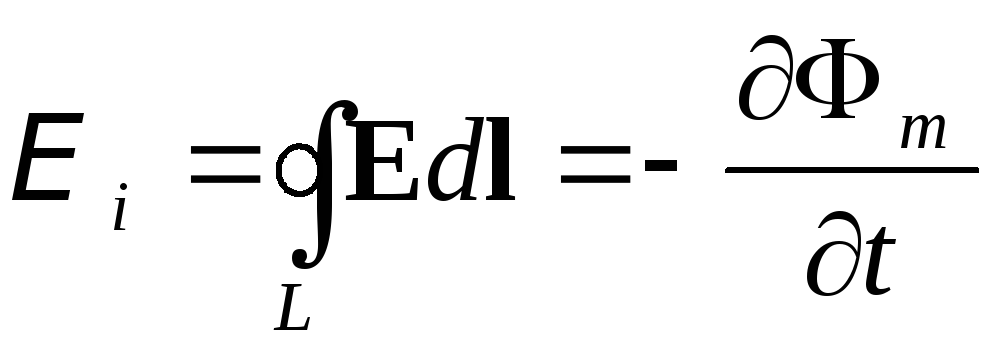(в СИ),

(в гауссовой системе),

где частная производная 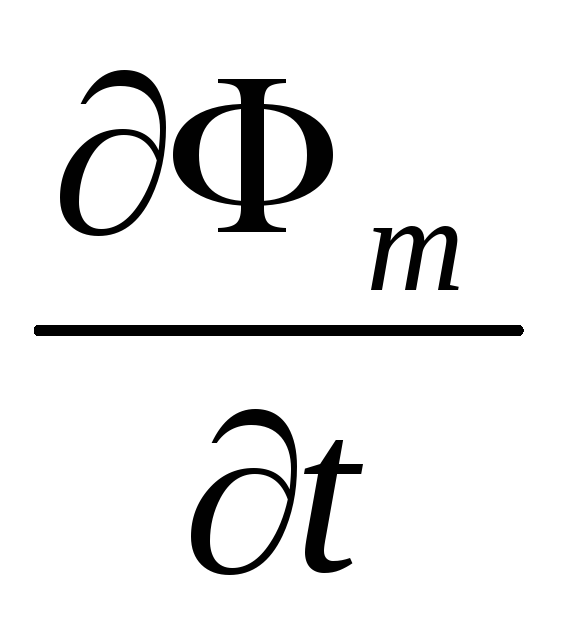учитывает зависимость потока магнитной индукции только от времени. О выборе направления нормалиnпри вычислении магнитного потока см. п. 2°.

7°. Величинаqэлектрического заряда, проходящего через поперечное сечение витка, в котором наводится индукционный ток:

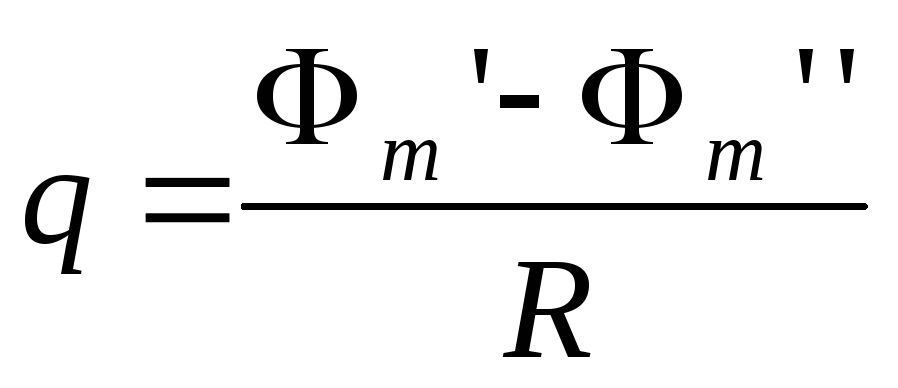(в СИ),

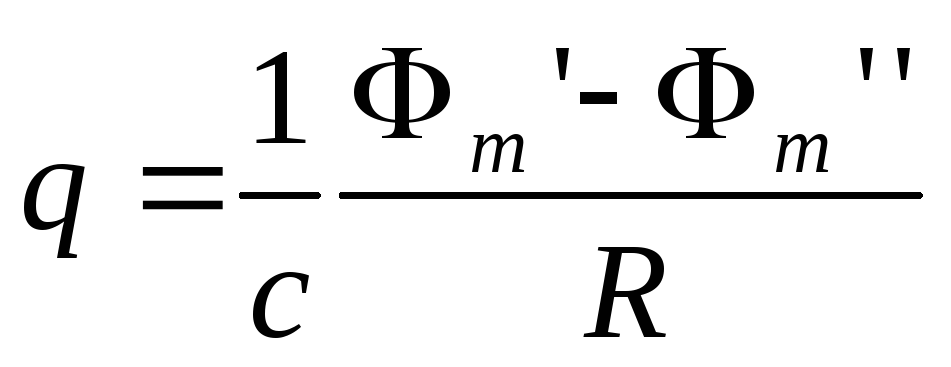(в гауссовой системе),

где Φm‘иΦm»– значения магнитного потока сквозь поверхность витка в его начальном и конечном положениях,R– электрическое сопротивление витка.

Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 г. Он опытным путем установил, что при изменении магнитного поля и и утри замкнутого проводящего контура в нем возникнет электрический ток, который называют индукционным током. Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 23). Если радом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 24). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное иоле всегда порождает переменное электрическое поле.

Опытным путем был установлен основной закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через контур: . Если рассматривать катушку, содержащую n витков, то формула основного закона электромагнитной индукции будет выглядеть так: .

Из основного закона следует смысл размерности: 1 вебер — это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нем ЭДС индукции 1 В.

Классической демонстрацией основного закона электромагнитной индукции является опыт Фарадея: чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.

Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур. В соответствии с правилом Ленца в законе электромагнитной идукции цолжен стоять знак минус:

Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло (рис. 26). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.

1. Нередки случаи, когда абитуриенты смешивают понятия магнитной индукции с понятием электромагнитной индукции. Это грубая ошибка: физическую велчину не отличают от явления.

Магнитная индукция — векторная фщическая величина, являющаяся силовой характеристикой магнитного поля.

Электромагнитная индукция — это явление возникновения электрического тока в проводящем контре при изменении магнитного потока через поверхность, ограниченную этим контуром.
[правил ]

www.fmclass.ru