I. Механика

Тестирование онлайн

— По какому закону вы собираетесь меня повесить?
— А мы вешаем всех по одному закону — закону Всемирного Тяготения.

Закон всемирного тяготения

Явление гравитации — это закон всемирного тяготения. Два тела действуют друг на друга с силой, которая обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их масс.

Математически мы можем выразить этот великий закон формулой

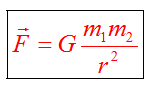
Тяготение действует на огромных расстояниях во Вселенной. Но Ньютон утверждал, что взаимно притягиваются все предметы. А правда ли, что любые два предмета притягивают друг друга? Только представьте, известно, что Земля притягивает вас, сидящих на стуле. Но задумывались ли о том, что компьютер и мышка притягивают друг друга? Или карандаш и ручка, лежащие на столе? В этом случае в формулу подставляем массу ручки, массу карандаша, делим на квадрат расстояния между ними, с учетом гравитационной постоянной, получаем силу их взаимного притяжения. Но, она выйдет на столько маленькой (из-за маленьких масс ручки и карандаша), что мы не ощущаем ее наличие. Другое дело, когда речь идет о Земле и стуле, или Солнце и Земле. Массы значительные, а значит действие силы мы уже можем оценить.

Вспомним об ускорении свободного падения. Это и есть действие закона притяжения. Под действием силы тело изменяет скорость тем медленнее, чем больше масса. В результате, все тела падают на Землю с одинаковым ускорением.

Чем вызвана эта невидимая уникальная сила? На сегодняшний день известно и доказано существование гравитационного поля. Узнать больше о природе гравитационного поля можно в дополнительном материале темы.

Задумайтесь, что такое тяготение? Откуда оно? Что оно собой представляет? Ведь не может быть так, что планета смотрит на Солнце, видит, насколько оно удалено, подсчитывает обратный квадрат расстояния в соответствии с этим законом?

Направление силы притяжения

Есть два тела, пусть тело А и В. Тело А притягивает тело В. Сила, с которой тело А воздействует, начинается на теле B и направлена в сторону тела А. То есть как бы «берет» тело B и тянет к себе. Тело В «проделывает» то же самое с телом А.

Каждое тело притягивается Землей. Земля «берет» тело и тянет к своему центру. Поэтому эта сила всегда будет направлена вертикально вниз, и приложена она с центра тяжести тела, называют ее силой тяжести.

Главное запомнить

1) Закон и формулу;
2) Направление силы тяжести

Практическое применение закона*

Некоторые методы геологической разведки, предсказание приливов и в последнее время расчет движения искусственных спутников и межпланетных станций. Заблаговременное вычисление положения планет.

Опыт Кавендиша*

Можем ли мы сами поставить такой опыт, а не гадать, притягиваются ли планеты, предметы?

Такой прямой опыт сделал Кавендиш (Генри Кавендиш (1731-1810) — английский физик и химик) при помощи прибора, который показан на рисунке. Идея состояла в том, чтобы подвесить на очень тонкой кварцевой нити стержень с двумя шарами и затем поднести к ним сбоку два больших свинцовых шара. Притяжение шаров слегка перекрутит нить — слегка, потому что силы притяжения между обычными предметами очень слабы. При помощи такого прибора Кавендишу удалось непосредственно измерить силу, расстояние и величину обеих масс и, таким образом, определить постоянную тяготения G.

Уникальное открытие постоянной тяготения G, которая характеризует гравитационное поле в пространстве, позволила определить массу Земли, Солнца и других небесных тел. Поэтому Кавендиш назвал свой опыт «взвешиванием Земли».

Связь с электричеством*

Интересно, что у различных законов физики есть некоторые общие черты. Обратимся к законам электричества (сила Кулона). Электрические силы также обратно пропорциональны квадрату расстояния, но уже между зарядами , и невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество как два разных проявления одной и той же сущности.

Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Как можно говорить, что одно действует сильнее другого? Ведь все зависит от того, какова масса и каков заряд. Рассуждая о том, насколько сильно действует тяготение, вы не вправе говорить: «Возьмем массу такой-то величины», потому что вы выбираете ее сами. Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.

Вопрос: каково отношение силы тяготения к электрической силе? Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число?

Люди ищут этот огромный коэффициент в других явлениях природы. Они перебирают всякие большие числа, а если вам нужно большое число, почему не взять, скажем, отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. И вот говорят: может быть, этот коэффициент и равен отношению диаметра протона к диаметру Вселенной? Это интересная мысль, но, поскольку Вселенная постепенно расширяется, должна меняться и постоянная тяготения. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.

Нюансы о действии притяжения*

Эйнштейну пришлось видоизменить законы тяготения в соответствии с принципами относительности. Первый из этих принципов гласит, что расстояние х нельзя преодолеть мгновенно, тогда как по теории Ньютона силы действуют мгновенно. Эйнштейну пришлось изменить законы Ньютона. Эти изменения, уточнения очень малы. Одно из них состоит вот в чем: поскольку свет имеет энергию, энергия эквивалентна массе, а все массы притягиваются, — свет тоже притягивается и, значит, проходя мимо Солнца, должен отклоняться. Так оно и происходит на самом деле. Сила тяготения тоже слегка изменена в теории Эйнштейна. Но этого очень незначительного изменения в законе тяготения как раз достаточно, чтобы объяснить некоторые кажущиеся неправильности в движении Меркурия.

Физические явления в микромире подчиняются иным законам, нежели явления в мире больших масштабов. Встает вопрос: как проявляется тяготение в мире малых масштабов? На него ответит квантовая теория гравитации. Но квантовой теории гравитации еще нет. Люди пока не очень преуспели в создании теории тяготения, полностью согласованной с квантовомеханическими принципами и с принципом неопределенности.

Дополнительные источники*

2) О различие эквивалентных формулировок закона гравитации. Лекция Ричарда Фейнмана «СВЯЗЬ МАТЕМАТИКИ С ФИЗИКОЙ»

fizmat.by

Объединение учителей Санкт-Петербурга

Основные ссылки

Закон всемирного тяготения. Сила тяжести.

Открыт Ньютоном в 1667 году на основе анализа движения планет (з-ны Кеплера) и, в частности, Луны. В этом же направлении работали Р.Гук (оспаривал приоритет) и Р.Боскович.

Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.

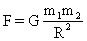
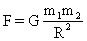
Закон справедлив для:

  • Однородных шаров.
  • Для материальных точек.
  • Для концентрических тел.

    • Гравитационное взаимодействие существенно при больших массах.

    Притяжение электрона к протону в атоме водорода » 2×10 -11 Н.

    Тяготение между Землей и Луной» 2×10 20 Н.

    Тяготение между Солнцем и Землей » 3,5×10 22 Н.

  • Закономерности движения планет и их спутников. Уточнены законы Кеплера.
  • Космонавтика. Расчет движения спутников.
  • Закон не объясняет причин тяготения, а только устанавливает количественные закономерности.
  • В случае взаимодействия трех и более тел задачу о движении тел нельзя решить в общем виде. Требуется учитывать «возмущения», вызванные другими телами (открытие Нептуна Адамсом и Леверье в 1846 г. и Плутона в 1930).
  • В случае тел произвольной формы требуется суммировать взаимодействия между малыми частями каждого тела.
  • Сила направлена вдоль прямой, соединяющей тела.
  • G — постоянная всемирного тяготения (гравитационная постоянная). Числовое значение зависит от выбора системы единиц.

    • В Международной системе единиц (СИ) G=6,67 . 10 -11 .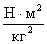

    G=6,67 . 10 -11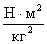

    Впервые прямые измерения гравитационной постоянной провел Г. Кавендиш с помощью крутильных весов в 1798 г.

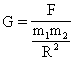
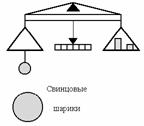
    Пусть m1=m2=1 кг, R=1 м, тогда: G=F (численно).

    Физический смысл гравитационной постоянной:

    гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга.

    То, что гравитационная постоянная G очень мала показывает, что интенсивность гравитационного взаимодействия мала.

    СИЛА ТЯЖЕСТИ

    Сила тяжести — это сила притяжения тел к Земле (к планете).

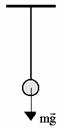
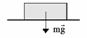
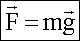
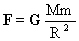    — из закона Всемирного тяготения. (где M — масса планеты, m — масса тела, R — расстояние до центра планеты).

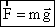    — сила тяжести из второго закона Ньютона (где m — масса тела, g — ускорение силы тяжести).

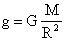    — ускорение силы тяжести не зависит от массы тела (опыты Галилея).

    g0=9,81 м/с 2 — на поверхности Земли

    Если обозначить R0 радиус планеты, а h — расстояние до тела от поверхности планеты, то: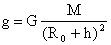

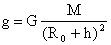
    Ускорение силы тяжести зависит:

  1. Массы планеты.
  2. Радиуса планеты.
  3. От высоты над поверхностью планеты.
  4. От географической широты (на полюсах — 9,83 м/с 2 . на экваторе — 9,79 м/с 2 .
  5. От залежей полезных ископаемых.

    www.eduspb.com

    Объяснение закона всемирного тяготения

    1.10. Закон всемирного тяготения. Движение тел под действием силы тяжести

    По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения .

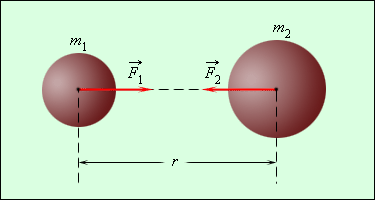
    Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). Понятие центра масс тела будет строго определено в § 1.23. У тела в виде однородного шара центр масс совпадает с центром шара.

    В последующие годы Ньютон пытался найти физическое объяснение законам движения планет (см. §1.24), открытых астрономом И. Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики . Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям ( прямая задача механики ), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.

    Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

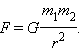
    Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной

    Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.

    Одним из проявлений силы всемирного тяготения является сила тяжести . Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, R З – ее радиус, m – масса данного тела, то сила тяжести равна

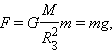
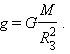
    Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с 2 . Зная ускорение свободного падения и радиус Земли ( R З = 6,38·10 6 м ), можно вычислить массу Земли М :

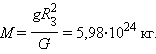
    При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н .

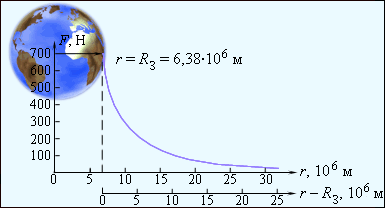
    Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии r Л = 3,84·10 6 м . Это расстояние приблизительно в 60 раз превышает радиус Земли R З . Следовательно, ускорение свободного падения a Л , обусловленное земным притяжением, на орбите Луны составляет

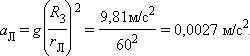
    С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением . Его можно рассчитать по кинематической формуле для центростремительного ускорения (см. §1.6):

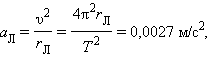
    Собственное гравитационное поле Луны определяет ускорение свободного падения g Л на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение g Л определится выражением:

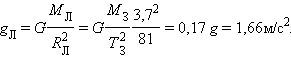
    В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м , то на Луне он мог бы подпрыгнуть на высоту более 6 м .

    Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км , и можно приближенно принять расстояние до центра Земли равным ее радиусу R З . Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g . Обозначим скорость спутника на околоземной орбите через υ1 . Эту скорость называют первой космической скоростью . Используя кинематическую формулу для центростремительного ускорения, получим:

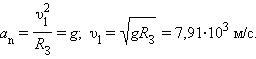
    Двигаясь с такой скоростью, спутник облетал бы Землю за время

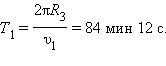
    На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.

    Движение спутника можно рассматривать как свободное падение , подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.

    Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия

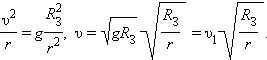
    Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.

    Период T обращения такого спутника равен

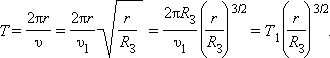
    Здесь T 1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 R З , период обращения спутника окажется равным 24 часам . Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 R З называется геостационарной .

    physics.ru

    Закон всемирного тяготения Ньютона

    На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения (см. Законы механики Ньютона), он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.

    Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории. Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение тел, падающих на поверхность Земли, они были уверены, что наблюдают явление чисто земной природы — существующее только недалеко от поверхности нашей планеты. Когда другие ученые, например Иоганн Кеплер (см. Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.

    Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.

    Результаты ньютоновских расчетов теперь называют законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:

    где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67 × 10 –11 .

    Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на все без исключения физические материальные тела во Вселенной. В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.

    Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на вас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и вы ее реально ощущаете как свой вес. Если вы что-нибудь уроните, оно под действием всё той же силы равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой g.

    Для Галилея g было просто экспериментально измеряемой константой. По Ньютону же ускорение свободного падения можно вычислить, подставив в формулу закона всемирного тяготения массу Земли M и радиус Земли D, помня при этом, что, согласно второму закону механики Ньютона, сила, действующая на тело, равняется его массе, умноженной на ускорение. Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.

    Наконец, закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.

    Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.

    Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.

    Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.

    Я допускаю, что кого-то из историков от моей версии хватит удар, но на самом деле меня этот вопрос мало беспокоит. Как бы то ни было, яблоко Ньютона остается красивой притчей и блестящей метафорой, описывающей непредсказуемость и таинство творческого познания природы человеком. А является ли этот рассказ исторически достоверным — это уже вопрос вторичный.

    elementy.ru

    Закон всемирного тяготения. Сила тяжести

    Два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

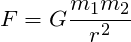
    Описание закона всемирного тяготения

    Коэффициент 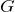— это гравитационная постоянная. В системе СИ гравитационная постоянная имеет значение: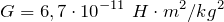

    Эта постоянная, как видно, очень мала, поэтому силы тяготения между телами, имеющими небольшие массы, тоже малы и практически не ощущаются. Однако движение космических тел полностью определяется гравитацией. Наличие всемирного тяготения или, другими словами, гравитационного взаимодействия объясняет, на чем «держатся» Земля и планеты, и почему они двигаются вокруг Солнца по определенным траекториям, а не улетают от него прочь. Закон всемирного тяготения позволяет определить многие характеристики небесных тел – массы планет, звезд, галактик и даже черных дыр. Этот закон позволяет с большой точностью рассчитать орбиты планет и создать математическую модель Вселенной.

    С помощью закона всемирного тяготения также можно рассчитать космические скорости. Например, минимальная скорость, при которой тело, движущееся горизонтально над поверхностью Земли, не упадёт на неё, а будет двигаться по круговой орбите – 7,9 км/с (первая космическая скорость). Для того, чтобы покинуть Землю, т.е. преодолеть ее гравитационное притяжение, тело должно иметь скорость 11,2 км/с, (вторая космическая скорость).

    Гравитация является одним из самых удивительных феноменов природы. В отсутствии сил гравитации существование Вселенной было бы невозможно, Вселенная не могла бы даже возникнуть. Гравитация ответственна за многие процессы во Вселенной – ее рождение, существование порядка вместо хаоса. Природа гравитации до сих пор до конца неразгаданна. До настоящего времени никто не смог разработать достойный механизм и модель гравитационного взаимодействия.

    Сила тяжести

    Частным случаем проявления гравитационных сил является сила тяжести.

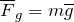
    Сила тяжести всегда направлена вертикально вниз (по направлению к центру Земли).

    Если на тело действует сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости.

    С действием силы тяжести мы сталкиваемся каждый день. Камень, брошенный в горизонтальном направлении, через некоторое время оказывается на земле. Книга, выпущенная из рук, падает вниз. Подпрыгнув, человек не улетает в открытый космос, а опускается вниз, на землю.

    Рассматривая свободное падение тела вблизи поверхности Земли как результат гравитационного взаимодействия этого тела с Землей, можно записать:

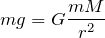
    откуда ускорение свободного падения:

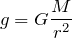
    Ускорение свободного падения не зависит от массы тела, а зависит от высоты тела над Землей. Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов, расположены немного ближе к центру Земли. 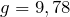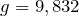В связи с этим ускорение свободного падения зависит от широты местности: на полюсе оно немного больше, чем на экваторе и других широтах (на экваторе м/с , на Северном полюсе экваторе м/с .

    Эта же формула позволяет найти ускорение свободного падения на поверхности любой планеты массой 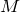и радиусом .

    Примеры решения задач

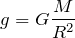
    откуда масса Земли:

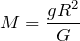
    В системе Си радиус Земли 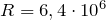м.

    Подставив в формулу численные значения физических величин, оценим массу Земли:

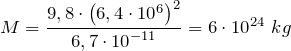
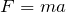
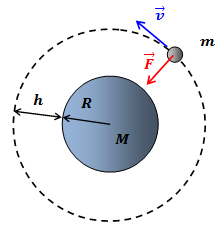
    Со стороны земли на спутник действует сила гравитационного притяжения, которая по закону всемирного тяготения равна:

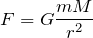
    где 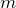и 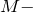массы спутника и Земли соответственно.

    Так как спутник находится на некоторой высоте 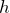над поверхностью Земли, расстояние от него до центра Земли: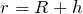

    где 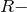радиус Земли.

    Таким образом, сила гравитационного притяжения в данном случае:

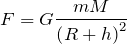
    Подставив значение гравитационной силы в формулу для второго закона Ньютона и учитывая, что ускорение спутника – это центростремительное ускорение (спутник движется по круговой орбите), получим:

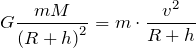
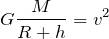
    откуда скорость спутника:

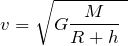
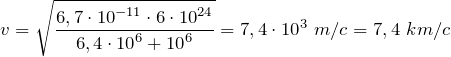
    Время, за которое спутник совершит один полный оборот вокруг Земли, — это период его обращения по круговой орбите, который равен:

    ru.solverbook.com