Физический смысл производной. Задачи!

Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость. Задачи очень простые, решаются они в одно действие. Итак:

Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.

Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.

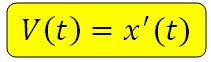
Аналогично, ускорение – это производная скорости по времени:

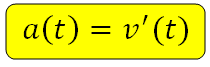
Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).

Кроме того, необходимо знать таблицу производных (знать её нужно также, как таблицу умножения) и правила дифференцирования. Если конкретно, то для решения оговоренных задач необходимо знание первых шести производных (см. таблицу):

x (t) = t 2 – 7t – 20

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.

Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)

Найдем закон изменения скорости: v (t) = x′(t) = 2t – 7 м/с.

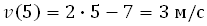
Материальная точка движется прямолинейно по закону x (t) = 6t 2 – 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c.

Материальная точка движется прямолинейно по закону x (t) = 0,5t 3 – 3t 2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.

x (t) = –t 4 + 6t 3 + 5t + 23

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.

Материальная точка движется прямолинейно по закону

x (t) = (1/6) t 2 + 5t + 28

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?

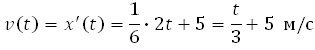
Для того, чтобы найти, в какой момент времени t скорость была равна 3 м/с, необходимо решить уравнение:

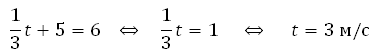
Материальная точка движется прямолинейно по закону x (t) = t 2 – 13t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?

Материальная точка движется прямолинейно по закону

x (t) = (1/3) t 3 – 3t 2 – 5t + 3

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Отмечу, что ориентироваться только на такой тип задач на ЕГЭ не стоит. Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.

Подсказка: в этом случае необходимо найти интеграл от функции скорости (это так же задачи в одно действие). Если потребуется найти пройденное расстояние за определённый момент времени, то необходимо подставить время в полученное уравнение и вычислить расстояние. Впрочем, мы такие задачи тоже будем разбирать, не пропустите! Успехов вам!

matematikalegko.ru

Материальная точка движется согласно закону s t

26 июняНовые варианты прошедших ЕГЭ по математике: здесь.

5 июня Наши мобильные приложения могут работать оффлайн.
Андроид iOS

− Examer из Таганрога;
− Учитель Думбадзе В. А.
из школы 162 Кировского района Петербурга.

Наша группа ВКонтакте
Мобильные приложения:

Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.

Найдем закон изменения скорости:

При t = 9 c имеем:

м/с.

Почему мы не учитываем число 17 из первоначального уравнения?

найдите производную исходной функции.

в производной нет числа 17

Зачем находить производную?

Скорость — это производная координаты по времени.

В задаче просят найти скорость

Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.

м/с.

м/с.

(6)=3/2*36-6*6+2=54-38=16,, а не 20

вспомните про порядок действий

А с каких пор сложение предпочтительнее вычитания ?

Умножение приоритетней сложения и вычитания. Вспомните детский школьный пример: 2 + 2 · 2. Напомню, что здесь получается не 8, как считают некоторые, а 6.

Вы, не поняли ответа гостя.

1,5*36 — 6*6 + 2 = 54 — 36 + 2 = 18 + 2 = 20.

Так-что всё верно, посчитайте сами.

2) умножение/деление (зависит от порядка в уравнении, что первое стоит — то и решается первым делом);

3) сложение/вычитание (аналогично зависит от порядка в примере).

Умножение = делению, сложение = вычитанию =>

Не 54 — (36+2), а 54-36+2 = 54+2-36 = 20

Во-первых, для вас — Сергей Батькович. Во-вторых, вы сами поняли, что и кому сказать хотели? Я вас не понял.

Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени с.

Найдем закон изменения скорости: м/с. При имеем:

м/с.

ege.sdamgia.ru

Урок по теме: «Правила дифференцирования», 11-й класс

Разделы: Математика

Тип урока: обобщение и систематизация знаний.

Цели урока:

  • образовательные:
    • обобщить, систематизировать материал темы по нахождению производной;
    • закрепить правила дифференцирования;
    • раскрыть для учащихся политехническое, прикладное значение темы;
    • развивающие:
      • осуществить контроль усвоения знаний и умений;
      • развить и совершенствовать умения применять знания в измененной ситуации;
      • развить культуру речи и умение делать выводы и обобщать;
    • воспитательные:
      • развить познавательный процесс;
      • воспитать у учащихся аккуратность при оформлении, целеустремленность.

      • Оборудование:

      • кодоскоп, экран;
      • карточки;
      • компьютеры;
      • таблица;
      • дифференцированные задания в виде мультимедиа презентации.

        • I. Проверка домашнего задания.

        1. Заслушать сообщения учащихся по примерам применения производных.

        2. Рассмотреть примеры применения производной в физике, химии, технике и других отраслях, предложенные учащимися.

        II. Актуализация знаний.

        Учитель:

    1. Дать определение производной функции.
    2. Какая операция называется дифференцированием?
    3. Какие правила дифференцирования используются при вычислении производной? (К доске приглашаются желающие учащиеся).
      • производная суммы;
      • производная произведения;
      • производная, содержащая постоянный множитель;
      • производная частного;
      • производная сложной функции;
      • Приведите примеры прикладных задач, приводящих к понятию производной.

    Ряд частных задач из различных областей наук.

    Задача № 1. Тело движется по прямой согласно закону х(t). Запишите формулу для нахождения скорости и ускорения тела в момент времени t.

    Задача № 2. Радиус круга R изменяется по закону R = 4 + 2t 2 . Определите, с какой скоростью изменится его площадь в момент t = 2 с. Радиус круга измеряется в сантиметрах. Ответ: 603 см 2 /с.

    Задача № 3. Материальная точка массой 5 кг движется прямолинейно по закону

    S(t) = 2t + 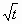, где S — путь в метрах, t – время в секундах. Найдите силу, действующую на точку в момент t = 4 с.

    Ответ: 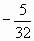Н.

    Задача № 4. Маховик, задерживаемый тормозом, поворачивается за t с на угол 3t — 0,1t 2 (рад). Найдите:

    а) угловую скорость вращения маховика в момент t = 7с;
    б) в какой момент времени маховик остановится.

    Ответ: а) 2,86 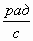; б) 150 с.

    Примерами применения производной также могут служить задачи на нахождение: удельной теплоемкости вещества данного тела, линейной плотности и кинетической энергии тела и т.д.

    III. Выполнение дифференцированных заданий.

    Желающие выполнять задания уровня “А”, садятся за компьютер и выполняют тест с программированным ответом. (Приложение.)

    1. Найдите значение производной функции 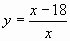в точке х0 = 3.

    2. Найдите значение производной функции у = хе х в точке х0 = 1.

    1) 2е;
    2) е;
    3) 1 + е;
    4) 2 + е.

    3. Решите уравнение f / (x) = 0 , если f (x) = (3x 2 + 1)(3x 2 – 1).

    1) ;
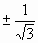    2) 2;
    3) ;
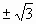    4) 0.

    4. Вычислите f / (1), если f (x) = (x 2 + 1)(x 3 – x).

    5. Найдите значение производной функции f(t) = (t4 – 3)(t2 + 2) в точке t0 = 1.

    6. Точка движется прямолинейно по закону: S(t) = t 3 – 3t 2 . Выбери формулу, которая задаёт скорость движения этой точки в момент времени t.

    1) t 2 – 2t;
    2) 3t 2 – 3t;
    3) 3t 2 – 6t;
    4) t 3 + 6t.

    xn--i1abbnckbmcl9fb.xn--p1ai