Справочник химика 21

Химия и химическая технология

Значащие цифры и правила округления

Значащие цифры и правила округления [c.55]

При оформлении окончательного резу.чьтата придерживаются следующего правила погрешность должна иметь одну-две значащие цифры, а число, выражающее среднее значение результата (измерения), должно оканчиваться разрядом, которым начинается погрещность, т. е. значения среднего результата и границ доверительного интервала должны быть выражены числами с одинаковым числом знаков после запятой их положено округлять в одинаковой степени. Правило округления чисел см. п. 2.7. [c.69]

Выражение получено при условии Пф = min = /г с учетом известного соотношения 5 ( ) = 5 (г/)/V — Множитель 4, / обычно не превышает 4—5. Поэтому погрешность в оценке предела обнаружения не менее 20 %. Отсюда вытекает, что значение предела обнаружения следует приводить с точностью до одной, максимум двух значащих цифр. При этом можно придерживаться следующего правила если первая значащая цифра не превосходит 3, допустимо указание цифр следующего десятичного раздела с округлением их до О или 5. Если первая значащая цифра больше 3, результат следует округлить до ближайшего целого числа и представить одной значащей цифрой с указанием десятичного разряда. [c.115]

Очень важным является правило округления в химических задачах. При округлении необходимо оставлять не менее трех значащих цифр. Чтобы пояснить, что такое значащая цифра, рассмотрим простой пример. Найдем количество вещества в 1,1 г нитрата цинка 7п(МОз)2 [c.455]

При расчетах окончательный результат обычно округляют. Округление следует проводить с соблюдением определенных правил, так как излишнее округление может ухудшить результаты анализа, а вычисления с неоправданно большим числом десятичных знаков без округления, требуют больших, но напрасных затрат труда, поскольку не улучшают реальной точности результата. Указание пяти-шести значащих цифр в результатах анализа обычно свидетельствует о некритическом отношении к погрешности числа. Необходимо напомнить, что нули, предшествующие первой цифре, отличной от нуля, значащими не являются. [c.132]

Большие трудности бывают обусловлены причинами, совершенно неожиданными для неопытного исследователя. Речь идет об ошибке, связанной с округлением величин. Для большинства нестатистических задач, проводя расчеты, можно брать величины, содержащие на одну или две значащие цифры больше, чем мы хотим получить в окончательном ответе. Однако в статистических расчетах этого, как правило, бывает недостаточно, потому что на том или ином их этапе непременно приходится определять разность двух близких величин, что всегда ведет к потере нескольких значащих цифр. Рассмотрим, например, разность 1,38204—1,38195 = 0,00009. Каждое из исходных чисел содержит шесть значащих цифр, а в разности мы имеем только одну. Полезно проделать расчет Км при помощи уравнения (10.29) для серии данных, приведенных в табл. 10.1. Так как численные значе- [c.256]

При округлении уменьшают число значащих цифр. Это всегда связано с введением некоторой погрешности от округления. Округление с поправкой предусматривает отбрасывание последней цифры, если она is 4, и увеличение на одну единицу предпоследней цифры, если последняя цифра >5. При округлении чисел с последней цифрой 5 выгоднее применять правило четной цифры, ибо результат округления всегда четный. Округление в этом случае всегда сводится к отбрасыванию единственной цифры 5, если предпоследняя цифра четная, и увеличение ее на единицу, если она нечетная. В результате округления вносится погрешность не более половины единицы последнего разряда. Например, округление чисел 217,5 и 218,5 дает цифру 218. Погрешность в обоих случаях равна половине цифры последнего разряда. [c.177]

Десятичными знаками называются все цифры числа, стоящие правее запятой, отделяющей его дробную часть. Значащими цифрами называются все цифры числа, кроме нулей, стоящих слева, и нулей, стоящих справа и заменяющих неизвестные или отброшенные при округлении цифры. Нули в середине числа всегда являются значащими цифрами. [c.17]

Если решить эту систему на ЭВМ, которая выполняет арифметические операции с точностью до 8 значащих цифр, и подставить в приведенную выше систему уравнений w = 1Е — 10, то в результате получится X = 1, у = 1. Этот результат не вызывает никаких возражений. Если же уравнения поменять местами, то по программе Г—Ж получится х = О, > = 1. Ясно, что этот результат ошибочный. Если в исходной системе уравнения поменять местами и разделить оба уравнения на w, то при решении полученной системы по программе Г—Ж получится х = 4,671875, = 1. Таким образом, операции, которые не должны были бы отражаться на решении системы уравнений, приводят к различным и, следовательно, ошибочным результатам. Появление ложных корней связано с тем, что ЭВМ производит арифметические действия с конечной точностью и в процессе вычисления накапливаются ошибки округления. Системы уравнений, которые ведут себя так же, как рассмотренная в этом примере, назьшают плохо обусловленными. Для систем уравнений с числом неизвестных больше двух, как правило, невозможно сразу установить, является ли эта система плохо обусловленной. Поэтому надо обязательно проверять, удовлетворяют ли в действительности найденные значения неизвестных исходной системе уравнений. [c.185]

В этом случае число 24 имеет две значащие цифры и в соответствии с этим округлен результат. К сожалению, данное правило не всегда применимо. Предположим, что погрешность числа 24 может быть малой, например 0,5, или большой, например 5. Погрешность частного для этих двух пределов определяется так [c.95]

Например, в результате измерения объема с помощью бюретки было получено 25,3 мл. Необходимо этот объем разделить на два. В результате деления получается 12,65 мл. Бюретка измеряет объем с точностью до 0,1 мл, значит второй знак не достоверен. Результат деления необходимо округлить до десятых долей 12,7 мл. Правило округления состоит в следующем если первая из отбрасываемых цифр 5 или более 5, то последнюю из оставляемых цифр надо увеличить на единицу. Когда первая из отбрасываемых цифр меньше 5, то увеличения не делают. Если исходные данные имеют различную величину относительных ошибок, то ошибка конечного результата вычислений определяется ошибкой наименее точного из исходных данных. Окончательный результат вычислений следует давать с тем числом значащих цифр, которое содержит его ошибка. [c.5]

В заключение отметим, что константы равновесия, сложных процессов и реакций, которые требуют для своего определения данных о равновесных концентрациях ряда компонентов, всегда вычисляются с существенно большими ошибками, чем сами концентрации. Поэтому лишены разумных оснований попытки определения констант с точностью до процентов. Необходимо ясно сознавать, что меры точности в определении аналитических концентраций и констант многокомпонентных реакций существенно различны. Константы, приводимые с тремя значащими цифрами, например 3,62-или 1,44-10 , как правило, претендуют на неоправданно завышенную точность определения. При оценке констант в лучших случаях погрешности достигают десятков, в ху1д-ших — сотен процентов. Поэтому значения констант следует приводить с заведомым округлением до одной, двух значащих цифр или, используя логарифмическую шкалу рК, lgP (отрицательный логарифм константы диссоциации, логарифм константы образр-вания комплекса), округлять до 0,05—0,1 единиц p (lgP). [c.131]

Смотреть страницы где упоминается термин Значащие цифры и правила округления: [c.28] [c.191] [c.8] [c.62] Смотреть главы в:

chem21.info

Правило округления чисел

В приближенных вычислениях зачастую приходится округлять некоторые числа, как приближенные, так и точные, то есть убирать одну или несколько конечных цифр. Для того чтобы обеспечить наибольшую близость отдельного округленного числа к округляемому числу, следует соблюдать некоторые правила.

Если первая из отделяемых цифр больше, чем число 5 , то последняя из оставляемых цифр усиливается, иначе говоря, увеличивается на единицу. Усиление так же предполагается и тогда, когда первая из убираемых цифр равна 5 , а за ней имеется одна или некоторое количество значащих цифр.

Число 25,863 округлённо записывается как – 25,9 . В данном случае цифра 8 будет усилена до 9 , так как первая отсекаемая цифра 6 , больше чем 5 .

Число 45,254 округлённо записывается как – 45,3 . Здесь цифра 2 будет усилена до 3 , так как первая отсекаемая цифра равна 5 , а за ней следует значащая цифра 1 .

В случае если первая из отсекаемых цифр меньше чем 5 , то усиления не производится.

Число 46,48 округлённо записывается как – 46 . Число 46 наиболее близко к округляемому числу, чем 47 .

Если отсекается цифра 5 , а за ней не имеется значащих цифр, то округление выполняется на ближайшее четное число, другими словами, последняя оставляемая цифра остаётся неизменной, если она четная, и усиливается в случае, если она нечетная.

Число 0,0465 округлённо записывается как – 0,046 . В данном случае усиления не делается, так как последняя оставляемая цифра 6 является чётной.

Число 0,935 округлённо записывается как – 0,94 . Последняя оставляемая цифра 3 усиливается, так как она является нечётной.

simple-math.ru

Рефераты и конспекты лекций по географии, физике, химии, истории, биологии. Универсальная подготовка к ЕГЭ, ГИА, ЗНО и ДПА!

Физика — рефераты, конспекты, шпаргалки, лекции, семинары

Правила округления значений погрешностей и результатов измерения

Погрешности измерений показывают также, какие цифры в полученном результате измерения сомнительны, поэтому нет смысла в записи погрешности с большим числом знаков.

По обычаю ограничиваются одной значащей цифрой и только при особо точных измерениях погрешность записывается двумя или тремя цифрами.

Используют 3 правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:

1. Погрешность результата измерения показывается двумя значащими цифрами, если первая из них 1 или 2, и одной — если первая цифра 3 и более.

2. Результат измерения округляется до того же десятичного разряда, которым заканчивается округления значение абсолютной погрешности.

3. Округление производится только в конечной ответы, а все предварительные расчеты проводят с одним — двумя лишними знаками.

В соответствии с правилом 1 установлены и нормированные значения погрешностей 3В: в числах 1,5% или 2,5% показываются два знака, но в числах 0,5%, 4%, 6%; показывается только один знак.

При округлении результатов измерения используют еще такие правила:

1) лишние цифры в целых чисел заменяют нулями, а в дробных десятичных отвергают; н., 732 «700.

2) если первая из заменяемых нулями или откидываемых цифр 5, то последняя из оставшихся цифр увеличивается на 1;

3) если отвергаем цифра = 5 со следующими нулями, то округление производится до ближнего четного числа.

Результаты измерения можно записать некоторыми значимыми цифрами и рядом нулей, но в этом случае и нули должны полностью определенное значение и характеризуют погрешность измерения. Н., пусть результат измерения их = 9,5 B, который можно записать цифрами: 9,5; 9,50; 9,500. В этих случаях нули после последней значащей цифры определяют показатель достоверности результатов измерения. С этой точки зрения эти записи необходимо читать так: 9,45

worldofscience.ru

2. Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности. (Например, результат 85.6342, погрешность 0.01. Результат округляют до 85.63. Тот же результат при погрешности в пределах 0.012 следует округлить до 85.634).

3. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним — двумя лишними знаками.

4. Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление приводит к ошибкам.

При округлении числовых значений погрешности и результата измерений необходимо руководствоваться следующими общими правилами округления.

Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. (Например, число 165245 при сохранении четырех значащих цифр округляется до 165200, а число 165.245 — до 165.2).

Если десятичная дробь оканчивается нулями, они отбрасываются только до разряда, который соответствует разряду погрешности. (Например, результат измерений 235.200, погрешность 0.05. Результат округляют до 235.20. Тот же результат при погрешности в пределах 0.015 следует округлить до 235.200).

Если первая (считая слева направо) из заменяемых нулями или отбрасываемых цифр меньше 5, остающиеся цифры не изменяются.

Если первая из этих цифр равна 5, а за ней не следует никаких цифр, или идут нули, то, если последняя цифра в округляемом числе четная или нуль, она остается без изменения, если нечетная — увеличивается на единицу. (Например, число 1234.50 округляют до 1234, а число 8765.50 — до 8766).

Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается на единицу. (Например, число 6783.6 при сохранении четырех значащих цифр, округляют до 6784, а число 12.34520 — до 12.35).

Особенно внимательно следует относиться к записи результата измерения без указания погрешности, так как записи результата 2.4 10 3 В и 2400В не являются тождественными. Первая запись означает, что верны цифры тысяч и сотен вольт и истинное значение может находиться в интервале от 2.351кВ до 2.449кВ. Запись 2400 означает, что верны и единицы вольт, следовательно истинное значение напряжения может находиться в интервале от 2399.51В до 2400.49В.

Поэтому запись результата без указания погрешности крайне нежелательна.

Окончательно правила записи результата измерений можно сформулировать следующим образом.

1) При промежуточных вычислениях значения погрешности сохраняют три -четыре значащие цифры.

2) Окончательное значение погрешности и значение результата округляются в соответствии с изложенными выше правилами.

3) При однократных технических измерениях когда учитывается только основная погрешность СИ (СИ используются в нормальных условиях эксплуатации), результат записывается в виде:

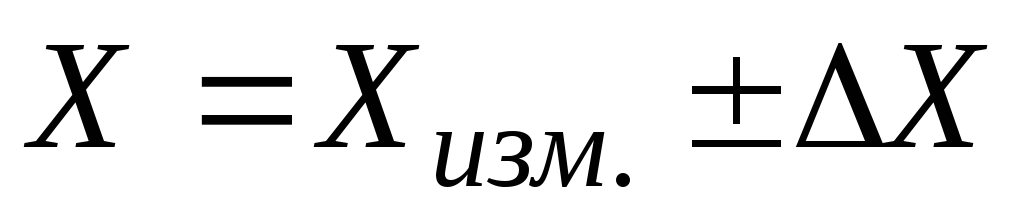или

.

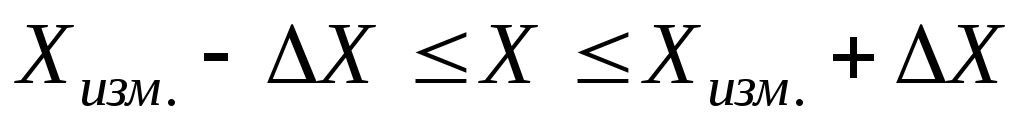(Например, результат измерения напряжения В, погрешность В. Результат может быть записан в виде:)

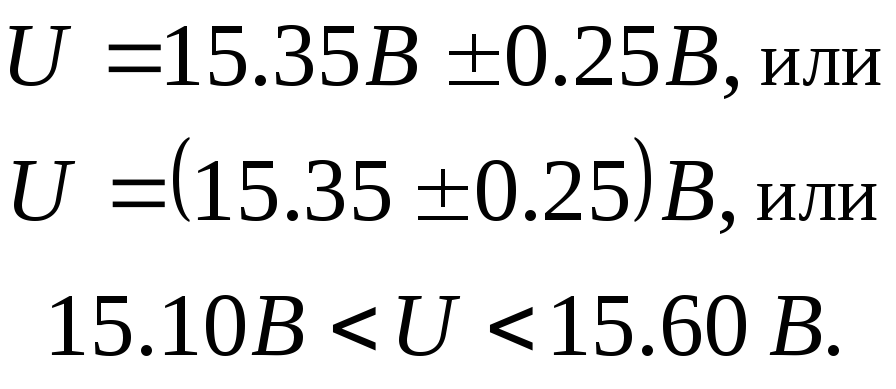
4) При однократных технических измерениях в рабочих условиях, когда по нормативным данным на СИ учитывают основную и дополнительные погрешности и результирующую погрешность определяют по формуле (1.35), результат записывают в виде:

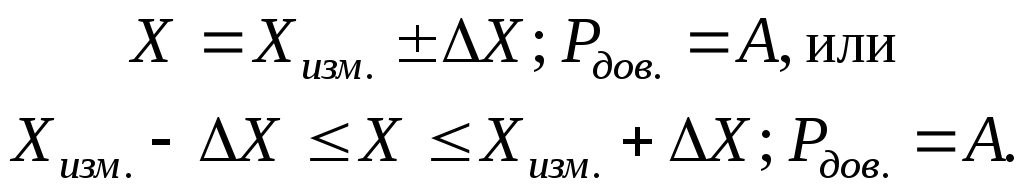
5) При статистических измерениях, когда определяется только величина случайной погрешности нормально распределенных данных в виде доверительного интервала, результат записывается в соответствии с (1.31):

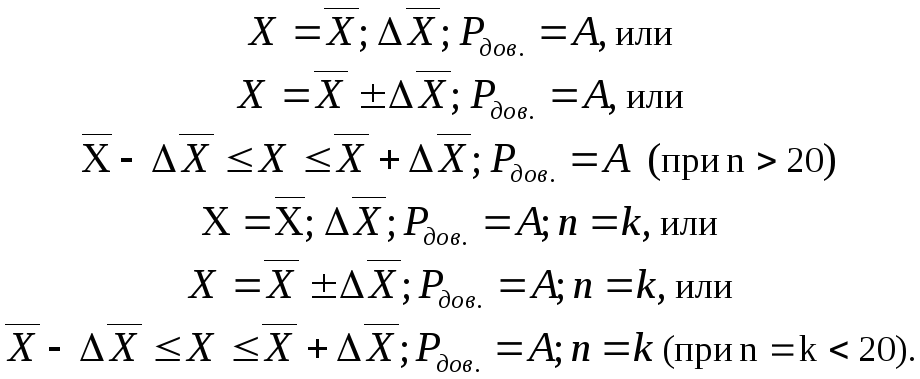
Если границы доверительного интервала несимметрична, то они указываются по отдельности.

6) При статистических измерениях, когда оцениваются границы неисключенных систематических погрешностей результата (НСП) и доверительный интервал случайной погрешности нормально распределенных данных, но результат используется как промежуточный для нахождения других величин (например, при статистических косвенных измерениях) или предполагается сопоставление его с другими результатами аналогичного измерительного эксперимента, результат записывается в соответствии с (1.39):

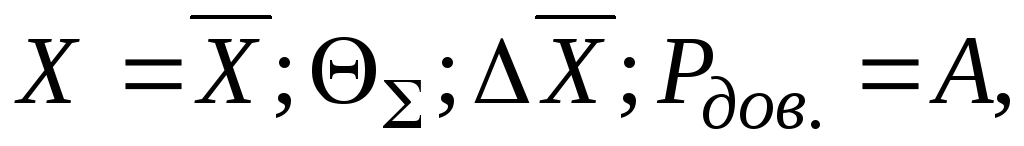
если , то это указывается дополнительно, как в п. 5.

Если границы НСП или границы доверительного интервала несимметричны, то они указываются по отдельности:

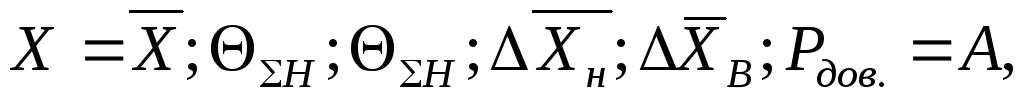
7) Если при измерении получены оценки погрешности при условиях, оговоренных в п. 6, но результат является окончательным и не предполагается в дальнейшем анализ его и сопоставление с другими результатами, то он записывается в соответствии с (1.41):

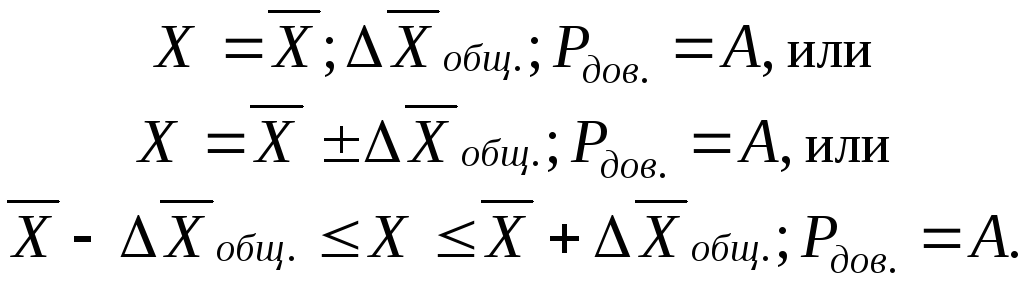
где 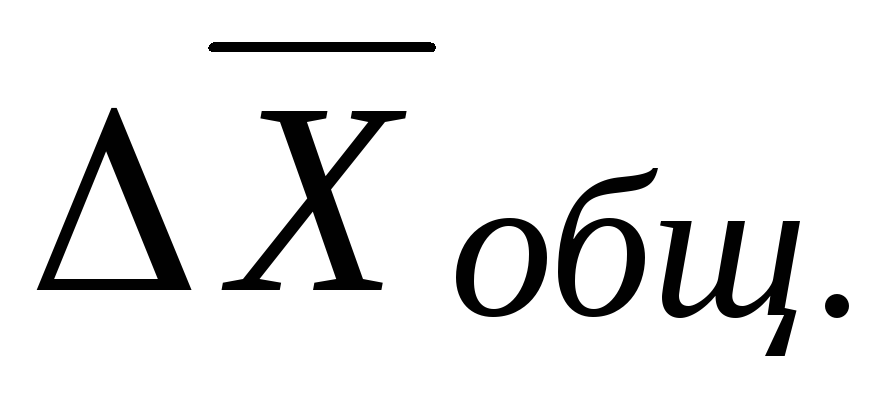определяется по формуле (1.40),

если же , это указывается дополнительно, как в п. 5.

8) При статистических измерениях, когда оцениваются границы НСП и доверительный интервал случайной погрешности, но при обработке результатов идентифицирован закон распределения, отличный от нормального, оценки значения результата измерения и доверительный интервал случайной погрешности находятся по соответствующим формулам [5], результат представляется в виде аналогичном представлению результата в п. 6, но дополнительно приводится информация о виде закона распределения опытных данных.

9) Если как в п. 8 обрабатываются результаты статических измерений и заранее известно, что закон распределения опытных данных отличается от нормального, но действий по идентификации вида реального закона по какой-либо причине не предпринимается, то результат может быть представлен в виде, аналогичном представлению результата в п. 6, но доверительный интервал случайной погрешности определяется в соответствии с рекомендациями ГОСТ 11.001-73 как 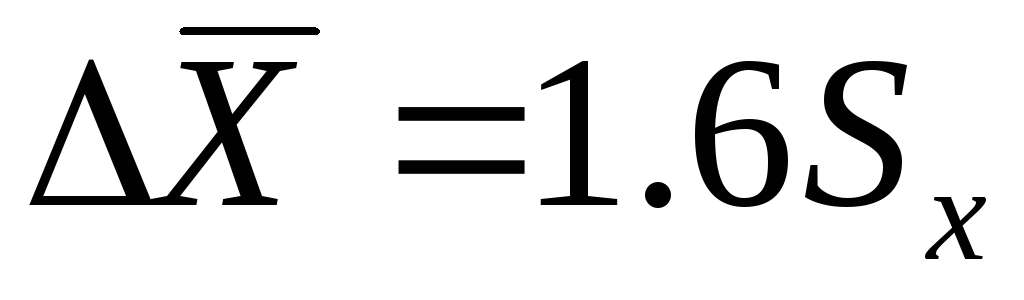при доверительной вероятности .

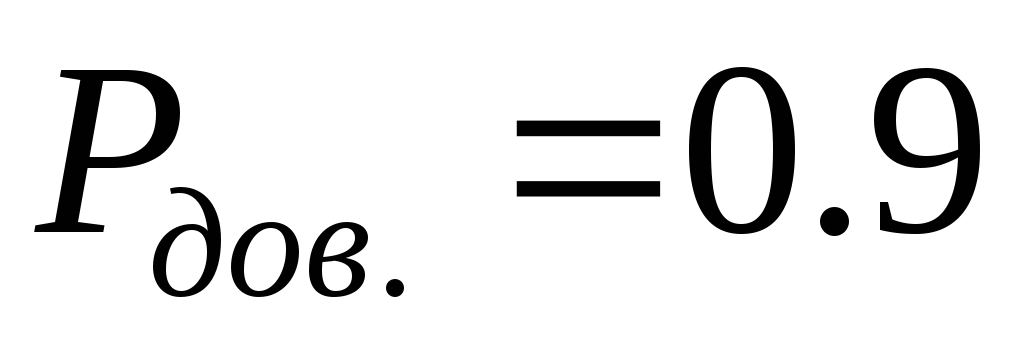Запись результата может выглядеть, например, так:

(при ); ; ; .

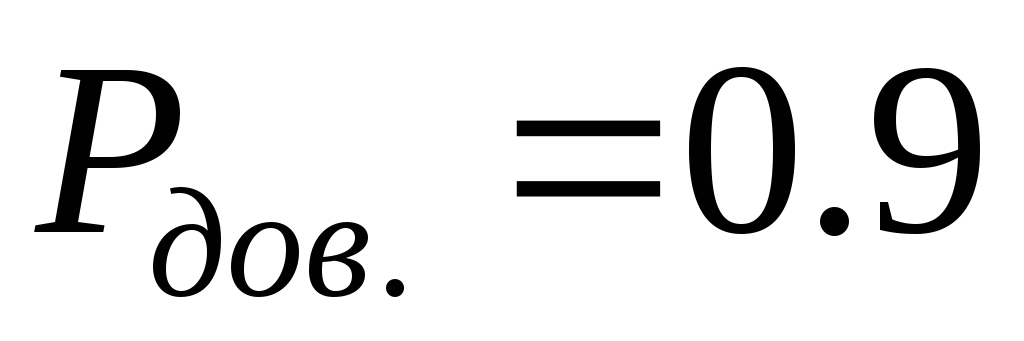Доверительная вероятность, при которой определяется суммарный НСП — , в этом случае может отличаться от .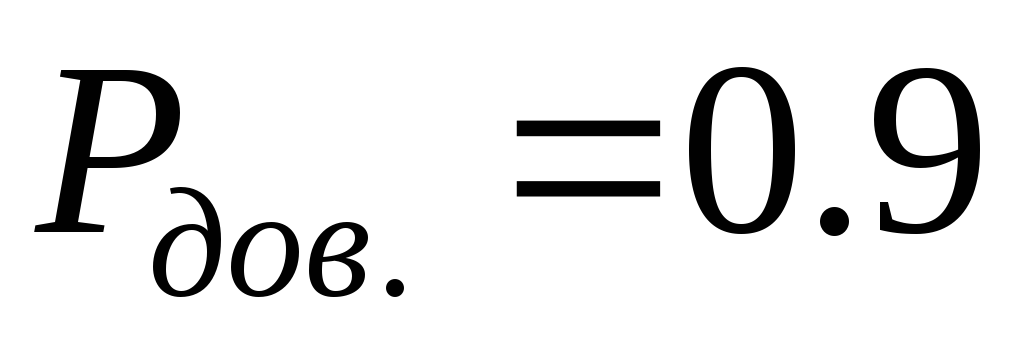

studfiles.net

Значащие цифры правило округления

В приближенных вычислениях часто приходится округлять числа как приближенные, так и точные, т. е. отбрасывать одну или несколько последних цифр. Чтобы обеспечить наибольшую близость округленного числа к округляемому, соблюдаются следующие правила.

Правило 1. Если первая из отбрасываемых цифр больше, чем 5, то последняя из сохраняемых цифр усиливается, т. е. увеличиваемая на единицу. Усиление совершается и тогда, когда первая из отбрасываемых цифр равна 5, а за ней есть одна или несколько значащих цифр. (О случае, когда за отбрасываемой пятеркой нет цифр, см. ниже, правило 3.)

Пример 1. Округляя число 27,874 до трех значащих цифр, пишем 27,9. Третья цифра 8 усилена до 9, так как первая отбрасываемая цифра 7 больше чем 5. Число 27,9 ближе к данному, чем неусиленное округленное число 27,8.

Пример 2. Округляя число 36,251 до первого десятичного знака, пишем 36,3. Цифра десятых 2 усилена до 3, так как первая отбрасываемая цифра равна 5, а за ней есть значащая цифра 1. Число 36,3 ближе к данному (хотя и незначительно), чем неусиленное число 36,2.

Правило 2. Если первая из отбрасываемых цифр меньше чем 5, то усиления не делается.

Пример 3. Округляя число 27,48 до единиц, пишем 27. Это число ближе к данному, чем 28.

Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т. е. последняя сохраняемая цифра оставляется неизменной, если она четная, и усиливается, если она нечетная. Почему применяется это правило, сказано ниже (см. замечание).

Пример 4. Округляя число 0,0465 до третьего десятичного знака, пишем 0,046. Усиления не делаем, так как последняя сохраняемая цифра 6 — четная. Число 0,046 столь же близко к данному, как 0,047.

Пример 5. Округляя число 0,935 до второго десятичного знака, пишем 0,94. Последняя сохраняемая цифра 3 усиливается, так как она нечетная.

Пример 6. Округляя числа 6,527; 0,456; 2,195; 1,450; 0,950; 4,851; 0,850
до первого десятичного знака, получаем:
6,5; 0,5; 2,2; 1,4; 1,0; 4,9; 0,8.

Замечание. Применяя правило 3 к округлению одного числа, мы не увеличиваем точность округления (см. примеры 4 и 5). Но при многочисленных округлениях избыточные числа будут встречаться примерно столь же часто, как недостаточные. Взаимная компенсация погрешностей обеспечит наибольшую точность результата.

www.maths.yfa1.ru