Обобщенный закон Гука

Законом Гука обычно называют линейные соотношения между компонентами деформаций и компонентами напряжений.

Возьмем элементарный прямоугольный параллелепипед с гранями, параллельными координатным осям, нагруженный нормальным напряжением σ_х, равномерно распределенным по двум противоположным граням (рис. 1). При этом σ_y = σ_z = τ_хy = τ_хz = τ_yz = 0.

Вплоть до достижения предела пропорциональности относительное удлинение дается формулой

где Е — модуль упругости при растяжении. Для стали Е = 2*10 5 МПа, поэтому деформации очень малы и измеряются в процентах или в 1*10 5 (в тензометрических приборах, измеряющих деформации).

Удлинение элемента в направлении оси х сопровождается его сужением в поперечном направлении, определяемом компонентами деформаций

где μ – константа, называемая коэффициентом поперечного сжатия или коэффициентом Пуассона. Для стали μ обычно принимается равным 0,25–0,3.

Если рассматриваемый элемент нагружен одновременно нормальными напряжениями σ_x, σ_y, σ_z, равномерно распределенными по его граням, то добавляются деформации

Производя наложение компонент деформации, вызванных каждым из трех напряжений, получим соотношения

Эти соотношения подтверждаются многочисленными экспериментами. Примененный метод наложения или суперпозиции для отыскания полных деформаций и напряжений, вызванных несколькими силами, является законным, пока деформации и напряжения малы и линейно зависят от приложенных сил. В таких случаях мы пренебрегаем малыми изменениями размеров деформируемого тела и малыми перемещениями точек приложения внешних сил и основываем наши вычисления на начальных размерах и начальной форме тела.

Следует отметить, что из малости перемещений еще не следует линейность соотношений между силами и деформациями. Так, например, в сжатом силами Q стержне, нагруженном дополнительно поперечной силой Р, даже при малом прогибе δ возникает дополнительный момент М = Qδ, который делает задачу нелинейной. В таких случаях полные прогибы не являются линейными функциями усилий и не могут быть получены с помощью простого наложения (суперпозиции).

Экспериментально установлено, что если касательные напряжения действуют по всем граням элемента, то искажение соответствующего угла зависит только от соответствующих компонентов касательного напряжения.

Константа G называется модулем упругости при сдвиге или модулем сдвига.

Общий случай деформации элемента от действия на него трех нормальных и трех касательных компонентов напряжений можно получить с помощью наложения: на три линейные деформации, определяемые выражениями (5.2а), накладываются три деформации сдвига, определяемые соотношениями (5.2б). Уравнения (5.2а) и (5.2б) определяют связь между компонентами деформаций и напряжений и называются обобщенным законом Гука. Покажем теперь, что модуль сдвига G выражается через модуль упругости при растяжении Е и коэффициент Пуассона μ. Для этого рассмотрим частный случай, когда σ_х = σ, σ_y = –σ и σ_z = 0.

Вырежем элемент abcd плоскостями, параллельными оси z и наклоненными под углом 45° к осям х и у (рис. 3). Как следует из условий равновесия элемента 0bс, нормальные напряжения σ_v на всех гранях элемента abcd равны нулю, а касательные напряжения равны

Такое напряженное состояние называется чистым сдвигом. Из уравнений (5.2а) следует, что

то есть удлинение горизонтального элемента 0c равно укорочению вертикального элемента 0b: ε_y = –ε_x.

Угол между гранями аb и bc изменяется, и соответствующую величину деформации сдвига γ можно найти из треугольника 0bс:

Отсюда следует, что

и при малых γ получим

Отсюда и, следовательно,

Уравнения (5.2а) и (5.2б) определяют компоненты деформаций через компоненты напряжений. Выведем обратные соотношения — напряжения через деформации.

Складывая уравнения (5.2а) и используя обозначения

получаем зависимость между средней деформацией и средним напряжением

Поскольку Зε₀ равно объемному расширению, величину называют модулем объемного расширения. Используя соотношения (5.4) и решая уравнения (5.2а) относительно σ_х, σ_у, σ_z, получим

Если учесть, что , то закон Гука запишется в виде

Тогда соотношения (4.11) можно записать в виде

Если ввести символ Кронекера , то закон Гука в краткой записи примет вид

vse-lekcii.ru

Лекция 3. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В ГРУНТЕ ФАЗЫ ДЕФОРМАЦИЙ ГРУНТА ПОД ФУНДАМЕНТОМ

в рамках общей темы «Напряженное состояние грунтов в допредельном и предельном состояниях»

Решение задачи определения напряжений в грунте необходимо для установления условий прочности и устойчивости грунтов и определения их деформаций (например, осадок). При решении вопроса о распределении напряжений в грунтах в Механике грунтов применяют теорию линейно-деформируемых тел. То есть для определения напряжений могут быть применены уравнения и зависимости теории упругости, базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука). Однако при применении закона Гука для грунтов необходимо условиться об ограничениях, поскольку в грунтах возникают не только упругие, но значительные остаточные деформации.

ОБЩАЯ ЗАВИСИМОСТЬ МЕЖДУ ДЕФОРМАЦИЯМИ И НАПРЯЖЕНИЯМИ. ПРИНЦИП ЛИНЕЙНОЙ ДЕФОРМИРУЕМОСТИ

В основу теории распределения напряжений в грунтах кладётся зависимость между относительными деформациями ε и нормальными напряжениями.

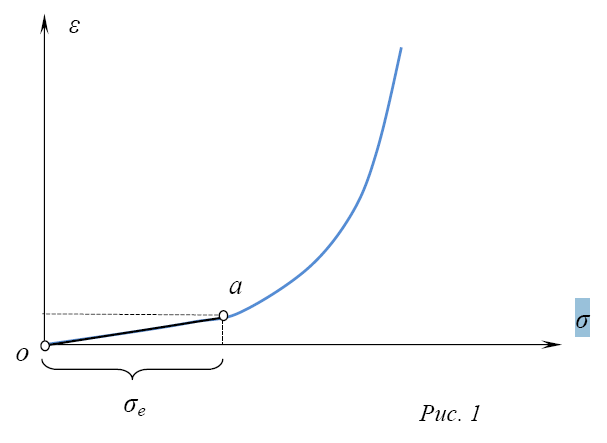
В общем случае (согласно опытам) зависимость между деформациями и напряжениями для грунтов будет нелинейной: σ

Однако в определенном интервале напряжений (при не очень больших изменениях внешних давлений – порядка 1÷3 кг/см 2 ) с достаточной для практических целей точностью зависимость между деформациями ε и нормальными напряжениями σ может приниматься линейной (спрямлённый участок оа на кривой, рис. 1).

Сформулируем принцип линейной деформируемости для грунтов: при небольших изменениях давлений грунты можно рассматривать как линейно-деформируемые тела, то есть зависимость между общими деформациями и напряжениями для грунтов может быть принята линейной: σ = Е · ε.

НАПРЯЖЕНИЕ, ПЕРЕДАВАЕМОЕ ГРУНТУ ПО ПОДОШВЕ ФУНДАМЕНТА

Это напряжение не остается по глубине постоянным, а в некоторой области грунтовой толщи рассеивается. Для решения задач о распределении напряжений применяют уравнения теории упругости, рассматривая грунты как тела однородные, изотропные и линейно-деформируемые, подчиняющиеся закону Гука. Для оснований гражданских и промышленных зданий назначают такую величину допустимых напряжений, при которой в грунте не возникают пластические (остаточные) деформации.

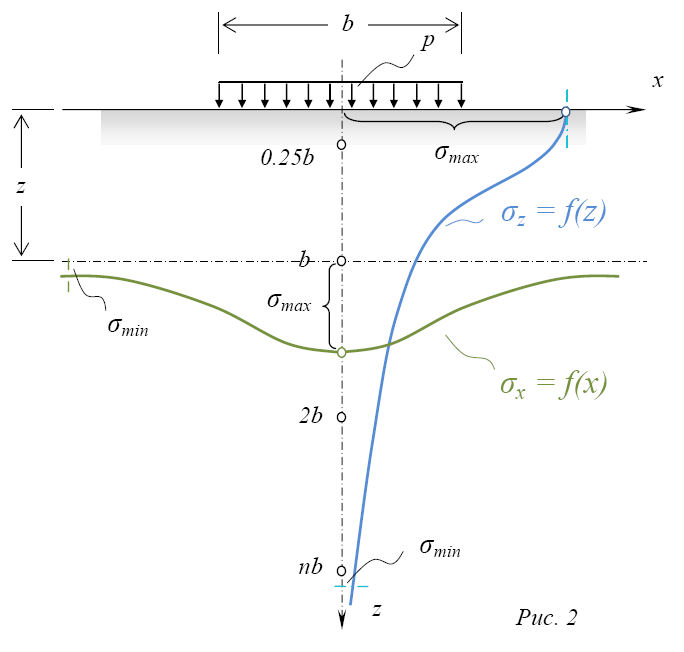
Изменение напряжений σ по различным вертикальным (z) и горизонтальным (x) сечениям характеризуется эпюрами σ_z и σ_x (рис. 2). Как видно из рисунка, напряжения в грунтовой толще изменяются, как непрерывные функции от σ_max до σ_min как по вертикальному, так и по горизонтальному направлению.

В напряженной зоне грунта имеются точки с одинаковыми напряжениями, через которые можно провести линии (т.н. кривые равных напряжений). Например, линии, проходящие через точки с одинаковым вертикальным напряжением σ_z, называются изобарами. В сжимаемой толще можно провести какое угодно число изобар (в зависимости от того, какие по величине напряжения соединяются линиями). Например, если к поверхности грунта приложена распределенная полосовая нагрузка интенсивностью p, то семейство изобар будет выглядеть следующим образом:

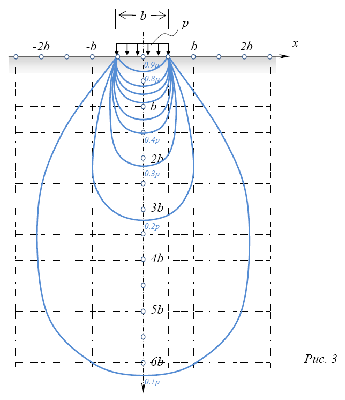
Семейство изобар принято называть «луковицей напряжений». Построение «луковиц напряжений» полезно при оценке напряженного состояния в основаниях сооружений: подобное изображение наглядно иллюстрирует изменение напряжений в грунте под нагрузкой.

ФАЗЫ ДЕФОРМАЦИЙ ГРУНТА ПОД ФУНДАМЕНТОМ

Закономерность нарастания осадок с постепенным увеличением статической нагрузки характеризуется графиком:

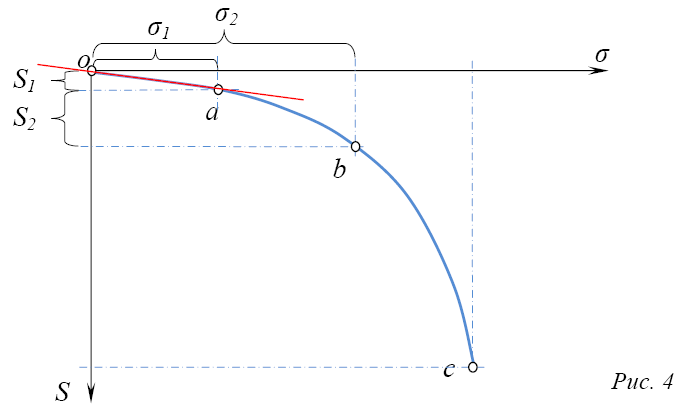
Этот график имеет три характерных участка (oa, ab и bc на графике, рис. 4).

Начальный участок о имеет пологое очертание и согласно принципу линейной деформируемости может быть заменён прямой. Деформация на участке прямой называется фазой уплотнения (рис. 5).

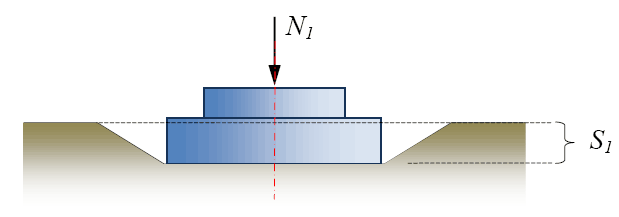
Рис. 5. Фаза уплотнения

В фазе уплотнения происходит более плотная укладка частиц грунта за счёт уменьшения объёма пор. Ни в одной точке основания касательные напряжения по своей величине не превосходят сил внутреннего сопротивления грунта сдвигу, то есть повсюду существует состояние устойчивого равновесия грунта (τ τ_пр) и выпирания его из-под фундамента. Деформация на участке bc называется фазой выпирания (рис. 7).

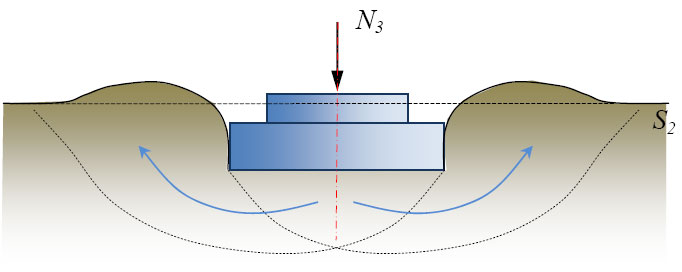
Рис. 7. Фаза выпирания

Таким образом, при возрастании нагрузки на грунт необходимо различать две характерные её величины, при достижении которых резко меняется поведение грунта:
— первую, соответствующую началу перехода фазы уплотнения в фазу сдвигов – то есть фазу зарождения и развития зон предельного напряженного состояния;
— и вторую, когда исчерпывается несущая способность грунтового основания и наблюдается полное развитие зон предельного равновесия, при котором даже весьма незначительное увеличение нагрузки приводит грунт к потере прочности и устойчивости (к разрушению).

zimbelmann.ru

Закон гука для грунтов

1.12. Сила упругости. Закон Гука

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости .

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

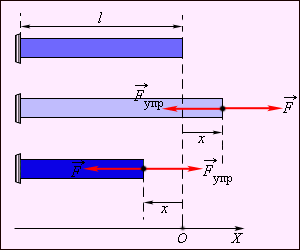
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).

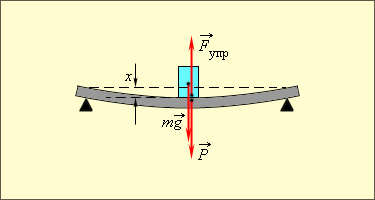
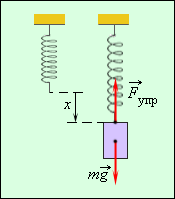
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры . При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления . Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины . В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром . Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 % . При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

physics.ru

ЗАКОН ГУКА

Научно-технический энциклопедический словарь .

Смотреть что такое «ЗАКОН ГУКА» в других словарях:

закон Гука — Закон, устанавливающий пропорциональность между напряжением и деформацией (см. elastic constant) [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN Hooke s law … Справочник технического переводчика

Закон Гука — – основной закон, устанавливающий в известных пределах прямолинейную зависимость между напряженным состоянием и деформацией упругого тела. [Большая советская энциклопедия. М.: Советская энциклопедия. 1969 1978.] Рубрика термина: Теория и… … Энциклопедия терминов, определений и пояснений строительных материалов

ЗАКОН ГУКА — закон, устанавливающий линейную зависимость между (см.) твёрдого тела и приложенным механическим напряжением. Согласно З. Г. сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную… … Большая политехническая энциклопедия

Закон Гука — Механика сплошных сред … Википедия

закон Гука — [Hooke s law] упругая деформация материала прямо пропорциональна приложенному напряжению: εн = σ/Е (для одноосного растяжения) и γ = τ/G (для сдвига), где εн относительная продольная деформация (Δl/l); ΔТ относительный сдвиг; σ нормальное… … Энциклопедический словарь по металлургии

Закон Гука — Hooke s law Закон Гука. Обобщение, применимое ко всем твердым материалам, которое показывает, что напряжение прямо пропорционально деформации и выражается как Е = constant = σ/ε = Напряжение/деформация, где Е модуль упругости (Юнга). Постоянное… … Словарь металлургических терминов

закон Гука — Huko dėsnis statusas T sritis fizika atitikmenys: angl. Hooke’s law vok. Hookesches Gesetz, n rus. закон Гука, m pranc. loi de Hooke, f … Fizikos terminų žodynas

Закон Гука — основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (1635 1703) в 1660 г. При растяжении стержня длиной l его удлинение пропорционально растягивающей силе… … Концепции современного естествознания. Словарь основных терминов

закон гука для рiдини при всесторонньому стисненнi — закон Гука для жидкости при всестороннем сжатии Hooke’s law for liquid in all round compression Hookesches Gesetz für die Flüssigkeit bei allseitiger Kompressibilität – змiна об’єму рiдини V при всесторонньому стисненнi прямо пропорцiйна змiнi… … Гірничий енциклопедичний словник

обобщенный закон Гука — [generalized Hooke s law] устанавливает линейную связь между напряжениями и деформациями в любых направлениях, т.е. между каждым компонентом тензора напряжений и каждым компонентом тензора деформаций: εx = [σx μ(σy σz)]E; γxy = τxy/G; εy = [σy… … Энциклопедический словарь по металлургии

dic.academic.ru

Размещено на реф.рф
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, сжимаемостью грунта принято называть его способность уменьшаться в объёме (деформироваться) от внешней нагрузки.

Грунт состоит из твердых частиц и пор, которые частично или полностью заполнены водой. Поскольку напряжения сжатия, возникающие обычно в основаниях зданий и сооружений, сравнительно небольшие, так как объёмные деформации твердых частиц (кварца, полевого шпата и др.) ничтожно малы и их не учитывают, то можно считать, что изменение объёма грунта при сжатии происходит только из-за изменения объёма его пор.

Сжимаемость грунта зависит от его пористости, гранулометрического и минœералогического составов, природы внутренних структурных связей и характера нагрузки.

Сжимаемость грунтов обусловливается следующими причинами:

· уменьшением пористости грунтов под воздействием внешних нагрузок вследствие переупаковки твердых частиц;

· уменьшением толщины водно-коллоидных оболочек минœеральных частиц под влиянием увеличивающегося внешнего давления;

· изменением физического состояния.

Сжатие грунтов под нагрузкой принято называть осадкой, или деформацией, грунтов.

Деформации грунтов имеют упругий и пластический характер.

Размещено на реф.рф
Упругие деформации возникают под действием нагрузок, не превышающих структурной прочности грунта. При снятии таких нагрузок происходит восстановление деформаций.

В случае если нагрузки превышают структурную прочность грунта͵ то связи между частицами (скелœет грунта) разрушаются. Возникают так называемые пластические деформации, которые вызваны относительным перемещением частиц. Скорость развития пластических деформаций зависит от вида грунта͵ к примеру, в песках крупных и средней крупности, крупнообломочных и трещиноватых скальных грунтах она на несколько порядков выше, чем в глинистых.

В свою очередь пластические деформации в грунтах можно разделить на объёмные и сдвиговые. Объемные деформации приводят к изменению объёма пор в грунте, ᴛ.ᴇ. его уплотнению, а сдвиговые — к изменению его первоначальной формы и могут вызывать разрушение грунта.

Основными характеристиками сжимаемости грунтовявляются модуль общей деформации Е или коэффициент относительной сжимаемости m_v, коэффициент поперечного расширения (коэффициент Пуассона) v и коэффициент бокового давления ξ грунта.

Испытание грунтов на сжатие производится следующими видами:

· одноосное сжатие образцов;

и формулируется так: отношение приращений коэффициента пористости и давления есть величина постоянная, равная коэффициенту сжимаемости с обратным знаком.

Коэффициент сжимаемости — расчетная характеристика деформируемости фунтов, которая используется при определœении осадок сооружений. С помощью этого коэффициента можно производить качественную оценку грунта как основания зданий и сооружений:

при m₀≤0,1 Мпа -1 – грунт мало сжимаемый,

0,1≤m₀≤1,0 Мпа -1 – средней сжимаемости,

m₀>1,0 Мпа -1 – сильно сжимаемый.

Для установления базовых показателœей сжимаемости грунтов производятся их испытания на уплотнение под нагрузкой, когда деформации грунта могут развиваться только в одном направлении и никакие другие силы, кроме внешней нагрузки, не действуют.

Испытанияобразцов на одноосное сжатие являются простейшими и применяются для прочных скальных, полускальных, мерзлых и плотных глинистых грунтов, из которых можно вырезать образец цилиндрической и призматической формы с диаметром или стороной поперечного сечения 40-45 мм (рис.). Особенностью такого испытания является отсутствие боковых напряжений (σ_х=σ_у=0), ᴛ.ᴇ. возможность свободных боковых деформаций грунта (ε_х=ε_у-∞). Согласно рис. относительная деформация образца грунта

Рис. Испытание грунта на одноосное сжатие: а — схема испытания; б — диаграмма деформаций

Связь между напряжением и деформацией устанавливается согласно известному из сопротивления материалов закону Гука σ=εЕ, где Е – модуль упругости грунта.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, испытание грунта на одноосное сжатие в наименьшей степени соответствует действительным условиям деформирования грунта в массиве, так как не учитывает реакции окружающего его грунта͵ который ограничивает боковые перемещения.

Компрессионные испытания – наиболее распространенный вид лабораторных исследований для определœения деформационных характеристик (свойств) грунтов. Компрессия — ϶ᴛᴏ процесс сжатия фунта без возможности бокового расширения (εх=εy=0), ᴛ.ᴇ. уплотнение образца без его разрушения.

Компрессионные испытания грунтов в лабораторных условиях проводятся в компрессионных приборах (одометрах).

Одометр − прибор, служащий для определœения сжимаемости грунта. Деформации в одометре возможны только в вертикальном направлении, горизонтальные деформации отсутствуют. Вертикальное напряжение изменяется ступенями и является известным, боковые напряжения реактивные и остаются неизвестными.

Конструкции их бывают различные, исходя из способа приложения нагрузки и целœей исследования.

На компрессионное сжатие образец грунта испытывается в металлическом кольце, и на него через жесткий штамп передается сила F, вызывающая в образце сжимающее напряжение σ = F/A, где А – площадь поперечного сечения образца. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, под действием вертикальной нагрузки происходит вертикальное перемещение штампа, вызывающее осадку образца.

referatwork.ru