1.Основные понятия

Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году. По своей значимости они аналогичны законам Ньютона в механике. Современная формулировка дана Герцем и Хевисайдом. Эти уравнения связывают характеристики электромагнитного поля и его источники.

В данные уравнения входят — напряженность электрического поля, индукция магнитного поля. Эти величины являются основными, т.к. определяют силу, действующую на заряженную частицу (Fл) – силу Лоренца.

Входят две вспомогательные величины — индукция электрического поля и — напряженность магнитного поля. Также входят — плотность тока и ρ — плотность заряда.

Уравнения Максвелла позволяют по известному полю найти токи и заряды (достаточно просто), а также по известным токам и зарядам найти поле (сложно). Уравнения будем писать в СИ в порядке указанном в физической энциклопедии.

2.Интегральная форма

I уравнение представляет собой обобщение закона полного тока.

II уравнение обобщает закон электромагнитной индукции.

III уравнение: теорема Гаусса для электрической индукции.

IV уравнение: закон Гаусса для индукции магнитного поля.

Закон: Поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю.

3.Дифференциальная форма

Используя формулы Остроградского-Гаусса и Стокса можно получить

I уравнение Максвелла.

II уравнение Максвелла.

III уравнение Максвелла.

IV уравнение Максвелла

4.Материальные уравнения

В систему уравнений Максвелла входят 16 скалярных функций координат и времени. Самих уравнений – 8.

Чтобы замкнуть эту систему, используют материальные уравнения.

Величины e, μ, σ получаются из других разделов физики или определяются экспериментально.

tsput.ru

Уравнение токов закон

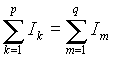, где p+q=n.

Очевидно, что обе формулировки равноценны и выбор формы записи уравнений может быть произвольным. Существенным является только соглашение о знаках токов для данной цепи, т.е. в пределах описания одной электрической цепи нельзя для разных узлов использовать разные знаки для токов направленных к узлам или от узлов .

При составлении уравнений по первому закону Кирхгофа направления токов в ветвях электрической цепи выбирают обычно произвольно. При этом необязательно даже стремиться, чтобы во всех узлах цепи присутствовали токи разных направлений. Может получиться так, что в каком-либо узле все токи сходящихся в нем ветвей будут направлены к узлу или от узла, нарушая тем самым принцип непрерывности. В этом случае в процессе определения токов один или несколько из них окажутся отрицательными, что будет свидетельствовать о протекании их в направлении противоположном принятому.

Второй закон Кирхгофа связан с понятием потенциала электрического поля, как работы, совершаемой при перемещении единичного точечного заряда в пространстве. Если такое перемещение совершается по замкнутому контуру , то суммарная работа при возвращении в исходную точку будет равна нулю. В противном случае путем обхода контура можно было бы получать положительную энергию, нарушая закон ее сохранения.

Каждый узел или точка электрической цепи обладает собственным потенциалом и, перемещаясь вдоль замкнутого контура, мы совершаем работу, которая при возврате в исходную точку будет равна нулю. Это свойство потенциального электрического поля и описывает второй закон Кирхгофа в применении к электрической цепи.

Он также как и первый закон формулируется в двух вариантах, связанных с тем, что падение напряжения на источнике ЭДС численно равно электродвижущей силе, но имеет противоположный знак. Поэтому, если какая либо ветвь содержит сопротивление и источник ЭДС, направление которой согласно с направлением тока, то при обходе контура эти два слагаемых падения напряжения будут учитываться с разными знаками. Если же падение напряжения на источнике ЭДС учесть в другой части уравнения, то его знак будет соответствовать знаку напряжения на сопротивлении.

Сформулируем оба варианта второго закона Кирхгофа , т.к. они принципиально равноценны:

  • алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю

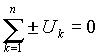
    • Примечание: знак + выбирается перед падением напряжения на резисторе, если направление протекания тока через него и направление обхода контура совпадают; для падений напряжения на источниках ЭДС знак + выбирается, если направление обхода контура и направление действия ЭДС встречны независимо от направления протекания тока;


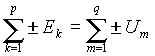    • алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжения на резисторах в этом контуре

    , где p+q=n

    Примечание: знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.

    Здесь также как и в первом законе оба варианта корректны, но на практике удобнее использовать второй вариант, т.к. в нем проще определить знаки слагаемых.

    С помощью законов Кирхгофа для любой электрической цепи можно составить независимую систему уравнений и определить любые неизвестные параметры, если число их не превышает число уравнений. Для выполнения условий независимости эти уравнения должны составляться по определенным правилам.

    Общее число уравнений N в системе равно числу ветвей N в минус число ветвей, содержащих источники тока N J , т.е. N = N в — NJ .

    Наиболее простыми по выражениям являются уравнения по первому закону Кирхгофа, однако их число N 1 не может быть больше числа узлов Nу минус один.
    Недостающие уравнения составляются по второму закону Кирхгофа, т.е.

    Сформулируем алгоритм составления системы уравнений по законам Кирхгофа :

  1. определить число узлов и ветвей цепи Nу и N в ;
  2. определить число уравнений по первому и второму законам N 1 и N 2 . ;
  3. для всех ветвей (кроме ветвей с источниками тока) произвольно задать
    направления протекания токов;
  4. для всех узлов, кроме одного, выбранного произвольно, составить уравнения по первому закону Кирхгофа;
  5. произвольно выбрать на схеме электрической цепи замкнутые контуры таким образом, чтобы они отличались друг от друга по крайней мере одной ветвью и чтобы все ветви, кроме ветвей с источниками тока, входили по крайней мере в один контур;
  6. произвольно выбрать для каждого контура направление обхода и составить уравнения по второму закону Кирхгофа, включая в правую часть уравнения ЭДС действующие в контуре, а в левую падения напряжения на резисторах. Примечание: Знак ЭДС выбирают положительным, если направление ее действия совпадает с направлением обхода независимо от направления тока; а знак падения напряжения на резисторе принимают положительным, если направление тока в нем совпадает с направлением обхода.

Рассмотрим этот алгоритм на примере рис 2.

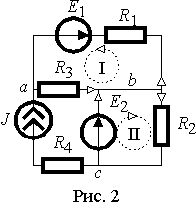
Здесь светлыми стрелками обозначены выбранные произвольно направления токов в ветвях цепи. Ток в ветви с R 4 не выбирается произвольно, т.к. в этой ветви он определяется действием источником тока.

Число ветвей цепи равно 5, а т.к. одна из них содержит источник тока, то общее число уравнений Кирхгофа равно четырем.

Число узлов цепи равно трем ( a, b и c ), поэтому число уравнений по первому закону Кирхгофа равно двум и их можно составлять для любой пары из этих трех узлов. Пусть это будут узлы a и b , тогда

de.ifmo.ru

1. Теория: Законы Кирхгофа

В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.

Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.

Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.

Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.

Первый закон Кирхгофа

Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.

Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.

Здесь ток I1 — ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:

Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I 3 в левую часть выражения (1), тем самым получим:

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).

Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E1=12 в и E2=5 в , с внутренним сопротивлением источников r1=r2=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

так как I1 и I 2 втекают в узел А , а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

Для внутреннего левого контура:

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

12 = 0,1I1 +2I.

Далее из первого и второго уравнения выразим ток I2

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

12 = 0,1I1 + 2I.

Выражаем из первого уравнения значение I

I = 2I1– 70;

И подставляем его значение во второе уравнение

Решаем полученное уравнение

12 = 0,1I1 + 4I1 – 140.

12 + 140= 4,1I1

Теперь в выражение I = 2I1– 70 подставим значение

I1=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I2=I — I1

I2=4,146 — 37,073 = -32,927

Знак «минус» для тока I2 означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I 2 вытекает из узла А .

Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.

Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

www.sxemotehnika.ru

Законы Кирхгофа — формулы и примеры использования

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

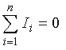
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0

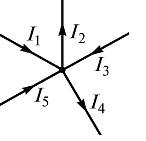
В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

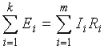
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

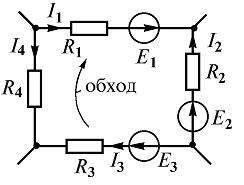
Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

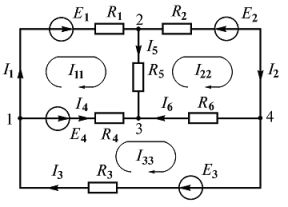
Составляем необходимое число уравнений по первому и второму законам Кирхгофа

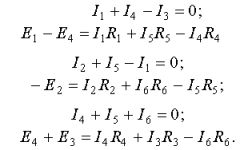
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

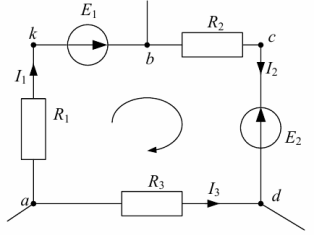
Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

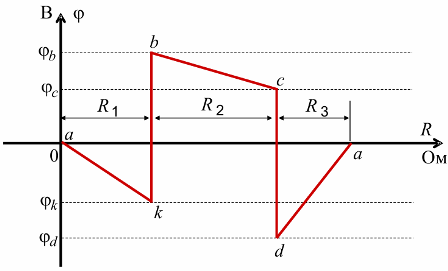
Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

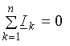
Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

electricalschool.info

§ 2.8. Составление уравнений для расчета токов в схемах с помощью законов Кирхгофа

§ 2.8. Составление уравнений для расчета токов в схемах с помощью законов Кирхгофа. Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы в, число ветвей, содержащих источники тока, — вит и число узлов у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется в — вит. Перед тем как составить уравнения, необходимо произвольно выбрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.

С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, например по часовой стрелке.

Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют уравнения, число которых равно числу узлов без единицы, т. е. у — 1.

Уравнение для последнего у-го узла не составляют, так как оно совпало бы с уравнением, полученным при суммировании уже составленных уравнений для у — 1 узлов, поскольку в эту сумму входили бы дважды и с противоположными знаками токи ветвей, не подходящих к у-му узлу, а токи ветвей, подходящих к у-му узлу, входили бы в эту сумму со знаками, противоположными тем, с какими они вошли бы в уравнение для у-го узла.

По второму закону Кирхгофа составляют уравнения, число которых равно числу ветвей без источников тока (в — вит), за вычетом уравнений, составленных по первому закону Кирхгофа, т. е. (в — вит) — (у — 1) = в — вит — у + 1.

Составляя уравнения по второму закону Кирхгофа, следует охватить все ветви схемы, исключая лишь ветви с источниками тока.

Если попытаться составить уравнение по второму закону Кирхгофа в форме (2.4) для контура, в который входит источник тока, то в него вошли бы бесконечно большие слагаемые и оно не имело бы смысла.

При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры условимся называть независимыми.

Требование, чтобы в каждый новый контур входила хотя бы одна новая ветвь, является достаточным, но не необходимым условием, а потому его не всегда выполняют. В таких случаях часть уравнений по второму закону Кирхгофа составляют для контуров, все ветви которых уже вошли в предыдущие контуры.

Клещи электроизмерительные

Пример 10. Найти токи в ветвях схемы рис. 2.9, в которой Е1 = 80 В, Е2 = 64 В, R1 = 6 Ом, R2 = 4 Ом, R3 = 3 Ом, R4 = 1 Ом.

Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме рис. 2.9, в = 3; вит = 0; у = 2.

Следовательно, по первому закону Кирхгофа, можно составить только одно уравнение:

Нетрудно убедиться, что для второго узла получили бы аналогичное уравнение. По второму закону Кирхгофа составим в — вит — (у — 1) = 3 — 0 — (2 — 1) = 2 уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.

Знак плюс перед I1R1 взят потому, что направление тока совпадает с направлением обхода контура; знак минус перед I2R2 — потому, что направление I2 встречно обходу контура.

Совместное решение уравнений (а) — (в)дает I1 = 14 А, I2 = — 15 А, I3 = — 1 А.

Поскольку положительные направления токов выбирают произвольно, в результате расчета какой-либо один или несколько токов могут оказаться отрицательными. В рассмотренном примере отрицательными оказались токи I2 и I3, что следует понимать так: направления токов I2 и I3 не совпадают с направлениями, принятыми для них на рис. 2.9 за положительные, т. е. в действительности токи I2 и I3 проходят в обратном направлении.

Для выбора контура таким образом, чтобы в каждый из них входило по одной ветви, не входящей в остальные контуры, используют понятие дерева. Поддеревом понимают совокупность ветвей, касающихся всех узлов, но не образующих ни одного замкнутого контура. Из одной и той же схемы можно образовать несколько деревьев. При составлении системы уравнений по второму закону Кирхгофа можно взять любое дерево из возможных.

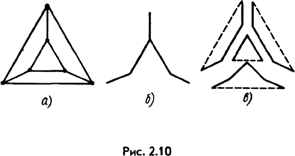
Одно из возможных деревьев схемы рис. 2.10, а изображено на рис. 2.10, б, а на рис. 2.10, в — четыре независимых контура, в каждый из которых входит по одной пунктиром показанной ветви, не входящей в остальные. Более подробно о топологии электрических схем см. § 2.31 — 2.35 и А.5 — А. 10.

www.sonel.ru