Умножение и его свойства

Определение. Умножение — это действие в результате которого находят сумму одинаковых слагаемых. Умножить число а на число Ь означает найти сумму Ь слагаемых, каждое из которых равно а.

Числа, которые перемножаются, называются множителями (или сомножителями), а результат умножения — произведением .

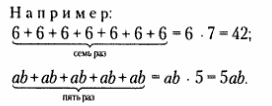
При умножении натуральных чисел произведение всегда число положительное. Если один из множителей равен 0 (нулю), то произведение равно 0. Если произведение равно нулю, то хотя бы один из множителей равен 0.

Если один из двух множителей равен 1 (единице), То произведение равно второму множителю.

• 5 * 6 * 8 * 0 = 0
• 132 * 1 = 132

Сочетательный закон

Правило. Чтобы произведение двух множителей умножить на третий множитель, можно первый множитель умножить на произведение второго и третьего множителей.

• (7 * 6) * 5 = 7 * (6 * 5) = 210
• (a * b) * c = a * (b * c)

Переместительный закон

Правило. От перестановки множителей произведение не изменяется.

• Например:
• 7 * 6 * 5 = 5 * 6 * 7 = 210
• а * Ь * с = с * Ь * а

Распределительным закон

Правило. Чтобы умножить число на сумму, можно умножить это число на каждое из слагаемых и полученные произведения сложить.

• 7 * (6 + 5) = 7 * 6 + 7 * 5 = 77
• a * (b + c) = ab + ac

Распределительный закон распространяется и на действие вычитания.

• 7 * (6 — 5) = 7 * 6 — 7 * 5 = 7

Законы умножении распространяются на любое количество множителей в числовом или буквенном выражении. Распределительный закон умножения используется для вынесения общего множителя за скобки.

Правило. Чтобы преобразовать сумму (разность) в произведение, достаточно вынести за скобки одинаковый множитель слагаемых, а оставшиеся множители записать в скобках суммой (разностью).

• 7 * 8 — 7 * 5 = 7 * (8 — 5)
• аЬ + ас = а * (Ь + с)

Вынесение множителя за скобки для больших числовых или буквенных выражений можно производить по группам слагаемых.

shkolo.ru

Для рациональных чисел остаются справедливыми те же законы умножения, которые были приведены в § 5 для положительных чисел.

1. Переместительный закон.

Для любых рациональных чисел a и b справедливо равенство:

Это следует из определения умножения рациональных чисел. В самом деле, мы берем произведение абсолютных величин сомножителей, а оно не зависит от порядка, в котором берем эти абсолютные величины.

Знак произведения тоже определяем независимо от того, в каком порядке следовали сомножители. Мы смотрим только, одинаковые ли знаки у обоих сомножителей или различные.

Переместительный закон справедлив для произведения любого числа сомножителей. Так, например, перемножая числа –2, 3, 5 и –8 в любом порядке, мы получим одно и то же число 240. В самом деле, в каком бы порядке мы ни перемножали абсолютные величины сомножителей, получим одно и то же число 2 * 3 * 5 * 8 = 240. Знак произведения получим, подсчитав количество отрицательных сомножителей независимо от порядка, в каком они расположены. В нашем примере число 240 следует взять со знаком +, так как в произведении содержится два отрицательных сомножителя.

2. Сочетательный закон.

При умножении любых рациональных чисел остается в силе сочетательный закон умножения.

Для любых трех рациональных чисел a, b и с справедливо равенство:

В самом деле, в выражении a(bc) мы должны абсолютную величину a умножить на произведение абсолютных величин b и c , в выражении (ab)c мы должны произведение абсолютных величин a и b умножить на абсолютную величину c . Но абсолютные величины — это неотрицательные числа (то есть положительные или равные нулю), а для таких чисел сочетательный закон верен.

Значит, абсолютная величина обеих частей равенства одна и та же. Легко также убедиться, что и знак обоих произведений будет один и тот же, каковы бы ни были знаки чисел a, b и с (оба произведения положительны, если среди чисел a, b и с нет отрицательных или два из них отрицательны; оба произведения отрицательны, если одно из этих чисел или все три отрицательны; оба произведения равны нулю, если хотя бы одно из чисел a, b или c равно нулю).

Таким же образом можно убедиться в справедливости сочетательного закона для произведения любого числа сомножителей.

Пример . Это произведение нетрудно вычислить, перемножив сначала второй и третий сомножители: 3. Распределительный закон.

Для любых рациональных чисел a, b и с справедливо равенство:

Убедимся в этом на примерах.

1) [2 + (–3)] * 4 = 2 * 4 + (–3) * 4.

[2 + (–3)] * 4 = (–1) * 4 = –4;
2 * 4 + (–3) * 4 = 8 – 12 = –4.

2) [(–3) + 5] * (–6) = (–3) * (–6) + 5 * (–6).

[(–3) + 5] * (–6) = 2 * (–6) = –12;
(–3) * (–6) + 5 * (–6) = 18 – 30 = –12.

Распределительный закон имеет место при умножении на какой-либо множитель суммы любого числа слагаемых.

Чтобы умножить сумму на какое-либо число, можно умножить на это число каждое слагаемое и полученные произведения сложить.

Пользуясь переместительным законом умножения, в последнем примере можно переставить сомножители, тогда получим следующее:

Чтобы умножить какое-либо число на сумму, можно умножить это число на каждое слагаемое и полученные произведения сложить.

Отметим следующие два свойства умножения:

1. Умножение произведения.
Чтобы умножить произведение нескольких чисел на число, можно умножить на это число один из сомножителей, оставив остальные без изменения.

[4 * (–3) * 5] * (–2) = (–60) * (–2) = 120
и
[4 * (–2)] * (–3) * 5 = (–8) * (–3) * 5 = 120.

2. Умножение на произведение.

Чтобы умножить число на произведение нескольких чисел, можно умножить это число на первый сомножитель, полученный результат умножить на второй сомножитель и так далее до конца.

4 * [5 * (–2) * 3] = 4 * (–30) = –120
и
(4 * 5) * (–2) * 3 = 20 * (–2) * 3 = (–40) * 3 = –120.

Эти последние свойства вытекают из законов умножения

mthm.ru

Свойства умножения и деления

Свойства умножения

Переместительное свойство умножения

От перестановки множителей произведение не меняется.

Сочетательное свойство умножения

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

Переместительное и сочетательное свойства умножения позволяют сформулировать правило преобразования произведений.

При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.

Это свойство справедливо для любого количества слагаемых.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.

В буквенном виде свойство записывается так:

Свойства деления

• Ни одно число нельзя делить на ноль.
• При делении нуля на число получается ноль.

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

, где « k » — любое натуральное число.

Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.

Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.

math-prosto.ru

Умножение и деление целых чисел

При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.

При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть, какое правило применять. Также необходимо изучить несколько законов умножения и деления. Изучение этих правил позволяет избежать некоторые досадные ошибки в будущем.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов, и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например в выражении 3 × 2 = 6 , число 3 — это множимое, число 2 — множитель, число 6 — произведение.



Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть, в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в данном случае будет показывать сколько раз нужно взять число 3:



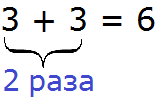
Таким образом, если взять число 3 два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

Теперь поменяем местами сомножители:

В обоих случаях, мы получаем ответ 15, значит между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

А с помощью переменных переместительный закон умножения можно записать так:

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:



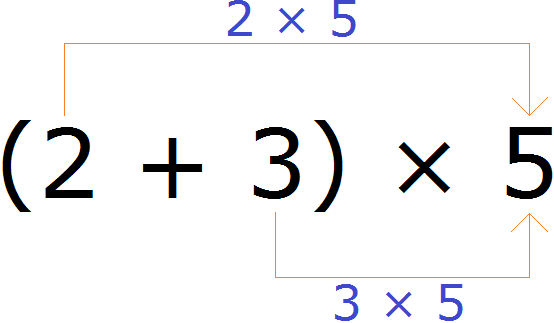
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25 .

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть, во сколько раз увеличить ноль. Буквально это выражение читается как «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль?

Другими словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

Примеры применения закона умножения на ноль:

2 × 5 × 0 × 9 × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Далее рассмотрим умножение целых чисел.

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают покороче: −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:



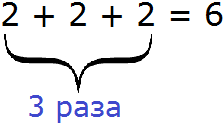
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы



А выражение (−5) + (−5) равно −10, и мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно записывают короче: 12 × (−5) = −60

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

Первое действие:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Обычно записывают короче: 10 × (−4) × 2 = −40 × 2 = −80

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Обычно записывают короче (−4) × (−2) = 8

Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.

Сначала запишем следующее выражение:

Заключим его в скобки:

Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:

Всё это приравняем к нулю:

( 4 × (−2) ) + ( (−4) × (−2) ) = 0

Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.

Итак, первое произведение ( 4 × (−2) ) равно −8. Запишем в нашем выражении число −8 вместо произведения ( 4 × (−2) )

Теперь вместо второго произведения временно поставим многоточие

Теперь внимательно смотрим на выражение −8 + […] = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.

Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8

Пример 5. Найти значение выражения −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = ( −2 × 6) + ( −2 × 4)

Теперь вычислим выражения, находящиеся в скобках. Затем полученные результаты сложим. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

−2 × 6 = −(2 × 6) = −(12) = −12

−2 × 4 = −(2 × 4) = −(8) = −8

Третье действие:

Значит значение выражения −2 × (6 + 4) равно −20

Обычно записывают короче: −2 × (6 + 4) = (−12) + (−8) = −20

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Второе действие:

Значит значение выражения (−2) × (−3) × (−4) равно −24

Обычно записывают короче: (−2) × (−3) × (−4) = 6 × (−4) = −24

Законы деления

Прежде чем делить целые числа, необходимо изучить два закона деления.

В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.



Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.

Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть, в ходе операции деления, число 8 будет разделено на две части.

Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.

Далее рассмотрим законы деления.

На ноль делить нельзя

Любое число запрещено делить на ноль. Дело в том, что деление является обратной операцией умножению. Например, если 2 × 6 = 12, то 12 : 6 = 2



Видно, что второе выражение записано в обратном порядке.

Теперь сделаем тоже самое для выражения 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю

Если записать это выражение в обратном порядке, то получим:

Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно и глупо.

В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0

В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть, каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.

Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.

Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8

Здесь вместо многоточия должно стоять число, которое при умножении на 2 даёт ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:

Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5

Здесь вместо многоточия должно стоять число, которое при умножении на 0 даёт ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.

Выражение […] × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.

А значит записывать выражение […] × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.

С помощью переменных данный закон записывается следующим образом:

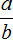, при b ≠ 0

Это выражение можно прочитать так:

Число a можно разделить на число b, при условии, что b не равно нулю.

Свойство частного

Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.

Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3



Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3



(12 × 4 ) : (4 × 4 )

(12 × 4 ) : (4 × 4 ) = 48 : 16 = 3

Получили ответ 3.

Теперь попробуем не умножить, а разделить делимое и делитель на число 4



(12 : 4 ) : (4 : 4 )

(12 : 4 ) : (4 : 4 ) = 3 : 1 = 3

Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.

Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.

Деление целых чисел

Пример 1. Найти значение выражения 12 : (−2)

Это деление чисел с разными знаками. 12 – это положительное число, (−2) – отрицательное. В таких случаях, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак минус.

12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6

Обычно записывают короче 12 : (−2) = −6

Пример 2. Найти значение выражения −24 : 6

Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. В таких случаях опять же нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак минус.

−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4

Обычно записывают короче −24 : 6 = −4

Пример 3. Найти значение выражения (−45) : (−5)

Это деление отрицательных чисел. В таких случаях, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.

(−45) : (−5) = |−45| : |−5| = 45 : 5 = 9

Обычно записывают короче (−45) : (−5) = 9

Пример 4. Найти значение выражения (−36) : (−4) : (−3)

Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.

Разделим (−36) на (−4), и полученное число разделим на (−3)

(−36) : (−4) = |−36| : |−4| = 36 : 4 = 9

9 : (−3) = −(|−9| : |−3|) = −(9 : 3) = −(3) = −3

Обычно записывают короче (−36) : (−4) : (−3) = 9 : (−3) = −3

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

spacemath.xyz

Урок «Умножение. Законы умножения».

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»



Напоминаем, что в соответствии с профстандартом педагога (утверждён Приказом Минтруда России), если у Вас нет соответствующего преподаваемому предмету образования, то Вам необходимо пройти профессиональную переподготовку по профилю педагогической деятельности. Сделать это Вы можете дистанционно на сайте проекта «Инфоурок» и получить диплом с присвоением квалификации уже через 2 месяца!

Только сейчас действует СКИДКА 50% для всех педагогов на все 111 курсов профессиональной переподготовки! Доступна рассрочка с первым взносом всего 10%, при этом цена курса не увеличивается из-за использования рассрочки!

Тема. Умножение . Законы умножения.

Изучение правила умножения натуральных чисел, переместительного закона умножения; формирование элементарных умений выполнять умножения натуральных чисел;

развитие основных умений выполнять умножение натуральных чисел по основному алгоритму; развитие внимания, логического мышления;

воспитание интереса к изучению предмета, умений работать в группах.

Планируемые образовательные результаты:

Предметные : ученик научится заменять действие умножения сложением и наоборот; находить необходимые компоненты умножения.

Личностные: , ученик получит возможность для формирования устойчивой учебной познавательной мотивации к учению, ясно и грамотно излагать свои мысли в устной речи, развивать интерес к различным видам деятельности.

Метапредметные : научиться действовать в соответствии с предложенным алгоритмом, осуществлять контроль своей деятельности. Получит возможность формулировать проблему при решении учебных задач. Аргументировать свое мнение и разрешать конфликтную ситуацию.

Регулятивные : уметь самостоятельно выполнять действия и вносить необходимые коррективы, регулировать свои действия для достижения высокой цели, в процессе рефлексии проводить оценку и самооценку.

Коммуникативные : участие в диалоге, участие в парной и групповой работе с использованием речевых средств для передачи своего мнения, подбор аргументов, формулирование выводов, отражение в устной и письменной форме результатов своей деятельности.

Проверка домашнего задания.

Актуализация опорных знаний.

Как называются компоненты при сложении?

Как найти неизвестное слагаемое?

Какие законы сложения вы знаете?

Как называются компоненты при вычитании?

Как найти неизвестное уменьшаемое? Вычитаемое?

У вас на столах лежат карточки с примерами. Устно решите примеры и составьте слово в таблице. Если вы правильно решите и заполните таблицу ответов, то сможете прочитать тему нашего урока ( Умножение . )

1. Найдите неизвестное число, обозначенное буквой х:
а) х + 27 = 61, б) 76 – х = 34, в) х – 18 = 21,

х = 61 – 27, х = 76 – 34, х = 21 + 18,

х = 34. х = 42. х = 36.

Ответ : 34. Ответ : 42. Ответ : 36.

2. Выполните действия «цепочкой»:

21 + 13 – 15 + 7 = 34 – 15 + 7 = 19 + 7 = 26.

24 – 16 + 15 – 21 = 8 + 15 – 21 = 23 – 21 = 2.

Объяснение нового материала.

Умножить натуральное число 3 на натуральное число 4 – значит найти сумму трех слагаемых, каждое из которых 4.

3  4 = 4 + 4 + 4 + 4 = 12.

Числа 3 и 4 называют множителями , 12 – произведение .

Запомните: Умножить число а на натуральное число b — значит найти сумму а одинаковых слагаемых, каждое из которых равно b .



Умножение — это арифметическое действие второй ступени.

Как называются компоненты при умножении? (Числа, которые нужно умножить, называ­ются множителями. Число, получаемое в результате умножения, называется произведением. ).

Понятно, что если один из множителей равен 1, то произведение равно второму множителю: а  1 = а, 1  а = а.

Если один из множителей равен 0, то произведение равно 0:

Пример 1 . Запишите произведение в виде суммы и найдите значение:

1) 5  3 = 3 + 3 + 3 + 3 + 3 = 15 (Записали сумму пяти слагаемых, каждое из которых равно 3);

2) 3  5 = 5 + 5 + 5 = 15 (Записали сумму трех слагаемых, каждое из которых равно 5);

3) 3  1 = 1 + 1 + 1 = 3 (Записали сумму трех слагаемых, каждое из которых равно 1);

4) 1  7 = 7 (Записали сумму одного слагаемого, которое равно 7).

Изменится ли произведение, если поменять местами множители? Нет.

Такое свойство справедливо для любых чисел а и b . Это — переместительный закон умножения.

Запомните: Переместительный закон умножения.

От перестановки множителей произведение не изменяется. а  b = b  а.

Вы уже знаете, что результат умножения нескольких множителей не зависит от порядка выполнения умно­жения. Например, чтобы найти произведение чисел 10, 2 и 15, можно сначала перемножить числа 10 и 2, а за­тем их произведение умножить на число 15. Но удобнее сначала перемножить числа 2 и 15, а затем на их произ­ведение умножить число 10. Порядок умножения чисел указывают при помощи скобок. Для рассматриваемого примера получим: (10  2)  15 = 10  (2  15).

Такое свойство справедливо для любых чисел а, b и с. Это — сочетательный закон умножения .

Запомните: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего. ( а  b )  с = а  ( b  с) .

Опираясь на переместительный и сочетательный за­коны, можно применять и такой способ группировки множителей: второе число умножить на произведение первого и третьего. Например, для нахождения про­изведения чисел 10, 2 и 15, кроме уже рассмотренных способов, существует третий способ: (10  15)  2.

Переместительный и сочетательный законы умноже­ния справедливы для любого количества множителей. Применяя эти законы, можно значительно упростить вычисления. Рассмотрим примеры.

Пример 2 . Найдите произведение:

1) 4  37  25 = (4  25)  37 = 100  37 = 3 700;

2) (25  5)  (4  20) = (25  4)  (5  20) = 100  100 = 10 000.

вычисляя произведение нескольких чисел, мож­но по-разному переставлять и группировать мно­жители;

если выражение в скобках содержит только действие умножения, то в таком выражении скобки можно опустить (не записывать).

-Давайте немножко взбодрим наше тело. Встаньте, пожалуйста, около своих парт и повторяйте за мной:

Руки подняли и помахали

Это деревья шумят.

В стороны руки и помахали

Это к нам птицы летят.

Быстро присели, руки сложили

В норке зверюшки сидят.

Встали и тихо за парты все сели.

Дети учиться хотят.

Уч.с.24 № 87(1ст.). Замените сумму произведением:

а) 75 + 75 = 2  75 (Образец рассмотрен в учебнике);

б) 701 + 701 = 2  701;

г) 603 + 603 + 603 = 3  603;

е) 16 + 16 + 16 + 16 + 16 + 16 = 6  16;

з) 172 + 172 + 172 + 172 + 172 = 5  172.

Уч.с.25 № 88(1ст.). Вычислите:

а) 4 + 4 + 4 = 3  4 = 12 (Образец рассмотрен в учебнике);

б) 7 + 7 + 7 = 3  7 = 21;

г) 11 + 11 + 11 + 11 + 11 = 5  11 = 55;

е) 46 + 46 + 46 + 46 + 46 + 46 = 6  46 = 276;

з) 128 + 128 + 128 + 128 + 128 = 5  128 = 640.

Уч.с.25 № 89(1ст.). Вычислите:

а) а + а + а = 3  а (Образец рассмотрен в учебнике);

б) b + b + b + b = 4  b ;

д) а + а + а + a = 4  а;

з) d + d + d + d + d = 5  d .

— Что нового узнали на уроке?

— Оцените свои знания по таблице:

Знаю: (что такое умножение)

Что значит умножить одно натуральное число на другое?

Как называются числа, которые перемножают?

Как называют результат умножения ?

Сформулируйте переместительное свойство умножения. Запишите его с помощью букв.

Чему равно произведение m ∙ 1 ?

Чему равно произведение n ∙ 0?

Домашнее задание. § 1.7 (выучить теорию). № 87(2ст), 88(2ст), 89(2ст), 72(в).

Учащиеся вычисляют примеры, работая в парах. Два ученика работают у доски.(Токарь Екатерина и Семенов Дмитрий)

Все учащиеся проверяют решение заданий, которые выполнялись у доски, сравнивая решение со своим в тетрадях.(Активно работают Чесноков Илья, Гетманова Ольга, Колпакова Дарья, Кушнир Игорь. Не справляются с заданием Салиев Эрвин и Александров

infourok.ru