Операции над событиями. Правила сложения и умножения вероятностей

Вероятностью события А называют отношение числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов: Р(А)=m/n.

Условной вероятностью события А (или вероятностью события А при условии, что наступило событие В), называется число РВ(А) = Р(АВ)/Р(В), где А и В – два случайных события одного и того же испытания.

Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них. Сумма двух событий обозначается А+В.

Правила сложения вероятностей:

  • правило сложения вероятностей совместных событий А и В:
    Р(А+В) = Р(А)+Р(В)-Р(АВ), где Р(А) – вероятность события А, Р(В) – вероятность события В, Р(А+В) – вероятность появления хотя бы одного из двух событий, Р(АВ)- вероятность совместного появления двух событий.
  • правило сложения вероятностей несовместных событий А и В:
    Р(А+В) = Р(А)+Р(В), где Р(А) – вероятность события А, Р(В) – вероятность события В.

    • Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет. Произведение двух событий обозначается АВ.

    Правила умножения вероятностей:

    • правило умножения вероятностей зависимых событий А и В:
      Р(АВ)= Р(А)*РА(В)= Р(В)*РВ(А), где РА(В) – условная вероятность наступления события В, если событие А уже наступило, РВ(А) – условная вероятность наступления события А, если событие В уже наступило;
    • правило умножения вероятностей независимых событий А и В:
      Р(АВ) = Р(А)*Р(В), где Р(А) – вероятность события А, Р(В) – вероятность события В.

      • Примеры решения задач по теме «Операции над событиями. Правила сложения и умножения вероятностей»

      Задача 1. В коробке имеется 250 лампочек, из них 100 по 90Вт, 50 — по 60Вт, 50 — по 25Вт и 50 – по 15Вт. Определить вероятность того, что мощность любой наугад взятой лампочки не превысит 60Вт.

      2. События А, В, С, D образуют полную систему, так как все они несовместны и одно из них обязательно наступит в данном опыте (выборе лампочки). Вероятность наступления одного из них есть достоверное событие, тогда Р(А)+Р(В)+Р(С)+Р(D)=1.

      3. События <�мощность лампочки не более 60Вт>(т.е. меньше или равна 60Вт), и <�мощность лампочки более 60Вт>(в данном случае – 90Вт) являются противоположными. По свойству противоположных чисел Р(В)+Р(С)+Р(D)=1-Р(А).

      4. Учитывая, что Р(В)+Р(С)+Р(D)=Р(В+С+D), получим Р(В+С+D)= 1-Р(А)=1-0,4=0,6.

      Задача 2. Вероятность поражения цели первым стрелком при одном выстреле равна 0,7, а вторым стрелком – 0,9. Найти вероятность того, что
      а) цель будет поражена только одним стрелком;
      б) цель будет поражена хотя бы одним стрелком.

      Решение.
      1. Рассматриваем следующие события:
      А1 = <�первый стрелок поражает цель>, Р(А1)=0,7 из условия задачи;
      А̄1 = <�первый стрелок промахнулся>, при этом Р(А1)+Р(А̄1) = 1, поскольку А1 и А̄1 – противоположные события. Отсюда Р(А̄1)=1-0,7=0,3;
      А2 = <�второй стрелок поражает цель>, Р(А2)=0,9 из условия задачи;
      А̄2 = <�второй стрелок промахнулся>, при этом Р(А̄2)=1-0,9=0,1.

      2. Событие А= <�цель поражена только одним стрелком>означает, что наступило одно из двух несовместных событий: либо А1А̄2, либо А̄1А2.
      По правилу сложения вероятностей Р(А)= Р(А1А̄2)+Р(А̄1А2).

      По правилу умножения вероятностей независимых событий:
      Р(А1А̄2)= Р(А1)*Р(А̄2)= 0,7*0,1=0,07;
      Р(А̄1А2)= Р(А̄1)*Р(А2)=0,3*0,9=0,27.
      Тогда Р(А)= Р(А1А̄2)+Р(А̄1А2)=0,07+0,27=0,34.

      3. Событие B= <�цель поражена хотя бы одним стрелком>означает, что либо цель поразил первый стрелок, либо цель поразил второй стрелок, либо цель поразили оба стрелка.

      Событие B̄= <�цель не поражена ни одним стрелком>является противоположным событию В, а значит Р(В)=1-Р(B̄).
      Событие B̄ означает одновременное появление независимых событий Ā1 и Ā2, следовательно Р(B̄)=Р(Ā1Ā2)= Р(Ā1)*Р(Ā2)=0,3*0,1=0,3.
      Тогда Р(В)= 1-Р(B̄)=1-0,3=0,7.

      Задача 3. Экзаменационный билет состоит из трех вопросов. Вероятность того, что студент ответит на первый вопрос 0,7; на второй – 0,9; на третий – 0,6. Найти вероятность того, что студент, выбрав билет ответит:
      а) на все вопросы;
      г) по крайней мере на два вопроса.

      Решение. 1. Рассматриваем следующие события:
      А1 = <�студент ответил на первый вопрос>, Р(А1)=0,7 из условия задачи;
      А̄1 = <�студент не ответил на первый вопрос>, при этом Р(А1)+Р(А̄1) = 1, поскольку А1 и А̄1 – противоположные события. Отсюда Р(А̄1)=1-0,7=0,3;
      А2 = <�студент ответил на второй вопрос>, Р(А2)=0,9 из условия задачи;
      А̄2 = <�студент не ответил на второй вопрос>, при этом Р(А̄2)=1-0,9=0,1;
      А3 = <�студент ответил на третий вопрос>, Р(А3)=0,6 из условия задачи;
      А̄3 = <�студент не ответил на третий вопрос>, при этом Р(А̄3)=1-0,6=0,4.

      2. Событие А = <�студент ответил на все вопросы>означает одновременное появление независимых событий А1, А2 и А3, т.е. Р(А)= Р(А1А2А3).По правилу умножения вероятностей независимых событий: Р(А1А2А3)= Р(А1)*Р(А2)*Р(А3)= 0,7*0,9*0,6=0,378.
      Тогда Р(А)= Р(А1А2А3)=0,378.

      3. Событие D = <�студент ответил по крайней мере на два вопроса>означает, что дан ответ на любые два вопроса или на все три, т.е. наступило одно из четырех несовместных событий: либо A1A2Ā3, либо А1Ā2А3, либо А̄1А2А3, либо А1А2А3.
      По правилу сложения вероятностей несовместных событий: Р(D)= Р(A1A2Ā3)+ Р(А1Ā2А3)+Р(А̄1А2А3)+Р(А1А2А3).

      По правилу умножения вероятностей независимых событий:
      Р(A1A2Ā3)= Р(A1)*Р(A2)*Р(Ā3)= 0,7*0,9*0,4=0,252;
      Р(А1Ā2А3)= Р(А1)*Р(Ā2)*Р(А3)= 0,7*0,1*0,6=0,042;
      Р(А̄1А2А3)= Р(А̄1)*Р(А2)*Р(А3)= 0,3*0,9*0,6=0,162;
      Р(А1А2А3)= Р(А1)*Р(А2)*Р(А3)= 0,7*0,9*0,6=0,378.
      Тогда Р(D)= 0,252+0,042+0,162+0,378= 0,834.

      Другие статьи по данной теме:

      • назад:Элементы комбинаторики. События и их вероятности. Примеры решения задач (Часть 2)
      • далее:Формула полной вероятности. Формулы Бейеса. Примеры решения задач

      Список использованных источников

  1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
  2. Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
  3. Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
  4. Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.

www.ekonomika-st.ru

Типичные ошибки при решении задач по теории вероятностей.

на применение правил сложения и умножения вероятностей событий.

Событие состоящее в наступлении хотя бы одного из событий А и В, называется суммой или объединением этих событий и обозначается А+В или A∨B.

Событие состоящее в наступлении обоих событий А и В называется произведением или совмещением событий А и В и обозначается А·В или A∧B.

Эту теорему также можно обобщить на случай произвольного числа независимых событий.

Пример 1

Вероятность того, что чайник прослужит больше года, равна 0,93. Вероятность того, что чайник прослужит больше 2 лет, равна 0,87. Найдите вероятность того, что чайник прослужит больше года, но меньше 2 лет.

Этот пример взят из банка заданий ЕГЭ 2016 по математике профильного уровня. А решение, которое приводится ниже, с одного из сайтов в сети Интернет. (Сайт не называю, потому что право на ошибку имеют все, но решение прилагаю на снимке с экрана, чтобы не было сомнений в его реальности.)

Как вы думаете, верное или неверное это решение? Почему?
Постарайтесь ответить на этот вопрос самостоятельно раньше, чем откроете следующие комментарии.

Введём обозначения:
А — «Чайник прослужит больше года», p(А) = 0,93;
B — «Чайник прослужит больше 2 лет», p(B) = 0,87;
С — «Чайник прослужит больше года, но меньше 2 лет», p(С) = ?

Событие С можно сформулировать иначе: «Чайник прослужит больше года, но не прослужит больше 2-ух лет». Это верно.
Событие В _ — «не прослужит больше 2-ух лет» противоположно событию В, поэтому его вероятность p( В _ ) = 1 − p(B). Верно.
Далее автор решения явно или неяно в новой формулировке события С заменил союз «но» союзом «и» — «Чайник прослужит больше года И не прослужит больше 2-ух лет» — и пришел к выводу, что имеет дело с произведением событий А и В _ . Приемлемо.
И, наконец, пользуясь теоремой умножения вероятностей, которую также называют И-правилом, автор перешёл от произведения событий к умножению их вероятностей и получил p(C) = p(A)·(1 − p(B)) = 0,93·(1 − 0,87) = 0,93·0,13 = 0,1209. Однако .

Событие «чайник прослужит больше 2 лет» содержит в себе событие «чайник прослужит больше года». Событие В не может произойти, если не произошло событие А.
Событие «не прослужит больше 2-ух лет» содержит в себе событие «не прослужит больше года». Событие A _ влечёт за собой событие В _ .
Другими словами, чайник не может прослужить больше двух лет, если он сломался в течение первого года. Если чайник успешно проработал 3 года, то реализовались оба события A и B. Если чайник сломался через 6 месяцев после покупки, реализовались оба противоположных события A _ и В _ .
Таким образом, все эти события зависимы! друг от друга и к ним НЕЛЬЗЯ применять теорему умножения вероятностей. Прочитайте её формулировку еще раз. Там чётко сказано «Вероятность произведения двух независимых событий . «.
Для определения вероятности произведения зависимых событий есть расширенный вариант этой теоремы, содержащий понятие условная вероятность, но в этой задаче нет таких данных. Она решается просто совсем другим способом.

Решение.
Один и тот же чайник не может сломаться одновременно и в первый, и во второй годы службы. Эти события не совместимы.
Событие А — «Чайник прослужит больше года» — распадается на два случая: чайник сломается на втором году службы ИЛИ продолжит работать дальше, т.е. прослужит больше 2 лет.
Следовательно, событие А является суммой двух несовместимых событий С и В, к которым применима теорема сложения вероятностей (ИЛИ-правило).
A = C + B
p(A) = p(C) + p(B).
0,93 = p(C) + 0,87.
p(C) = 0,93 − 0,87 = 0,06.

Ответ: 0,06.

Проверка.
Для проверки (или в качестве второго способа решения) можно использовать следующий факт — «при большом числе наблюдений относительная частота исходов испытаний совпадает с вероятностью этих исходов.»
Пусть было приобретено 1000 чайников.
Больше года прослужило 1000×0,93 = 930 чайников.
Больше 2-ух лет прослужило 1000×0,87 = 870 чайников.
За второй год наблюдений сломалось 60 чайников из приобретённой тысячи. р = 60/1000 = 0,06.

Пример 2

Из районного центра в деревню ежедневно ходит автобус . Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров равна 0,82. Вероятность того, что окажется меньше 10 пассажиров равна 0,51. Найдите вероятность того что, число пассажиров будет от 10 до 17.

Этот пример также из банка заданий ЕГЭ 2016 по математике профильного уровня. Решение с того же сайта, но, судя по скриншоту, принадлежит другому автору.

Верное или неверное решение? Почему?
Если здесь есть ошибка и Вы сможете найти её самостоятельно, то получите дополнительную уверенность в своих знаниях. Не упустите случай порадоваться за себя. Не спешите открывать мои комментарии.

Смотреть комментарии.

Смотреть решение.

Решение.
Примем те же обозначения событий.
Событие «в автобусе окажется меньше 18 пассажиров» (событие Б) реализуется одним из двух вариантов ИЛИ их будет меньше 10 (событие В), ИЛИ от 10 до 17 (событие А). Причём эти случаи несовместимы. Поэтому применяем ИЛИ-правило (теорему сложения вероятностей) в самой простой форме.
Б = В + А;
Р(Б) = Р(В) + P(А);
0,82 = 0,51 + Р(А);
P(A) = 0,82 − 0,51 = 0,31.

Ответ: 0,31.

Итак, в теоремах сложения и умножения вероятностей главное вовсе не математические формулы, которые легко запомнить и применять. Важнее анализ самих событий, их независимости и совместимости. Для правильного решения таких задач требуется не только знание математики, как её понимают школьники, но и зрелость мышления в целом.

Если Вы попали на эту страницу из поисковика, то рекомендую ознакомиться с другими задачами на эту тему. И неважно предстоит ли Вам в этом году сдавать ЕГЭ по математике, или Вы уже студент, — это просто хорошие задачи на сложение и умножение вероятностей.

Переход на главную страницу, сайта «Математичка».

mathematichka.ru

Теоремы сложения и умножения вероятностей

Теорема сложения вероятностей несовместных событий

Теорема. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий

(2.1)

Доказательство. Докажем эту теорему для случая суммы двух несовместных событий и .

Пусть событию благоприятствуют элементарных исходов, а событию исходов. Так как события и по условию теоремы несовместны, то событию благоприятствуют элементарных исходов из общего числа n исходов. Следовательно,

,

где — вероятность события ; — вероятность события .

Пример. Для отправки груза со склада может быть выделена одна из двух машин различного вида. Известны вероятности выделения каждой машины: . Тогда вероятность поступления к складу хотя бы одной из этих машин будет

Условная вероятность

Во многих случаях вероятности появления одних событий зависят от того, произошло или нет другое событие. Например, вероятность своевременного выпуска машины зависит от поставки комплектующих изделий. Если эти изделия уже поставлены, то искомая вероятность будет одна. Если же она определяется до поставки комплектующих, то ее значение, очевидно, будет другим.

Вероятность события , вычисленная при условии, что имело место другое событие , называется условной вероятностью события и обозначается .

В тех случаях, когда вероятность события рассматривается при условии, что произошло два других события , используется условная вероятность относительно произведения событий

Теорема умножения вероятностей

Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место

P(AB) = P(A)×P(B/A) = P(B)×P(A/B). (2.2)

Доказательство. Предположим, что из всевозможных элементарных исходов событию благоприятствуют исходов, из которых исходов благоприятствуют событию . Тогда вероятность события будет , условная вероятность события относительно события будет .

Произведению событий и благоприятствуют только те исходы, которые благоприятствуют и событию и событию одновременно, т.е. исходов. Поэтому вероятность произведения событий и равна

Умножим числитель и знаменатель этой дроби на . Получим

Аналогично доказывается и формула

Пример. На склад поступило 35 холодильников. Известно, что 5 холодильников с дефектами, но неизвестно, какие это холодильники. Найти вероятность того, что два взятых наугад холодильника будут с дефектами.

Решение. Вероятность того, что первый выбранный холодильник будет с дефектом, находится как отношение числа благоприятствующих исходов к общему числу возможных исходов

P(A) = 5/35 = 1/7.

Но после того, как был взят первый холодильник с дефектом, условная вероятность того, что и второй будет с дефектом, определяется на основе соотношения

Искомая вероятность будет

Если при наступлении события вероятность события не меняется, то события и называются независимыми.

В случае независимых событий вероятность их произведения равна произведению вероятностей этих событий

P(AB) = P(A)×P(B). (2.3)

Теорема умножения вероятностей легко обобщается на любое конечное число событий.

Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий, т.е.

P(ABC. LM) = P(A)×P(B/A)×P(C/AB) P(M/AB. L). (2.4)

Для доказательства этой теоремы можно использовать метод математической индукции.

Теорема сложения вероятностей совместных событий

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же опыте.

Пример. Поступление в магазин одного вида товара — событие . Поступление второго вида товара — событие . Поступить эти товары могут и одновременно. Поэтому и — совместные события.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

P(A+B) = P(A) + P(B) — P(AB). (2.5)

Доказательство. Событие наступит, если наступит одно из трех несовместных событий , , . По теореме сложения вероятностей несовместных событий имеем

(2.6)

Событие произойдет, если наступит одно из двух несовместных событий: , . Вновь применяя теорему сложения вероятностей несовместных событий, получаем . Откуда

(2.7)

Аналогично для события Откуда

.(2.8)

Подставив (2.7) и (2.8) в (2.6), находим

P(A+B) = P(A) + P(B) — P(AB).

Пример. Если вероятность поступления в магазин одного вида товара равна P(A) = 0,4, а второго товара — P(B) = 0,5, и если допустить, что эти события независимы, но совместны, то вероятность суммы событий равна

P(A+B) = 0,4 + 0,5 — 0,4×0,5 = 0,7.

www.grandars.ru

Теоремы сложения и умножения вероятностей.
Зависимые и независимые события

Заголовок выглядит страшновато, но в действительности всё очень просто. На данном уроке мы познакомимся с теоремами сложения и умножения вероятностей событий, а также разберём типовые задачи, которые наряду с задачей на классическое определение вероятности обязательно встретятся или, что вероятнее, уже встретились на вашем пути. Для эффективного изучения материалов этой статьи необходимо знать и понимать базовые термины теории вероятностей и уметь выполнять простейшие арифметические действия. Как видите, требуется совсем немного, и поэтому жирный плюс в активе практически гарантирован. Но с другой стороны, вновь предостерегаю от поверхностного отношения к практическим примерам – тонкостей тоже хватает. В добрый путь:

Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событи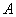й или 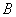(без разницы какого), равна сумме вероятностей этих событий:

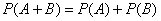
Аналогичный факт справедлив и для бОльшего количества несовместных событий, например, для трёх несовместных событи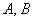й и :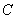

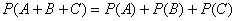
Теорема-мечта =) Однако, и такая мечта подлежит доказательству, которое можно найти, например, в учебном пособии В.Е. Гмурмана.

Давайте сразу вспомним алгебру событий: сложение событий означает появление хотя бы одного из суммируемых событий, и, поскольку события в данном случае НЕсовместны, то одного и только одного из этих событий (безразлично какого).

Следует отметить, что для совместных событий равенство 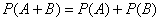будет неверным, не случайно чуть выше я немного сыронизировал на счёт простоты. Теорема сложения вероятностей совместных событий имеет гораздо меньшее значение практики
(и более того, может запутать «чайника»), поэтому о ней чуть позже.

А сейчас возьмём в руки уже знакомое и безотказное орудие труда учёбы – игральный кубик с полной группой событий 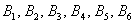, которые состоят в том, что при его броске выпадут 1, 2, 3, 4, 5 и 6 очков соответственно.

Рассмотрим событие 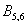– в результате броска игральной кости выпадет не менее пяти очков. Данное событие состоит в двух несовместных исходах: 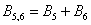(выпадет 5 или 6 очков). По теореме сложения вероятностей несовместных событий:
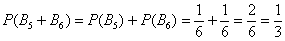– вероятность того, что в результате броска игральной кости выпадет не менее пяти очков.

Рассмотрим событие 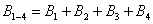, состоящее в том, что выпадет не более 4 очков и найдем его вероятность. По теореме сложения вероятностей несовместных событий:

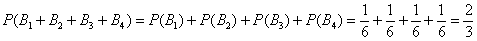
По той же теореме, вероятность того, что выпадет нечётное число очков:
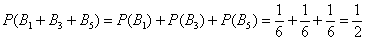и так далее.

С помощью рассматриваемой теоремы можно решить некоторые задачи, которые нам встретились на практикуме по классическому определению вероятности. Не поленюсь, кратко перескажу решение 13-го примера вышеуказанного урока:

«Студент знает ответы на 25 экзаменационных вопросов из 60. Какова вероятность сдать экзамен, если для этого необходимо ответить не менее чем на 2 из 3 вопросов?»

В той задаче мы сначала нашли 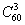(количество всех возможных сочетаний трёх вопросов), затем вычислили 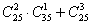количество благоприятствующих исходов и вероятность 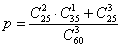того, что студент сдаст экзамен.

Но здесь вместо правила сложений комбинаций в ходу и другая схема рассуждений. Рассмотрим два несовместных события:

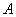– студент ответит на два вопроса из трёх;
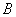– студент ответит на все три вопроса.

Возможно, некоторые читатели ещё не до конца осознали суть несовместности. Вдумаемся ещё раз: студент не может ответить на 2 вопроса из 3 и в то же самое время ответить на все 3 вопроса. Таким образом, события 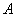и 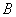– несовместны.

Теперь, пользуясь классическим определением, найдём их вероятности:

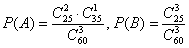
Факт успешной сдачи экзамена выражается суммой 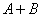(ответ на 2 вопроса из 3 или на все вопросы). По теореме сложения вероятностей несовместных событий:
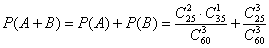– вероятность того, что студент сдаст экзамен.

Этот способ решения совершенно равноценен, выбирайте, какой больше нравится.

Разминаемся в подсобке:

Магазин получил продукцию в ящиках с четырех оптовых складов: четыре с 1-го, пять со 2-го, семь с 3-го и четыре с 4-го. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада.

Решение: всего получено магазином: 4 + 5 + 7 + 4 = 20 ящиков.

В данной задаче удобнее воспользоваться «быстрым» способом оформления без расписывания событий большими латинскими буквами. По классическому определению:
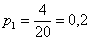– вероятность того, что для продажи будет выбран ящик с 1-го склада;
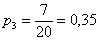– вероятность того, что для продажи будет выбран ящик с 3-го склада.

Бесконечных «хвостов» после запятой тут нет и не ожидается, поэтому можно работать с десятичными дробями – компактнее будет запись.

По теореме сложения несовместных событий:
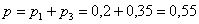– вероятность того, что для продажи будет выбран ящик с первого или третьего склада.

Ответ: 0,55

Безусловно, задача разрешима и чисто через классическое определение вероятности путём непосредственного подсчёта кол-ва благоприятствующих исходов (4 + 7 = 11), но рассмотренный способ ничем не хуже. И даже чётче.

Ещё один товар на соседнем стеллаже:

В коробке 10 красных и 6 синих пуговиц. Наудачу извлекаются две пуговицы. Какова вероятность того, что они будут одноцветными?

Аналогично – здесь можно использовать комбинаторное правило суммы, но мало ли … вдруг кто-то его запамятовал, а то и вовсе проехал мимо с песнями. Тогда на помощь придёт теорема сложения вероятностей несовместных событий! Решение и ответ в конце статьи (оформлено в «ускоренном» стиле)

Внимание! Если у вас возникло хоть какое-то недопонимание по вышеизложенному материалу, то настоятельно рекомендую обратиться к предыдущим урокам курса. Ибо не знать азов комбинаторики и не уметь решать типовые задачи на К.О.В. – совсем скверно( В тяжёлом случае следует начать с основ теории вероятностей.

Знакомимся с новыми, до сих пор не встречавшимися понятиями:

Зависимые и независимые события

Начнём с независимых событий. События являются независимыми, если вероятность наступления любого из них не зависит от появления/непоявления остальных событий рассматриваемого множества (во всех возможных комбинациях). …Да чего тут вымучивать общие фразы:

Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событи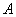й и 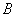равна произведению вероятностей этих событий:

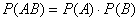
Вернёмся к простейшему примеру 1-го урока, в котором подбрасываются две монеты и следующим событиям:

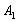– на 1-й монете выпадет орёл;
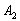– на 2-й монете выпадет орёл.

Найдём вероятность события 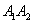(на 1-й монете появится орёл и на 2-й монете появится орёл – вспоминаем, как читается произведение событий!). Вероятность выпадения орла на одной монете никак не зависит от результата броска другой монеты, следовательно, события 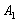и 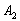независимы. По теореме умножения вероятностей независимых событий:

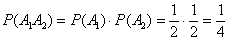
Аналогично:
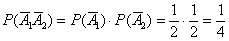– вероятность того, что на 1-й монете выпадет решка и на 2-й решка;
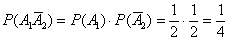– вероятность того, что на 1-й монете появится орёл и на 2-й решка;
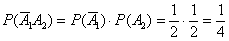– вероятность того, что на 1-й монете появится решка и на 2-й орёл.

Заметьте, что события 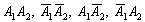образуют полную группу и сумма их вероятностей равна единице: .

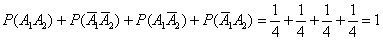Теорема умножения очевидным образом распространяется и на бОльшее количество независимых событий, так, например, если события 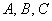независимы, то вероятность их совместного наступления равна: 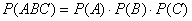. Потренируемся на конкретных примерах:

В каждом из трех ящиков имеется по 10 деталей. В первом ящике 8 стандартных деталей, во втором – 7, в третьем – 9. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.

Решение: вероятность извлечения стандартной или нестандартной детали из любого ящика не зависит от того, какие детали будут извлечены из других ящиков, поэтому в задаче речь идёт о независимых событиях. Рассмотрим следующие независимые события:

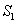– из 1-го ящика извлечена стандартная деталь;
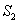– из 2-го ящика извлечена стандартная деталь;
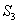– из 3-го ящика извлечена стандартная деталь.

По классическому определению:
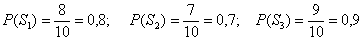– соответствующие вероятности.

Интересующее нас событие (из 1-го ящика будет извлечена стандартная деталь и из 2-го стандартная и из 3-го стандартная) выражается произведением .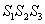

По теореме умножения вероятностей независимых событий:

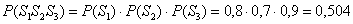– вероятность того, что из трёх ящиков будет извлечено по одной стандартной детали.

Ответ: 0,504

После бодрящих упражнений с ящиками нас поджидают не менее интересные урны:

В трех урнах имеется по 6 белых и по 4 черных шара. Из каждой урны извлекают наудачу по одному шару. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета.

Опираясь на полученную информацию, догадайтесь, как разобраться с пунктом «бэ» 😉 Примерный образец решения оформлен в академичном стиле с подробной росписью всех событий.

Зависимые события. Событие 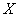называют зависимым, если его вероятность 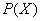зависит от одного или бОльшего количества событий, которые уже произошли. За примерами далеко ходить не надо – достаточно до ближайшего магазина:

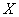– завтра в 19.00 в продаже будет свежий хлеб.

Вероятность этого события зависит от множества других событий: завезут ли завтра свежий хлеб, раскупят ли его до 7 вечера или нет и т.д. В зависимости от различных обстоятельств данное событие может быть как достоверным 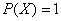, так и невозможным 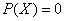. Таким образом, событие 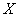является зависимым.

Хлеба… и, как требовали римляне, зрелищ:

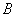– на экзамене студенту достанется простой билет.

Если идти не самым первым, то событие 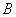будет зависимым, поскольку его вероятность 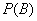будет зависеть от того, какие билеты уже вытянули однокурсники.

Как определить зависимость/независимость событий?

Иногда об этом прямо сказано в условии задачи, но чаще всего приходится проводить самостоятельный анализ. Какого-то однозначного ориентира тут нет, и факт зависимости либо независимости событий вытекает из естественных логических рассуждений.

Чтобы не валить всё в одну кучу, задачам на зависимые события я выделю следующий урок, а пока мы рассмотрим наиболее распространённую на практике связку теорем:

Задачи на теоремы сложения вероятностей несовместных
и умножения вероятностей независимых событий

Этот тандем, по моей субъективной оценке, работает примерно в 80% задач по рассматриваемой теме. Хит хитов и самая настоящая классика теории вероятностей:

Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Найти вероятность того, что:

а) только один стрелок попадёт в мишень;
б) хотя бы один из стрелков попадёт в мишень.

Решение: вероятность попадания/промаха одного стрелка, очевидно, не зависит от результативности другого стрелка.

Рассмотрим события:
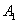– 1-й стрелок попадёт в мишень;
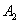– 2-й стрелок попадёт в мишень.

По условию: .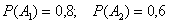

Найдём вероятности противоположных событий 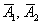– того, что соответствующие стрелки промахнутся:

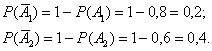
а) Рассмотрим событие: 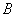– только один стрелок попадёт в мишень. Данное событие состоит в двух несовместных исходах:

1-й стрелок попадёт и 2-й промахнётся
или
1-й промахнётся и 2-й попадёт.

На языке алгебры событий этот факт запишется следующей формулой:

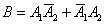
Сначала используем теорему сложения вероятностей несовместных событий, затем – теорему умножения вероятностей независимых событий:

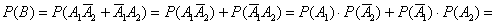
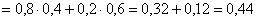– вероятность того, что будет только одно попадание.

б) Рассмотрим событие: 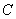– хотя бы один из стрелков попадёт в мишень.

Прежде всего, ВДУМАЕМСЯ – что значит условие «ХОТЯ БЫ ОДИН»? В данном случае это означает, что попадёт или 1-й стрелок (2-й промахнётся) или 2-й (1-й промахнётся) или оба стрелка сразу – итого 3 несовместных исхода.

Способ первый: учитывая готовую вероятность предыдущего пункта, событие 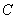удобно представить в виде суммы следующих несовместных событий:

попадёт кто-то один (событие 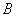, состоящее в свою очередь из 2 несовместных исходов) или
попадут оба стрелка – обозначим данное событие буквой .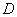

Таким образом: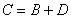

По теореме умножения вероятностей независимых событий:
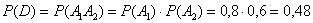– вероятность того, что 1-й стрелок попадёт и 2-й стрелок попадёт.

По теореме сложения вероятностей несовместных событий:
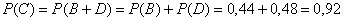– вероятность хотя бы одного попадания по мишени.

Способ второй: рассмотрим противоположное событие: 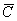– оба стрелка промахнутся.

По теореме умножения вероятностей независимых событий:

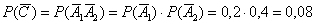
В результате: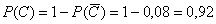

Особое внимание обратите на второй способ – в общем случае он более рационален.

Кроме того, существует альтернативный, третий путь решения, основанный на умолчанной выше теореме сложения совместных событий.

! Если вы знакомитесь с материалом впервые, то во избежание путаницы, следующий абзац лучше пропустить.

Способ третий: события 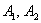совместны, а значит, их сумма 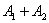выражает событие «хотя бы один стрелок попадёт в мишень» (см. алгебру событий). По теореме сложения вероятностей совместных событий и теореме умножения вероятностей независимых событий:

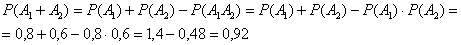
Выполним проверку: события 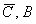и 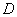(0, 1 и 2 попадания соответственно) образуют полную группу, поэтому сумма их вероятностей должна равняться единице:
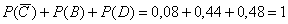, что и требовалось проверить.

Ответ: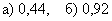

При основательном изучении теории вероятностей вам встретятся десятки задач милитаристского содержания, и, что характерно, после этого никого не захочется пристрелить – задачи почти подарочные. А почему бы не упростить ещё и шаблон? Cократим запись:

Решение: по условию: 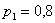, 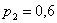– вероятность попадания соответствующих стрелков. Тогда вероятности их промаха:

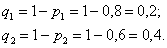
а) По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
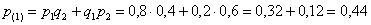– вероятность того, что только один стрелок попадёт в мишень.

б) По теореме умножения вероятностей независимых событий:
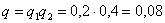– вероятность того, что оба стрелка промахнутся.

Тогда: 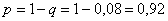– вероятность того, что хотя бы один из стрелков попадёт в мишень.

Ответ: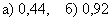

На практике можно пользоваться любым вариантом оформления. Конечно же, намного чаще идут коротким путём, но не нужно забывать и 1-й способ – он хоть и длиннее, но зато содержательнее – в нём понятнее, что, почему и зачем складывается и умножается. В ряде случаев уместен гибридный стиль, когда прописными буквами удобно обозначить лишь некоторые события.

Похожие задачи для самостоятельного решения:

Для сигнализации о возгорании установлены два независимо работающих дат­чика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре:

а) оба датчика откажут;
б) оба датчика сработают.
в) Пользуясь теоремой сложения вероятностей событий, образующих полную группу, найти вероятность того, что при пожаре сработает только один датчик. Проверить результат прямым вычислением этой вероятности (с помощью теорем сложения и умножения).

Здесь независимость работы устройств непосредственно прописана в условии, что, кстати, является важным уточнением. Образец решения оформлен в академичном стиле.

Как быть, если в похожей задаче даны одинаковые вероятности, например, 0,9 и 0,9? Решать нужно точно так же! (что, собственно, уже продемонстрировано в примере с двумя монетами)

Вероятность поражения цели первым стрелком при одном выстреле равна 0,8. Вероятность того, что цель не поражена после выполнения первым и вторым стрелками по одному выстрелу равна 0,08. Какова вероятность поражения цели вторым стрелком при одном выстреле?

А это небольшая головоломка, которая оформлена коротким способом. Условие можно переформулировать более лаконично, но переделывать оригинал не буду – на практике приходится вникать и в более витиеватые измышления.

Знакомьтесь – он самый, который настрогал для вас немереное количество деталей =):

Рабочий обслуживает три станка. Вероятность того, что в течение смены первый станок потребует настройки, равна 0,3, второй – 0,75, третий – 0,4. Найти вероятность того, что в течение смены:

а) все станки потребуют настройки;
б) только один станок потребует настройки;
в) хотя бы один станок потребует настройки.

Решение: коль скоро в условии ничего не сказано о едином технологическом процессе, то работу каждого станка следует считать не зависимой от работы других станков.

По аналогии с Задачей №5, здесь можно ввести в рассмотрение события 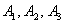, состоящие в том, что соответствующие станки потребуют настройки в течение смены, записать вероятности 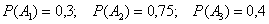, найти вероятности противоположных событий 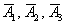и т.д. Но с тремя объектами так оформлять задачу уже не очень хочется – получится долго и нудно. Поэтому здесь заметно выгоднее использовать «быстрый» стиль:

По условию: 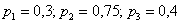– вероятности того, что в течение смены соответствующие станки потребуют настойки. Тогда вероятности того, что они не потребуют внимания:

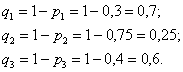
. Один из читателей обнаружил тут прикольную опечатку, даже исправлять не буду =)

а) По теореме умножения вероятностей независимых событий:
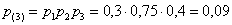– вероятность того, что в течение смены все три станка потребуют настройки.

б) Событие «В течение смены только один станок потребует настройки» состоит в трёх несовместных исходах:

1) 1-й станок потребует внимания и 2-й станок не потребует и 3-й станок не потребует
или:
2) 1-й станок не потребует внимания и 2-й станок потребует и 3-й станок не потребует
или:
3) 1-й станок не потребует внимания и 2-й станок не потребует и 3-й станок потребует.

По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

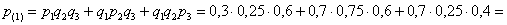
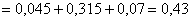– вероятность того, что в течение смены только один станок потребует настройки.

Думаю, сейчас вам должно быть понятно, откуда взялось выражение

в) Вычислим вероятность 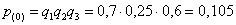того, что станки не потребуют настройки, и затем – вероятность противоположного события:
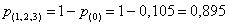– того, что хотя бы один станок потребует настройки.

Ответ: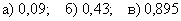

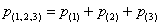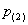Пункт «вэ» можно решить и через сумму , где – вероятность того, что в течение смены только два станка потребуют настройки. Это событие в свою очередь включает в себя 3 несовместных исхода, которые расписываются по аналогии с пунктом «бэ». Постарайтесь самостоятельно найти вероятность 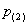, чтобы проверить всю задачу с помощью равенства .

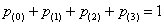Далее… …правильно догадываетесь – любимая тема =):

Из трех орудий произвели залп по цели. Вероятность попадания при одном выстреле только из первого орудия равна 0,7, из второго – 0,6, из третьего – 0,8. Найти вероятность того, что: 1) хотя бы один снаряд попадет в цель; 2) только два снаряда попадут в цель; 3) цель будет поражена не менее двух раз.

Решение и ответ в конце урока.

И снова о совпадениях: в том случае, если по условию два или даже все значения исходных вероятностей совпадают (например, 0,7; 0,7 и 0,7), то следует придерживаться точно такого же алгоритма решения.

В заключение статьи разберём ещё одну распространённую головоломку:

Стрелок попадает в цель с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность хотя бы одного попадания при трех выстрелах равна 0,973.

Решение: обозначим через 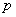– вероятность попадания в мишень при каждом выстреле.
и через 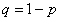– вероятность промаха при каждом выстреле.

И таки распишем события:
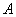– при 3 выстрелах стрелок попадёт в мишень хотя бы один раз;
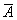– стрелок 3 раза промахнётся.

По условию 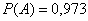, тогда вероятность противоположного события:

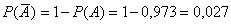
С другой стороны, по теореме умножения вероятностей независимых событий:

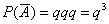
Таким образом:

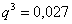
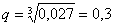– вероятность промаха при каждом выстреле.

В результате:
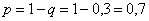– вероятность попадания при каждом выстреле.

Ответ: 0,7

Просто и изящно.

В рассмотренной задаче можно поставить дополнительные вопросы о вероятности только одного попадания, только двух попаданий и вероятности трёх попаданий по мишени. Схема решения будет точно такой же, как и в двух предыдущих примерах:

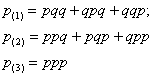
Однако принципиальное содержательное отличие состоит в том, что здесь имеют место повторные независимые испытания, которые выполняются последовательно, независимо друг от друга и с одинаковой вероятностью исходов.

Несмотря на кажущуюся шаблонность примеров, целесообразно ознакомиться с дополнительными задачами на теоремы сложения и умножения вероятностей, которые на самом деле достаточно разнообразны. Кроме того, в предложенном файле прорешаны более трудные задачи с «четырьмя участниками».

На следующем уроке мы разберём задачи с зависимыми событиями, а затем важнейшие следствия рассмотренных теорем – формулу полной вероятности, формулы Байеса и формулу Бернулли, касающуюся независимых испытаний.

Везения в главном!

Решения и ответы:

Задача 2: Решение: всего: 10 + 6 = 16 пуговиц в коробке.
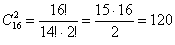способами можно извлечь 2 пуговицы из коробки;
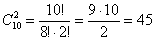способами можно извлечь 2 красные пуговицы;
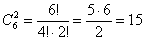способами можно извлечь 2 синие пуговицы.
По классическому определению:
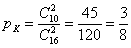– вероятность того, что из коробки будут извлечены две красные пуговицы;
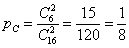– вероятность того, что из коробки будут извлечены две синие пуговицы.
По теореме сложения вероятностей несовместных событий:
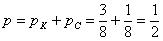– вероятность того, что из коробки будут извлечены две одноцветные пуговицы.
Ответ: 0,5

Задача 4: Решение: рассмотрим события: 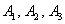– из 1-й, 2-й и 3-й урны соответственно будет извлечён белый шар. По классическому определению вероятности:

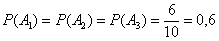
Тогда вероятности извлечения чёрного шара из соответствующих урн равны:

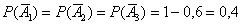
а) Рассмотрим событие: 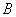– из каждой урны будет извлечено по 1 белому шару.
Данное событие выражается в виде произведения 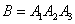(из 1-й урны будет извлечён БШ и из 2-й урны будет извлечён БШ и из 3-й урны будет извлечён БШ).
По теореме умножения вероятностей независимых событий:

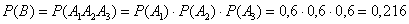
б) Рассмотрим событие 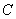– из каждой урны будет извлечено по 1 чёрному шару.
По теореме умножения вероятностей независимых событий:

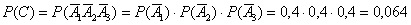
Рассмотрим событие 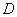– все три шара будут одного цвета. Данное событие состоит в двух несовместных исходах: 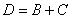(будут извлечены 3 белых или 3 чёрных шара)
По теореме сложения вероятностей несовместных событий:

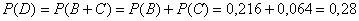
Ответ: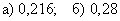

Задача 6: Решение: рассмотрим следующие события:
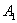– при возгорании сработает 1-й датчик;
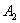– при возгорании сработает 2-й датчик.
По условию: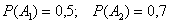
Вычислим вероятности противоположных событий:

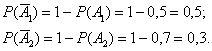
а) Рассмотрим событие: 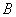– при пожаре оба датчика откажут.
По теореме умножения вероятностей независимых событий:

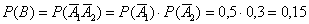
б) Рассмотрим событие: 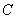– при пожаре оба датчика сработают.
По теореме умножения вероятностей независимых событий:

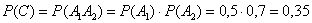
в) Рассмотрим событие: 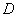– при пожаре сработает только один датчик.
События 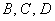образуют полную группу, следовательно:

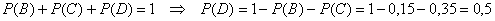
Проверим результат с помощью прямого вычисления. Событие 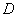состоит в 2 несовместных исходах: 1-й датчик сработает и 2-й откажет или 1-й откажет и 2-й сработает. Таким образом: .
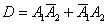По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

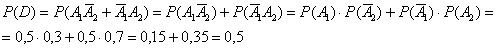
Ответ: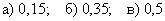

Задача 7: Решение: по условию: 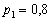– вероятность поражения цели первым стрелком при одном выстреле. Тогда вероятность его промаха:

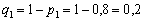
Обозначим через 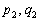– вероятности попадания и промаха 2-го стрелка.
По теореме умножения вероятностей независимых событий:
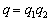– вероятность того, что оба стрелка промахнутся.
По условию 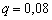, таким образом:

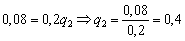
В результате: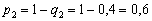
Ответ: 0,6

Задача 9: Решение: по условию 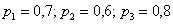– вероятности попадания в цель из соответствующих орудий. Тогда соответствующие вероятности промаха:

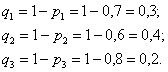
1) По теореме умножения вероятностей независимых событий:
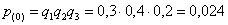– вероятность того, что будет три промаха.
Тогда: 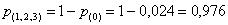– вероятность того, что хотя бы один снаряд попадет в цель.

2) Событие «только два снаряда попадут в цель» состоит в трёх несовместных исходах:
попадание из 1-го и 2-го орудий и промах из 3-го или
попадание из 1-го и промах из 2-го и попадание из 3-го орудия или
промах из 1-го и попадание из 2-го и 3-го орудий.
По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

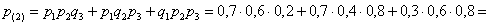
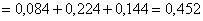– вероятность того, что только два снаряда попадут в цель.

3) По теореме умножения вероятностей независимых событий:
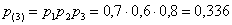– вероятность того, что все три снаряда попадут в цель.
По теореме сложения вероятностей несовместных событий:
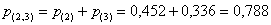– вероятность того, что цель будет поражена не менее двух раз

Ответ: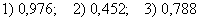

Автор: Емелин Александр

(Переход на главную страницу)

Качественные работы без плагиата – Zaochnik.com

mathprofi.ru