Среднеквадратическое (стандартное) отклонение

Определение

Среднеквадратическое отклонение (англ. Standard Deviation, SD) является показателем, который используется в теории вероятности и математической статистике для оценки степени рассеивания случайной величины относительно ее математического ожидания. В инвестировании стандартное отклонение доходности ценных бумаг или портфеля используется для оценки меры риска. Чем выше степень рассеивания доходности ценной бумаги относительно ожидаемого доходности (математическое ожидание доходности), тем выше риск инвестирования, и наоборот.

Среднеквадратическое отклонение как правило обозначается греческой буквой σ (сигма), а стандартное отклонение латинской буквой S или как Std(X), где X – случайная величина.

Истинное значение среднеквадратического отклонения

Если известно точное распределение дискретной случайной величины, а именно, известно ее значение при каждом исходе и может быть оценена вероятность каждого исхода, то формула расчета среднеквадратического отклонения будет выглядеть следующим образом.

Где Xi – значение случайной величины X при i-ом исходе; M(X) математическое ожидание случайной величины X; pi – вероятность i-го исхода; N – количество возможных исходов.

При этом математическое ожидание случайной величины рассчитывается по формуле:

Стандартное отклонение генеральной совокупности

На практике вместо точного распределение случайной величины обычно доступна только выборка данных. В этом случае рассчитывается оценочное значение среднеквадратического отклонения, которое в этом случае называют стандартным отклонением (S). Если оценка основывается на всей генеральной совокупности данных, необходимо использовать следующую формулу.

Где Xi – i-ое значение случайной величины X; X – среднеарифметическое генеральной совокупности; N – объем генеральной совокупности.

Стандартное отклонение выборки

Если используется не вся генеральная совокупность данных, а выборка из нее, то формула расчета стандартного отклонения основывается на несмещенной оценке дисперсии.

Где Xi – i-ое значение случайной величины X; X – среднеарифметическое выборки; N – объем выборки.

Примеры расчета

Портфельный менеджер должен оценить риски инвестирования в акции двух компаний А и Б. При этом он рассматривает 5 сценариев развития событий, информация по которым представлена в таблице.

Поскольку нам известно точное распределение доходности каждой из акций, мы можем рассчитать истинное значение среднеквадратического отклонения доходности для каждой из них.

Шаг 1. Рассчитаем математическое ожидание доходности для каждой из акций.

M(А) = -5%×0,02+6%×0,25+15%×0,40+24%×0,30+34%×0,03 = 15,62%

M(Б) = -18%×0,02+2%×0,25+16%×0,40+27%×0,30+36%×0,03 = 22,14%

Шаг 2. Подставим полученные данные в первую формулу.

Как мы можем видеть, акции Компании А характеризуются меньшим уровнем риска, поскольку у них ниже среднеквадратическое отклонение доходности. Следует также отметить, что и ожидаемая доходность у них ниже, чем у акций Компании Б.

Аналитик располагает данными о доходности двух ценных бумаг за последние 5 лет, которые представлены в таблице.

Поскольку точное распределение доходности неизвестно, а в распоряжении аналитика есть только выборка из генеральной совокупности данных, мы можем рассчитать стандартное отклонение выборки на основании несмещенной дисперсии.

Шаг 1. Рассчитаем ожидаемую доходность для каждой ценной бумаги как среднеарифметическое выборки.

X А = (7 + 15 + 2 – 5 + 6) ÷ 5 = 5%

X Б = (3 – 2 + 12 + 4 +8) ÷ 5 = 5%

Шаг 2. Рассчитаем стандартное отклонение доходности для каждой из ценных бумаг по формуле для выборки из генеральной совокупности данных.

Следует отметить, что обе ценные бумаги имеют равную ожидаемую доходность 5%. При этом стандартное отклонение доходности у ценной бумаги Б ниже, что при прочих равных делает ее более привлекательным объектом инвестирования в следствие лучшего профиля риск-доходность.

Стандартное отклонение в Excel

В Excel предусмотрено две функции для расчета стандартного отклонения выборки и генеральной совокупности.

Для выборки воспользуйтесь функцией «СТАНДОТКЛОН.В»:

  • В командной строке нажмите кнопку fx, во всплывшем окне «Вставка функции» выберите Категорию «Полный алфавитный перечень» и выберите функцию «СТАНДОТКЛОН.В».

    • Для генеральной совокупности используется функция «СТАНДОТКЛОН.Г»:

  1. В диапазоне ячеек B1:F1 введены значения случайной величины X.
  2. Выберите выходную ячейку B2.
  3. В командной строке нажмите кнопку fx, во всплывшем окне «Вставка функции» выберите Категорию «Полный алфавитный перечень» и выберите функцию «СТАНДОТКЛОН.Г».
  4. В поле «Число1» выберите диапазон ячеек B1:F1, поле «Число2» оставьте пустым и нажмите кнопку «OK».

Интерпретация

В инвестировании стандартное отклонение доходности используется в качестве меры волатильности. Чем выше его значение, тем выше риск, связанный с инвестированием в этот актив, и наоборот. При прочих равных параметрах, предпочтение следует отдавать тому активу, у которого этот показатель будет минимальным.

allfi.biz

Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки

Что такое стандартное отклонение — использование функции СТАНДОТКЛОН для расчета стандартного отклонения в Excel

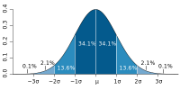
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.

Что измеряет стандартное отклонение?

Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.

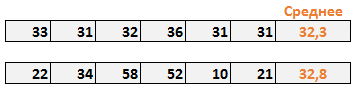
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.

Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.

В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.

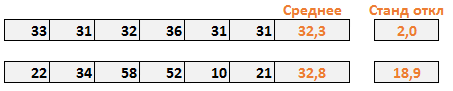
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.

В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.

Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.

Как рассчитать стандартное отклонение?

Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.

Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).

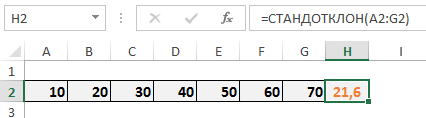
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.

Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.

Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.

Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.

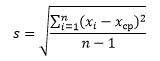
Функции расчета стандартного отклонения в Excel

В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.

Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.

Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.

Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.

Вам также могут быть интересны следующие статьи

25 комментариев

Ренат, добрый день.
Мне нравится статья, а главное способ подачи материала. Визуализация расчёта также порадовала новизной подхода, хотя и времени потребовала больше для понимания (классическое советское образование). Согласен, что про стандартное отклонение никто толком не знает, а зря…

Добрый день.
В формуле ошибка: под знаком корня необходимо суммировать квадраты отклонений

exceltip.ru

Процентное отклонение с отрицательным числом: формула Excel

Обычная формула для вычисления процентного отклонения прекрасно работает до той поры пока не приходиться работать с отрицательными числами. Проверьте стоит нам изменить значение в процентном отношении на отрицательное число в результате мы получаем ОШИБКУ! То есть формула процентного отклонения с отрицательным числом в числителе: = -10 /20-1 или так: =(20- -10 )/10 в любом случаи формулой будет возвращено ошибочное значение -300% . Возникает вопрос откуда появилось минус триста процентов ? Для ответа на этот вопрос и как делать правильно покажем на конкретном примере ниже.

Вычисление процентного отклонения для отрицательных чисел

Почти каждый инвестиционный проект пока еще не вышел на точку окупаемости в первый год приносит больше расходов чем доходов. Для этого при составлении бизнес-плана был заложен в бюджет объем просадки инвестиционного портфеля в пределах -10000$. Допустим объектом для инвестирования были криптовалюты биткоин и за первый очень успешный год доходность инвестиционного портфеля взлетела до +12000$. Вычисление процентного отклонения отношения между запланированной просадкой инвестиций и фактическим доходом по старой формуле: -10000/12000-1 дает -220%!

Почему же мы получили аж -220% отклонения? Ведь известно то, что доход не только перекрыл расходы и преодолел точку окупаемости, но и принес чистую прибыль в размере аж 12000$! Что ж, проблема возникает в том, что если значение отношения является отрицательным, то математическое вычисление возвращает обратный результат. В математике минус на минус всегда дает плюс, поэтому в нашей формуле нарушаются вычислительные операции. Часто такие ошибки допускаются при работе в Excel с бюджетами где запланированные расходы выражаются в отрицательных числах.

Для решения данной задачи следует использовать функцию =ABS(), которая преобразовывает отрицательное число в положительное. То есть, функция сама найдет модуль числа (его абсолютную величину). На рисунке показано как ведет себя модифицированная формула для вычисления процентного отклонения с отрицательными числами при любых условиях.

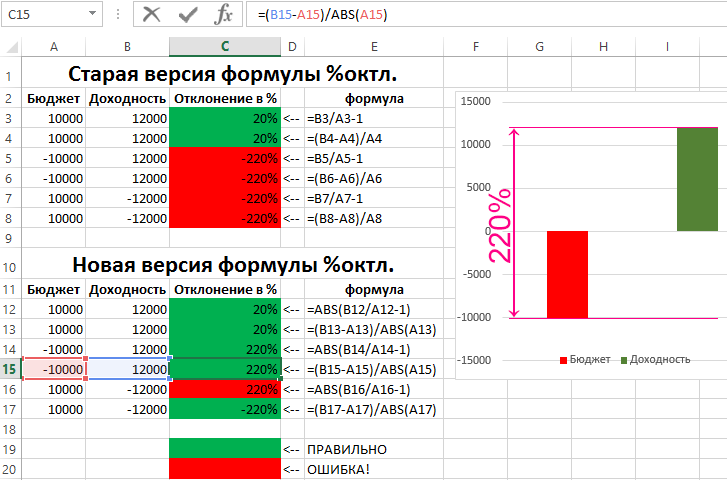
Как видите, чтобы вычисление процентного отклонения в Excel возвращало правильный результат при любых положительных или отрицательных числах в числителе и знаменателе следует использовать такую формулу:

На картинке видно, что доходности инвестиционного портфеля необходимо было преодолеть путь длинною в 220% (22000$), чтобы пройти от -10000$ до +12000$.

Из этого следует что доходность инвестиционного портфеля составила 120% годовых, потому как: (22000-10000)/10000=120%. А если мы при такой доходности инвестируем 10000$, то через год не только вернем вложенные средства, а еще и заработаем 12000$.

Интересный факт! На сегодняшний день среднестатистический показатель рискованных инвестиций составляет всего 70% годовых.

Эти формулы можно смело применять как при отрицательных, так и при положительных значениях. Процентное отклонение возвращается безошибочным в результате вычисления формулой с функцией ABS.

Описание примера работы функции ABS

Функция ABS возвращает абсолютное значение величины для любого числа. Если мы ведем в ячейке A1 формулу с функцией ABS в аргументах, которой будет указано отрицательное или положительное число, то в результате функция возвращает всегда только положительное число ABS(-100) = 100. Поэтому функция ABS, использованная в выше описанном примере, позволяет преобразовать отрицательнее число в положительное перед математическим вычислением для нахождения процентного отклонения (в данном случаи с отрицательным бюджетом -10 000$).

exceltable.com

Расчет отклонения фактического значения от планового (статус)

Статьи по теме

Один из важных шагов на пути к понятному и удобному отчету о движении денежных средств – предоставление пользователям информации об отклонениях плановых выплат и поступлений от фактических. Формула расчета отклонения приведена ниже.

Используйте пошаговые руководства:

Расчет отклонения фактического значения от планового (статус). Формула

Методические рекомендации по управлению финансами компании

Книги для Вашего профессионального роста

Подписка на статьи

Чтобы не пропустить ни одной важной или интересной статьи, подпишитесь на рассылку. Это бесплатно.

Проверь свои знания и приобрети новые

Самое выгодное предложение

Воспользуйтесь самым выгодным предложением на подписку и станьте читателем уже сейчас

Регламент контроля расходов на оплату труда

Чтобы избежать необоснованного роста затрат на персонал, закрепите в регламенте правила, по которым бухгалтерия рассчитывает премии сотрудникам.

Все для контроля долгов компании

Комплект рекомендаций, которые помогут повысить эффективность управления кредитным портфелем.

Самые популярные статьи месяца по версии редакции

Проверьте данные о собственнике компании

Выясните, есть ли данные о собственнике, из-за которых банк может отказать компании в кредите.

Как провести SWOT-анализ компании

Воспользуйтесь пошаговой инструкцией для проведения SWOT- анализа

Самые популярные статьи месяца: выбор читателей

Оценка финансовой устойчивости

Докажите кредиторам, что компании можно предоставлять длительную рассрочку платежа, убедите банк, что она справится с новыми кредитами и сможет вовремя расплатиться по всем своим обязательствам.

© 2007–2018 ООО «Актион управление и финансы»

«Финансовый директор» — практический журнал по управлению финансами компании

Все права защищены. Полное или частичное копирование любых материалов сайта возможно только с письменного разрешения редакции журнала «Финансовый директор».
Нарушение авторских прав влечет за собой ответственность в соответствии с законодательством РФ.

fd.ru

Правила расчета отклонений

Средняя арифметическая величина выборки

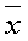
характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений:

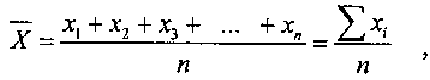
где 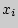— значение конкретного показателя,

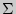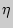— нак суммирования,

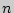— число показателей (случаев).

Практическое задание: рассчитать среднее арифметическое значение измерений силы кисти спортсмена по следующим результатам: 46, 50, 59, 60, 55, 49 кг.

Среднее арифметическое дает возможность:

1) охарактеризовать исследуемую совокупность одним числом;

2) сравнить отдельные величины со средним арифметическим;

3) определить тенденцию развития какого-либо явления;

4) сравнить разные совокупности;

5) вычислить другие статистические показатели, так как многие статистические вычисления опираются на среднее арифметическое.

Однако одно только среднее арифметическое не дает возможности глубоко анализировать сущность того или иного явления и их взаимные различия!

При анализе статистической совокупности одним из важных показателей является расположение значений элементов совокупности вокруг среднего значения (варьирование). Для характеристики варьирования в практике исследовательской работы рассчитывают среднее квадратическое (или стандартное) отклонение, которое отражает степень отклонения результатов от среднего значения, выражается в тех же единицах измерения.

Стандартное отклонение обозначается знаком 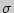(сигма) и вычисляется по формуле:

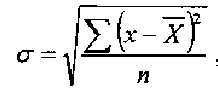
где 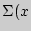— 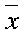) 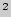— сумма разности квадратов между каждым показателем и средней арифметической величиной (сумма квадратов отклонений);

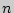— объем выборки (число измерений или испытуемых).

Если число измерений не более 30, т.е. 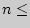30, используется формула:

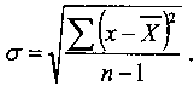
Порядок вычислений (1 вариант):

1. Заполнить первые две колонки таблицы расчетов (вычисление стандартного отклонения на примере показателей шести результатов измерения кистевой динамометрии).

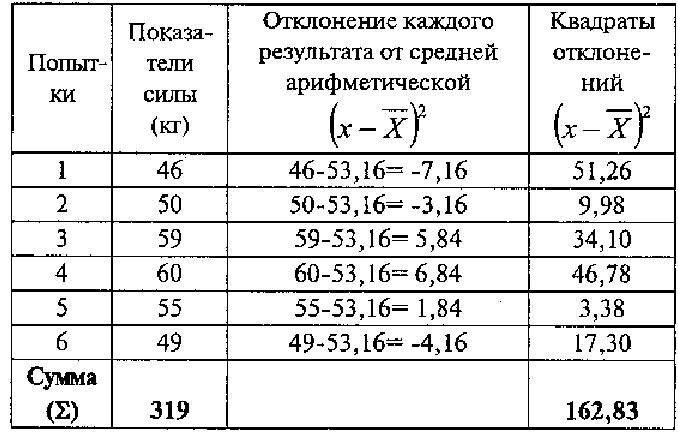
2. Рассчитать среднюю арифметическую величину:

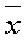
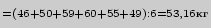
3. Вычислить разность между каждым показателем и данной средней (третья колонка таблицы).

4. Полученные разности возвести в квадрат и суммировать (четвертая колонка таблицы).

5. Вычислить среднее квадратическое отклонение по формуле:

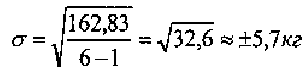
Порядок вычислений (2 вариант):

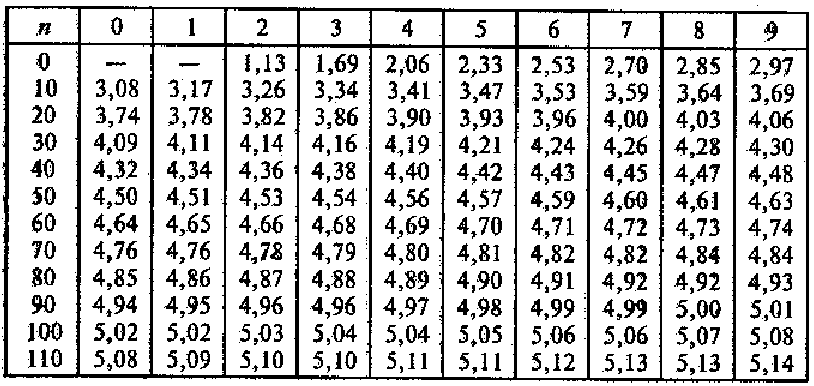
Более простой способ вычисления стандартного отклонения осуществляется по следующей формуле:

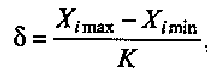
где 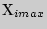—наибольшее значение показателя; Х 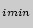— наименьшее значение показателя; 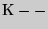табличный коэффициент (табл. 3).

Чем меньше величина 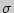, тем плотнее результаты около средней, что может говорить как о стабильности показателей одного испытуемого, так и ровности результатов группы или одинаковой подготовленности спортсменов.

Выборка результатов (какой бы она не была большой) не совпадает по абсолютной величине с соответствующими генеральными параметрами. Например, результаты физической подготовленности мастеров спорта одной спортивной школы не могут точно характеризовать результаты всех мастеров спорта страны. Величина отклонения выборочной средней от ее генерального параметра называется статистической стандартной ошибкой выборочного среднего арифметического. Иногда этот показатель называется просто ошибкой средней.

Этот показатель обозначается символом 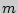и рассчитывается по формулам:

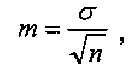
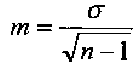
где 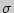— среднее квадратическое отклонение выборочной совокупности;

Значение стандартной ошибки средней арифметической ( 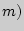указывает, насколько изменится среднее значение, если его перенести на всю генеральную совокупность.

Например, при измерениях у 20 спортсменов угла в коленном суставе ноги, стоящей на задней стартовой колодке, был получен следующий результат:

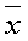
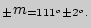
Это обозначает, что полученная средняя арифметическая величина 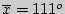в других аналогичных исследованиях может иметь значения от 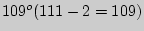до .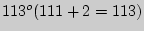

Практическое задание: студенты рассчитывают m среднего арифметического силы кисти руки спортсмена и делают вывод по следующим исходным данным:

cito-web.yspu.org