Деление дробей
Научившись умножать обыкновенные дроби, несложно научиться их делить. Как обычно, рассмотрим какие случаи могут нам встретиться при вычислении примеров на деление дробей.
Деление дроби на дробь
Чтобы разделить одну обыкновенную дробь на другую, отличную от нуля, нужно:
- числитель первой дроби умножить на знаменатель второй дроби и записать произведение в числитель новой дроби;
- знаменатель первой дроби умножить на числитель второй дроби и записать произведение в знаменатель новой дроби.
- во-первых, складываемые дроби приводятся к общему знаменателю (обычно, к наименьшему общему знаменателю);
- во-вторых, выполняется сложение полученных дробей с одинаковыми знаменателями.
- привести дроби к общему знаменателю (обычно дроби приводят к наименьшему общему знаменателю);
- вычесть полученные дроби с одинаковыми знаменателями.
Другими словами, деление дробей сводится к умножению. Поэтому правила деления дробей можно записать следующим образом.
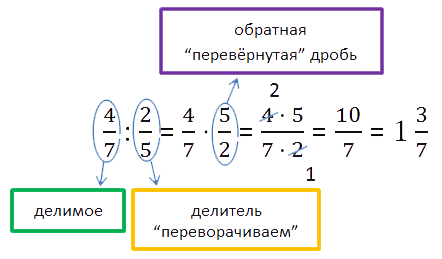
Чтобы разделить одну дробь на другую, надо делимое (первую дробь) умножить на обратную дробь делителю.
Как дробь разделить на число
Чтобы разделить дробь на натуральное число, можно использовать следующий способ.
Мы представляем натуральное число в виде неправильной дроби с числителем, равным самому числу, а знаменатель равным единице.
Затем призводим деление по правилу деления дроби на дробь.
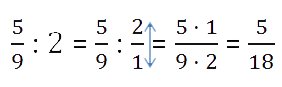
Деление смешанных чисел
При делении смешанных чисел надо представить числа в виде неправильных дробей, а потом разделить их друг на друга по правилу деления дроби на дроби.
math-prosto.ru
Сложение обыкновенных дробей: правила, примеры, решения.
Одним из действий с обыкновенными дробями является сложение. В этой статье мы разберемся, как осуществляется сложение обыкновенных дробей. Сначала рассмотрим сложение дробей с одинаковыми знаменателями, после этого изучим сложение дробей с разными знаменателями и подробно разберем решения примеров. Дальше остановимся на сложении обыкновенной дроби и натурального числа. Наконец, поговорим о сложении трех, четырех и большего количества обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Сначала разберем сложение дробей с одинаковыми знаменателями. Получить правило сложения дробей нам поможет следующий пример.
Пусть на тарелку положили три восьмых доли яблока и после этого еще две восьмых доли такого же яблока. Эти действия можно описать так: 3/8+2/8 . В результате на тарелке оказалось 3+2=5 восьмых долей яблока, то есть, 5/8 . Таким образом, сложение обыкновенных дробей 3/8 и 2/8 дает обыкновенную дробь 5/8 .
Из рассмотренного примера можно сделать вывод, что сложение дробей с одинаковыми знаменателями дает дробь, числитель которой равен сумме числителей складываемых дробей, а знаменатель равен знаменателям исходных дробей.
Итак, мы получили правило сложения дробей с одинаковыми знаменателями: при сложении дробей с одинаковыми знаменателями числители складываются, а знаменатель остается прежним.
Запишем это правило сложения дробей с помощью букв. Пусть нам нужно выполнить сложение обыкновенной дроби a/b и обыкновенной дроби c/b . Тогда, согласно правилу сложения дробей с одинаковыми знаменателями, справедливо равенство 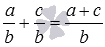 .
.
Осталось рассмотреть примеры сложения дробей с одинаковыми знаменателями.
Сложите обыкновенные дроби 5/23 и 7/23 .
Знаменатели складываемых дробей равны, поэтому в результате сложения будет дробь с таким же знаменателем 23 , а ее числитель будет равен сумме числителей складываемых дробей, то есть, 5+7=12 . Итак, сложение дробей 5/23 и 7/23 приводит нас к дроби 12/23 .
Кратко решение записывается так: 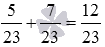 .
.
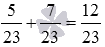 .
.
Если сложение дробей дает сократимую дробь (смотрите сократимые и несократимые дроби), то нужно провести сокращение дроби. Если при этом полученная дробь неправильная (смотрите правильные и неправильные дроби), то нужно выделить из нее целую часть.
Вычислите сумму обыкновенных дробей 5/28 и 3/28 .
Применив правило сложения дробей с одинаковыми знаменателями, получаем 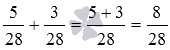 .
.
Очевидно, полученная дробь сократима, так как числитель и знаменатель делятся на 2 (при необходимости смотрите признак делимости на 2). Выполним сокращение дроби:  .
.
Таким образом, сложение дробей 5/28 и 3/28 дает 2/7 .
Приведем краткую запись всего решения: 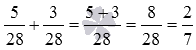 .
.
Выполните сложение обыкновенных дробей 15/62 и 140/62 .
Проведем сложение дробей с одинаковыми знаменателями: 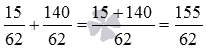 .
.
Проверим, можно ли сократить полученную дробь. Для этого вычислим наибольший общий делитель ее числителя и знаменателя, удобнее всего воспользоваться алгоритмом Евклида: 155=62·2+31 , 62=31·2 , следовательно, НОД(155, 62)=31 . Таким образом, дробь 144/62 можно сократить на 31 , имеем 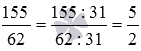 .
.
Очевидно, дробь 5/2 неправильная. Выполнив выделение целой части из неправильной дроби 5/2 , получаем 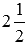 .
.
Итак, весь процесс сложения дробей с одинаковыми знаменателями 15/62 и 140/62 можно кратко записать так: .
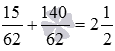 .
.
Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями можно свести к сложению дробей с одинаковыми знаменателями. Для этого достаточно складываемые дроби привести к общему знаменателю.
Исходя из этих соображений, получаем правило сложения дробей с разными знаменателями, которое содержит два шага:
Рассмотрим решения примеров, в которых выполняется сложение двух дробей с разными знаменателями.
Сложите обыкновенные дроби 5/8 и 1/12 .
Знаменатели складываемых дробей разные, поэтому, сначала нужно выполнить приведение дробей к наименьшему общему знаменателю. Для этого находим НОК(8, 12)=24 , находим соответствующие дополнительные множители 24:8=3 и 24:12=2 дробей 5/8 и 1/12 , в результате получаем 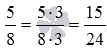 и
и 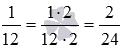 .
.
Теперь складываем дроби 15/24 и 2/24 , имеем 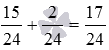 .
.
Таким образом, сложение дробей с разными знаменателями 5/8 и 1/12 дает дробь 7/24 .
Запишем все решение кратко: 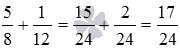 .
.
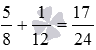 .
.
Заметим, если при сложении дробей получается сократимая дробь и (или) неправильная дробь, то нужно провести сокращение дроби и при возможности выделить целую часть.
Выполните сложение дробей с разными знаменателями 12/5 и 2/3 .
Для сложения дробей с разными знаменателями, сначала приведем их к наименьшему общему знаменателю: 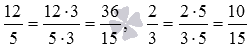 .
.
Теперь сложим дроби 36/15 и 10/15 , получаем 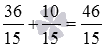 .
.
Проверим, не является ли полученная дробь сократимой. Для этого вычислим наибольший общий делитель числителя и знаменателя, воспользовавшись алгоритмом Евклида: 46=15·3+1 , 15=1·15 , следовательно, НОД(46, 15)=1 . Таким образом, дробь 46/15 несократима.
Но дробь 46/15 очевидно неправильная, поэтому из нее нужно выделить целую часть. Так как 46:15=3 (ост. 1) , то 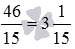 .
.
На этом сложение дробей с разными знаменателями завершено. Вот краткое решение: 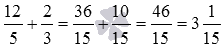 .
.
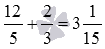 .
.
Сложение обыкновенной дроби и натурального числа
Сложение натурального числа с правильной обыкновенной дробью не представляет интереса, так как такая сумма по определению есть смешанное число. Например, 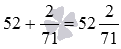 .
.
Сложение натурального числа с неправильной обыкновенной дробью можно проводить через сложение двух дробей, если натуральное число заменить дробью (смотрите натуральное число как дробь со знаменателем 1). К примеру, .
Однако, сложение натурального числа и неправильной дроби целесообразнее проводить, выделив из дроби целую часть. В результате сложение натурального числа и дроби сводится к сложению натурального числа и смешанного числа. Для примера вычислим сумму из предыдущего примера таким способом: 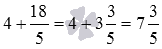 . Рассмотренный подход требует меньше вычислительной работы по сравнению с предыдущим способом, что особенно заметно, когда числа велики.
. Рассмотренный подход требует меньше вычислительной работы по сравнению с предыдущим способом, что особенно заметно, когда числа велики.
Сложение трех и большего количества обыкновенных дробей
Разберем, как сложить три, четыре и большее количество обыкновенных дробей.
Сложение обыкновенных дробей обладает переместительным и сочетательным свойствами. Это следует из определения обыкновенных дробей, а также из того, как мы определили сложение обыкновенных дробей. Таким образом, сложение трех, четырех и т.д. дробей можно проводить аналогично сложению трех большего количества натуральных чисел.
Сложите четыре обыкновенные дроби 5/12 , 13/12 , 1/12 и 1/12 .
Нам нужно вычислить сумму 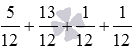 . Последовательно заменяя две соседние дроби их суммой, получим . Осталось лишь сократить полученную дробь, после чего выделить целую часть:
. Последовательно заменяя две соседние дроби их суммой, получим . Осталось лишь сократить полученную дробь, после чего выделить целую часть: 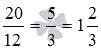 .
.
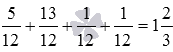 .
.
Аналогично проводится сложение нескольких натуральных чисел и нескольких обыкновенных дробей.
Вычислите сумму 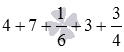 .
.
Свойства сложения позволяют провести следующую группировку слагаемых: . Сумма трех натуральных чисел в скобках равна 14 , а сумма 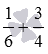 равна дроби 11/12 . Таким образом, .
равна дроби 11/12 . Таким образом, .
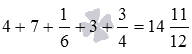 .
.
Стоит отметить, что и правило сложения дробей с одинаковыми знаменателями, и правило сложения дробей с разными знаменателями остаются справедливыми для трех и большего количества складываемых дробей.
Рассмотрим решение одного из предыдущих примеров в этом свете.
Обратившись к правилу сложения дробей с одинаковыми знаменателями, получаем . Осталось лишь сократить полученную дробь, после чего выделить целую часть: 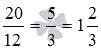 .
.
Сложите три дроби с разными знаменателями 1/2 , 3/8 и 7/12 .
Сначала выполним приведение трех дробей к наименьшему общему знаменателю (смотрите приведение к общему знаменателю трех и большего количества дробей), получаем .
Осталось лишь закончить сложение: .
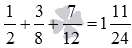 .
.
www.cleverstudents.ru
Вычитание обыкновенных дробей: правила, примеры, решения.
Продолжаем изучать действия с обыкновенными дробями. Здесь мы разберемся, как проводится вычитание обыкновенных дробей. Сначала получим правило вычитания дробей с одинаковыми знаменателями. Дальше рассмотрим вычитание дробей с разными знаменателями и приведем примеры вычитания с подробными решениями. После этого остановимся на вычитании дроби из натурального числа и вычитании числа из дроби. В заключение покажем, как проводится вычитание обыкновенных дробей с использованием свойств этого действия.
Сразу заметим, что в этой статье мы будем говорить лишь о вычитании меньшей дроби из большей дроби. Другие случаи разобраны в статье вычитание рациональных чисел.
Навигация по странице.
Вычитание дробей с одинаковыми знаменателями
Для начала приведем пример, который позволит нам выяснить, как проводится вычитание дробей с одинаковыми знаменателями.
Пусть на тарелке находилось пять восьмых долей яблока, то есть, 5/8 яблока, после чего две восьмых доли забрали. По смыслу вычитания (смотрите общее представление о вычитании), указанное действие описывается так:  . Понятно, что при этом на тарелке остается 5−2=3 восьмых доли яблока. То есть,
. Понятно, что при этом на тарелке остается 5−2=3 восьмых доли яблока. То есть,  .
.
Рассмотренный пример иллюстрирует правило вычитания дробей с одинаковыми знаменателями: при вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитается числитель вычитаемого, а знаменатель остается прежним.
Озвученное правило с помощью букв записывается так:  . Эту формулу и будем использовать при вычитании дробей с одинаковыми знаменателями.
. Эту формулу и будем использовать при вычитании дробей с одинаковыми знаменателями.
Рассмотрим примеры вычитания дробей с одинаковыми знаменателями.
Выполните вычитание обыкновенной дроби 17/15 из обыкновенной дроби 24/15 .
Знаменатели вычитаемых дробей равны. Числитель уменьшаемого равен 24 , а числитель вычитаемого равен 17 , их разность равна 7 ( 24−17=7 при необходимости смотрите вычитание натуральных чисел). Поэтому вычитание дробей с одинаковыми знаменателями 24/15 и 17/15 дает дробь 7/15 .
Краткий вариант решения выглядит так:  .
.
 .
.
При возможности нужно проводить сокращение дроби и (или) выделение целой части из неправильной дроби, которая получается при вычитании дробей с одинаковыми знаменателями.
Вычислите разность  .
.
Воспользуемся формулой вычитания дробей с одинаковыми знаменателями:  .
.
Очевидно, числитель и знаменатель полученной дроби делятся на 2 (смотрите признак делимости на 2), то есть, 22/12 – сократимая дробь. Выполнив сокращение этой дроби на 2 , приходим к дроби 11/6 .
Дробь 11/6 – неправильная (смотрите правильные и неправильные дроби). Поэтому из нее нужно выделить целую часть:  .
.
Итак, вычисляемая разность дробей с одинаковыми знаменателями равна  .
.
Вот все решение:  .
.
 .
.
Вычитание дробей с разными знаменателями
Вычитание дробей с разными знаменателями сводится к вычитанию дробей с одинаковыми знаменателями. Для этого дроби с разными знаменателями достаточно привести к общему знаменателю.
Итак, чтобы провести вычитание дробей с разными знаменателями, надо:
Рассмотрим примеры вычитания дробей с разными знаменателями.
Отнимите от обыкновенной дроби 2/9 обыкновенную дробь 1/15 .
Так как знаменатели вычитаемых дробей разные, то сначала выполним приведение дробей к наименьшему общему знаменателю: так как НОК(9, 15)=45 , то дополнительным множителем дроби 2/9 является число 45:9=5 , а дополнительным множителем дроби 1/15 является число 45:15=3 , тогда  и
и  .
.
Осталось вычесть из дроби 10/45 дробь 3/45 , получаем  , что и дает нам искомую разность дробей с разными знаменателями.
, что и дает нам искомую разность дробей с разными знаменателями.
Кратко решение записывается так:  .
.
 .
.
Не следует забывать про сокращение полученной после вычитания дроби, а также про выделение целой части.
Вычтите из дроби 19/9 дробь 7/36 .
После приведения дробей с разными знаменателями к наименьшему общему знаменателю 36 , имеем дроби 76/9 и 7/36 . Вычисляем их разность:  .
.
Полученная дробь сократима, после ее сокращения на 3 , получаем 23/12 . А эта дробь неправильная, выделив из нее целую часть, имеем  .
.
Соберем воедино все выполненные действия при вычитании исходных дробей с разными знаменателями: .
 .
.
Вычитание натурального числа из обыкновенной дроби
Вычитание натурального числа из дроби можно свести к вычитанию обыкновенных дробей. Для этого достаточно представить натуральное число в виде дроби со знаменателем 1. Разберем решение примера.
Выполните вычитание числа 3 из дроби 83/21 .
Так как число 3 равно дроби 3/1 , то .
 .
.
Однако вычитание натурального числа из неправильной дроби удобнее проводить, представив дробь в виде смешанного числа. Покажем решение предыдущего примера этим способом.
Отнимите число 3 от дроби 83/21 .
Сначала выделим целую часть из неправильной дроби 83/21 , имеем  , тогда
, тогда  . Осталось провести вычитание натурального числа из смешанного числа:
. Осталось провести вычитание натурального числа из смешанного числа:  .
.
 .
.
Вычитание обыкновенной дроби из натурального числа
Вычитание обыкновенной дроби из натурального числа можно свести к вычитанию обыкновенных дробей, представив натуральное число как дробь. Разберем решение примера, иллюстрирующего такой подход.
Отнимите обыкновенную дробь 5/3 от натурального числа 7 .
Представим число 7 как дробь 7/1 , после чего выполним вычитание: .
Выделив целую часть из полученной дроби, получаем окончательный ответ  .
.
 .
.
Однако существует более рациональный способ вычитания дроби из натурального числа. Его преимущества особенно заметны, когда уменьшаемое натуральное число и знаменатель вычитаемой дроби являются большими числами. Все это будет видно из примеров ниже.
Если вычитаемая дробь правильная, то уменьшаемое натуральное число можно заменить суммой двух чисел, одно из которых равно единице, отнять правильную дробь от единицы, после чего завершить вычисления.
Выполните вычитание обыкновенной дроби 13/62 из натурального числа 1 065 .
Вычитаемая обыкновенная дробь – правильная. Заменим число 1 065 суммой 1 064+1 , при этом получим  . Осталось вычислить значение полученного выражения (подробнее о вычислении таких выражений мы поговорим в следующем пункте).
. Осталось вычислить значение полученного выражения (подробнее о вычислении таких выражений мы поговорим в следующем пункте).
В силу свойств вычитания, полученное выражение можно переписать как  . Вычислим значение разности в скобках, заменив единицу дробью 1/1 , имеем
. Вычислим значение разности в скобках, заменив единицу дробью 1/1 , имеем  . Таким образом, . На этом вычитание дроби 13/62 из натурального числа 1 065 завершено.
. Таким образом, . На этом вычитание дроби 13/62 из натурального числа 1 065 завершено.
Вот все решение:
А теперь для сравнения покажем, с какими числами нам бы пришлось работать, если бы мы решили свести вычитание исходных чисел к вычитанию дробей:
 .
.
Если же вычитаемая дробь неправильная, то ее можно заменить смешанным числом, после чего провести вычитание смешанного числа из натурального числа.
Отнимите от натурального числа 644 дробь 73/5 .
Выделим целую часть из неправильной дроби:  . Тогда .
. Тогда .
Осталось лишь выполнить вычитание правильной дроби из натурального числа, поступим также как в предыдущем примере: .
 .
.
Использование свойств вычитания при вычитании дробей
Для вычитания обыкновенных дробей справедливы все свойства вычитания натуральных чисел. Это следует из смысла, который мы придали обыкновенным дробям и операции вычитания дробей. Свойства вычитания позволяют вычислять значения выражений с дробями. Рассмотрим примеры.
Вычислите значение выражения  .
.
Решения подобных примеров с натуральными числами разобраны в разделе вычитание суммы из числа. Здесь будем действовать аналогично.
Сначала вычислим разность  , после чего от нее отнимем дробь 5/6 . Итак,
, после чего от нее отнимем дробь 5/6 . Итак,  и
и  . После выделения целой части из полученной неправильной дроби получаем
. После выделения целой части из полученной неправильной дроби получаем  .
.
Так выглядит краткая запись решения: .
 .
.
Когда выражение содержит и натуральные числа и дроби, то при вычислении удобно группировать числа с числами, а дроби с дробями.
Выполните вычитание суммы натурального числа и обыкновенной дроби  из суммы натурального числа и обыкновенной дроби
из суммы натурального числа и обыкновенной дроби  .
.
Нам нужно вычислить разность  . Свойства сложения и вычитания позволяют нам провести следующую группировку , что упрощает вычисления. Осталось лишь закончить вычисления: .
. Свойства сложения и вычитания позволяют нам провести следующую группировку , что упрощает вычисления. Осталось лишь закончить вычисления: .
 .
.
Действия с обыкновенными дробями
Расширение дроби. Сокращение дроби. Сравнение дробей.
Приведение к общему знаменателю. Сложение и вычитание дробей.
Умножение дробей. Деление дробей.
Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется расширением дроби. Например,
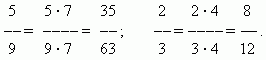
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется сокращением дроби. Например,
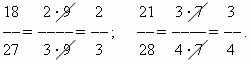
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:
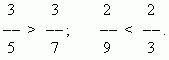
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:
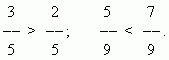
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.
П р и м е р . Сравнить две дроби:
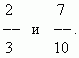
Расширим первую дробь на знаменатель второй , а вторую — на знаменатель первой:

Использованное здесь преобразование называется приведением дробей к общему знаменателю.
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
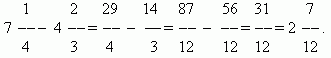
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.
П р и м е р . 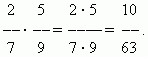
Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь . Это правило вытекает из определения деления (см. раздел «Арифметические операции»).
П р и м е р . 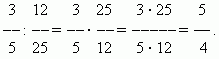
www.bymath.net