Порядок выполнения действий, правила, примеры.
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
- Ввести частные случаи умножения с 0 и 1.
- Закрепить смысл умножения и переместительное свойство умножения, отрабатывать вычислительные навыки.
- Развивать внимание, память, мыслительные операции, речь, творческие способности, интерес к математике.
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: 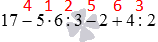 .
.
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2 :3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
www.cleverstudents.ru
Умножение на 0 и 1. 3-й класс
Презентация к уроку
Загрузить презентацию (489,5 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Оборудование: Слайдовая презентация: Приложение1.
1. Организационный момент.
Сегодня у нас необычный день. На уроке присутствуют гости. Порадуйте меня, друзей, гостей своими успехами. Откройте тетради, запишите число, классная работа. На полях отметьте свое настроение в начале урока. Слайд 2.

Устно весь класс повторяет таблицу умножения на карточках с проговариванием вслух (неправильные ответы дети отмечают хлопками).
Физкультминутка (“Мозговая гимнастика”, “Шапка для размышления”, на дыхание).
2. Постановка учебной задачи.
2.1. Задания на развитие внимания.
На доске и на столе у детей двухцветная картинка с числами:
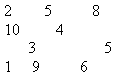
– Что интересного в записанных числах? (Записаны разными цветами; все “красные” числа – четные, а “синие” – нечетные.)
– Какое число лишнее? (10 – круглое, а остальные нет; 10 – двузначное, а остальные однозначные; 5 – повторяется два раза, а остальные – по одному.)
– Закрою число 10. Есть ли лишнее среди остальных чисел? (3 – у него нет пары до 10, а у остальных есть.)
– Найдите сумму всех “красных” чисел и запишите ее в красном квадрате. (30.)
– Найдите сумму всех “синих” чисел и запишите ее в синем квадрате. (23.)
– На сколько 30 больше, чем 23? (На 7.)
– На сколько 23 меньше, чем 30? (Тоже на 7.)
– Каким действием искали? (Вычитанием.) Слайд 3.
2.2. Задания на развитие памяти и речи. Актуализация знаний.
а) – Повторите по порядку слова, которые я назову: слагаемое, слагаемое, сумма, уменьшаемое, вычитаемое, разность. (Дети пытаются воспроизвести порядок слов.)
– Компоненты каких действий назвали? (Сложение и вычитание.)
– С каким действием вы еще знакомы? (Умножение, деление.)
– Назовите компоненты умножения. (Множитель, множитель, произведение.)
– Что обозначает первый множитель? (Равные слагаемые в сумме.)
– Что обозначает второй множитель? (Число таких слагаемых.)
Запишите определение умножения.
б) – Рассмотрите записи. Какое задание будете выполнять?
12 + 12 + 12 + 12 + 12
33 + 33 + 33 + 33
а + а + а
(Заменить сумму произведением.)
Что получится? (В первом выражении 5 слагаемых, каждый из которых равен 12, поэтому оно равно 12•5. Аналогично – 33•4, а•3)
в) – Назовите обратную операцию. (Заменить произведение суммой.)
– Замените произведение суммой в выражениях: 99•2. 8•4. Ь•3. (99 + 99, 8 + 8 + 8 + 8, b + b + b). Слайд 4.
г) На доске записаны равенства:
81 + 81 = 81 – 2
21•3 = 21 + 22 + 23
44 + 44 + 44 + 44 = 44 + 4
17 + 17 – 17 + 17 – 17 = 17•5
Рядом с каждым равенством помещаются картинки.
– Зверюшки лесной школы выполняли задание. Правильно ли они его выполнили?
Дети устанавливают, что слон, тигр, заяц и белка ошиблись, объясняют, в чем их ошибки. Слайд 5.
д) Сравните выражения:
8•5. 5•8
5•6. 3•6
34•9… 31•2
а•3. а•2 + а
(8•5 = 5•8, так как от перестановки слагаемых сумма не изменяется;
5•6 > 3•6, так как слева и справа по 6 слагаемых, но слева слагаемые больше;
34•9 > 31•2. так как слева слагаемых больше и сами слагаемые больше;
а•3 = а•2 + а, так как слева и справа по 3 слагаемых, равных а.)
– Какое свойство умножения использовали в первом примере? (Переместительное.) Слайд 6.
2.3. Постановка проблемы. Целеполагание.
Верны ли равенства? Почему? (Верны, так как сумма 5 + 5 + 5 = 15. потом в сумме становится на одно слагаемое 5 больше, и сумма увеличивается на 5.)
5•3 = 15
5•4 = 20
5•5 = 25
5•6 = 30
– Продолжите эту закономерность направо. (5•7 = 35; 5•8 = 40. )
– Продолжите ее теперь налево. (5•2 = 10; 5•1=5; 5•0 = 0.)
– А что означает выражение 5•1? 5•0? (? Проблема!)
– В нашем примере было бы удобно считать, что 5•1 = 5, а 5•0 = 0.
Однако выражения 5•1 и 5•0 не имеют смысла. Мы можем условиться считать эти равенства верными. Но для этого надо проверить, не нарушим ли мы переместительное свойство умножения.
Итак, цель нашего урока – установить, сможем ли мы считать равенства 5•1 = 5 и 5•0 = 0 верными?
– Проблема урока! Слайд 7.
3. “Открытие” детьми нового знания.
а) – Выполните действия: 1•7, 1•4, 1•5.
Дети решают примеры с комментированием в тетради и на доске:
1•7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7
1•4 = 1 + 1 + 1 + 1 = 4
1•5 = 1 + 1 + 1 + 1 +1 = 5
– Сделайте вывод: 1•а – ? (1•а = а.) Выставляется карточка: 1•а = а
б) – Имеют ли смысл выражения 7•1, 4•1, 5•1? Почему? (Нет, так как в сумме не может быть одно слагаемое.)
– Чему они должны быть равны, чтобы не нарушалось переместительное свойство умножения? (7 • 1 тоже должно быть равно 7, поэтому 7 • 1 = 7.)
Аналогично рассматриваются 4•1 = 4; 5•1 = 5.
– Сделайте вывод: а•1 = ? (а•1 = а.)
Выставляется карточка: а•1 = а. Накладывается первая карточка на вторую: а•1 = 1•а = а.
– Совпадает наш вывод с тем, что у нас получилось на числовом луче? (Да.)
– Переведите это равенство на русский язык. (При умножении числа на 1 или 1 на число получается то же самое число.)
– Молодцы! Итак, будем считать: а•1 = 1•а = а. Слайд 8.
2) Аналогично исследуется случай умножения с 0. Вывод:
– при умножении числа на 0 или 0 на число получается нуль: а • 0 = 0 • а = 0. Слайд 9.
– Сравните оба равенства: что вам напоминают 0 и 1?
Дети высказывают свои версии. Можно обратить их внимание на образы:
1 – “зеркальце”, 0 – “страшный зверь” или “шапка-невидимка”.
Молодцы! Итак, при умножении на 1 получается то же самое число (1 – “зеркальце”), а при умножении на 0 получается 0 (0 – “шапка-невидимка”).
4. Физкультминутка (для глаз – “круг”, “вверх – вниз”, для рук – “замок”, “кулачки”).
5. Первичное закрепление.
На доске записаны примеры:
Дети решают их в тетради и на доске с проговариванием в громкой речи полученных правил, например:
3 • 1 = 3, так как при умножении числа на 1 получается то же самое число (1 – “зеркальце”), и т.д.
а) 145•х = 145; б) х•437 = 437.
– При умножении 145 на неизвестное число получилось 145. Значит, умножали на 1•х = 1. И т.д.
– При умножении 8 на неизвестное число получился 0. Значит, умножали на 0•х = 0. И т.д.
6. Самостоятельная работа с проверкой в классе. Слайд 10.
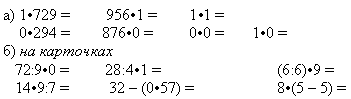
Дети самостоятельно решают записанные примеры. Затем по готовому
образцу проверяют свои ответы с проговариванием в громкой речи, отмечают правильно решенные примеры плюсом, исправляют допущенные ошибки. Те, кто допустил ошибки, получают аналогичное задание на карточке и дорабатывают индивидуально, пока класс решает задачи на повторение.
7. Задачи на повторение. (Работа в парах). Слайд 11.
а) – Хотите узнать что вас ждет в будущем? Вы это узнаете, расшифровав запись:
xn--i1abbnckbmcl9fb.xn--p1ai
Порядок арифметических действий, скобки
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1
Сначала выполняем действия в скобках:
16 — 2 · 7 + 4 = 16 — 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 — 2 · 6 + 6 · 7 =
= 9 + 4 — 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 — 6 = 2
10 — 2 · 3 = 10 — 6 = 4
действия в квадратных скобках дают:
14 — 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 — 20 = 10
35 — 10 = 25
100 — 25 = 75
75 · 2 = 150
m.fxyz.ru
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё, что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателями
Сложение дробей бывает двух видов:
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби  и
и  . Складываем числители, а знаменатель оставляем без изменения:
. Складываем числители, а знаменатель оставляем без изменения:
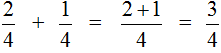
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к  пиццы прибавить
пиццы прибавить  пиццы, то получится
пиццы, то получится 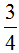 пиццы:
пиццы:

Пример 2. Сложить дроби  и
и  .
.
Опять же складываем числители, а знаменатель оставляем без изменения:
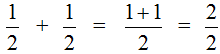
В ответе получилась неправильная дробь 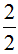 . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
. Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
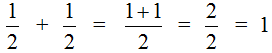
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к  пиццы прибавить еще
пиццы прибавить еще  пиццы, то получится одна целая пицца:
пиццы, то получится одна целая пицца:

Пример 3. Сложить дроби  и
и  .
.
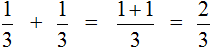
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к  пиццы прибавить ещё
пиццы прибавить ещё  пиццы, то получится
пиццы, то получится  пиццы:
пиццы:

Пример 4. Найти значение выражения 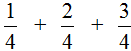
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
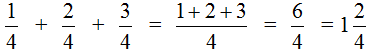
Попробуем изобразить наше решение с помощью рисунка. Если к  пиццы прибавить
пиццы прибавить  пиццы и ещё прибавить пиццы, то получится 1 целая и ещё
пиццы и ещё прибавить пиццы, то получится 1 целая и ещё  пиццы.
пиццы.

Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить прежним;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби
 и
и  сложить можно, поскольку у них одинаковые знаменатели.
сложить можно, поскольку у них одинаковые знаменатели.А вот дроби
 и
и  сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и

В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и
 . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
. Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
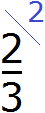
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
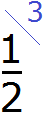
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
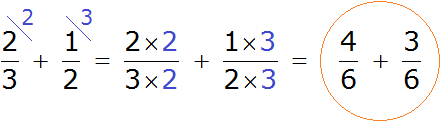
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
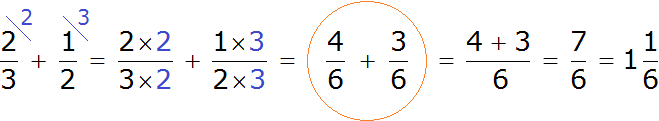
Таким образом, пример завершается. К прибавить
 получается
получается 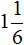 .
.Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить
 пиццы, то получится одна целая пицца и еще одна шестая пиццы:
пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и
 к общему знаменателю, мы получили дроби
к общему знаменателю, мы получили дроби  и
и  . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
. Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).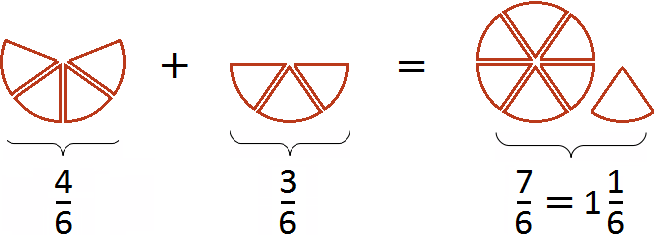
Первый рисунок изображает дробь
 (четыре кусочка из шести), а второй рисунок изображает дробь
(четыре кусочка из шести), а второй рисунок изображает дробь  (три кусочка из шести). Сложив эти кусочки мы получаем
(три кусочка из шести). Сложив эти кусочки мы получаем 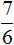 (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили
(семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили 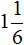 (одну целую пиццу и еще одну шестую пиццы).
(одну целую пиццу и еще одну шестую пиццы).Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
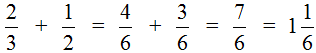
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения
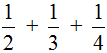 .
.Воспользуемся схемой, которую мы привели выше.
Шаг 1. Найти НОК для знаменателей дробей
Находим НОК для знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4. Нужно найти НОК для этих чисел:




Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
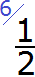
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
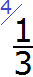
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
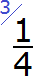
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
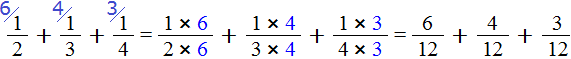
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
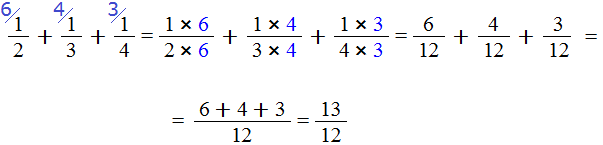
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить её целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
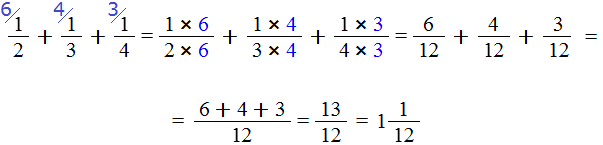
Получили ответ
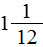
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения
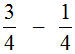 . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Так и сделаем:
. Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Так и сделаем: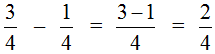
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от
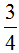 пиццы отрезать
пиццы отрезать  пиццы, то получится
пиццы, то получится  пиццы:
пиццы:
Пример 2. Найти значение выражения
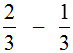 .
.Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем прежним:
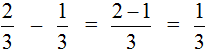
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от
 пиццы отрезать
пиццы отрезать  пиццы, то получится
пиццы, то получится  пиццы:
пиццы:
Пример 3. Найти значение выражения
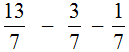
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
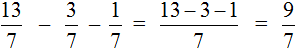
В ответе получилась неправильная дробь. Если пример завершен, то от неправильной дроби принято избавляться. Давайте и мы избавимся от неправильной дроби в ответе. Для этого выделим ее целую часть:
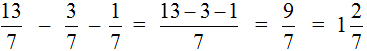
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним;
- Если в ответе получилась неправильная дробь, то нужно выделить её целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби
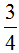 можно вычесть дробь
можно вычесть дробь  , поскольку у этих дробей одинаковые знаменатели. А вот от дроби
, поскольку у этих дробей одинаковые знаменатели. А вот от дроби  нельзя вычесть дробь
нельзя вычесть дробь  , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
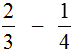
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям
 и
и 
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
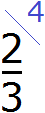
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
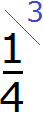
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
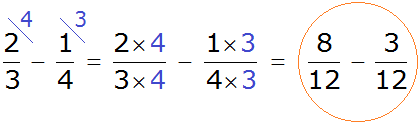
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
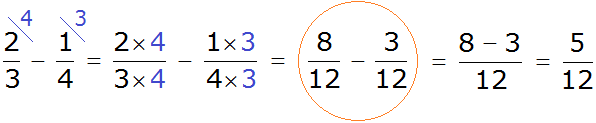
Получили ответ
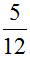
Попробуем изобразить наше решение с помощью рисунка. Если от
 пиццы отрезать
пиццы отрезать  пиццы, то получится
пиццы, то получится 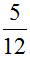 пиццы
пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
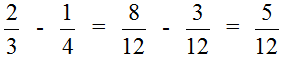
Приведение дробей
 и
и  к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби
к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби 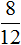 и
и 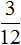 . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
. Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):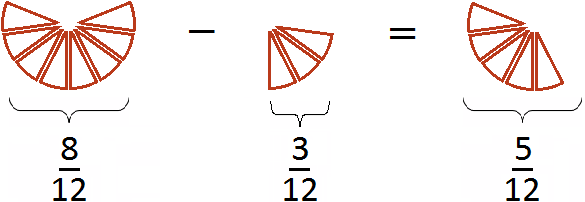
Первый рисунок изображает дробь
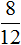 (восемь кусочков из двенадцати), а второй рисунок — дробь
(восемь кусочков из двенадцати), а второй рисунок — дробь 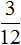 (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь
(три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь 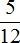 и описывает эти пять кусочков.
и описывает эти пять кусочков.Пример 2. Найти значение выражения
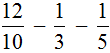
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
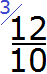
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
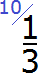
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
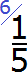
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
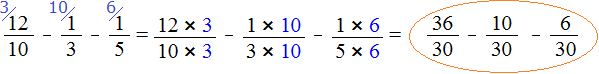
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
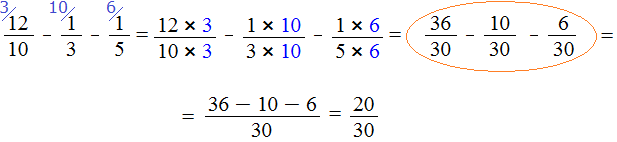
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще и эстетичнее. А что можно сделать? Можно сократить эту дробь. Напомним, что сокращением дроби называется деление числителя и знаменателя на наибольший общий делитель числителя и знаменателя.
Чтобы грамотно сократить дробь
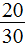 нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.Нельзя путать НОД с НОК. Самая распространённая ошибка многих новичков. НОД — это наибольший общий делитель. Его мы находим для сокращения дроби.
А НОК — это наименьшее общее кратное. Его мы находим для того, чтобы привести дроби к одинаковому (общему) знаменателю.
Сейчас мы будем находить наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД для чисел 20 и 30:



НОД (20 и 30) = 10
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби
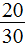 на 10:
на 10: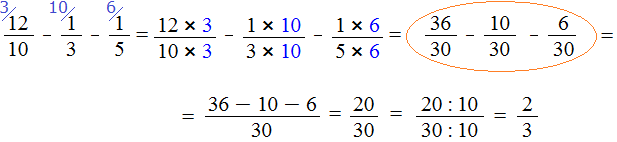
Получили красивый ответ

Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1. Умножить дробь
 на число 1 .
на число 1 .Умножим числитель дроби
 на число 1
на число 1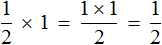
Запись
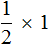 можно понимать, как взять половину 1 раз. К примеру, если
можно понимать, как взять половину 1 раз. К примеру, если  пиццы взять 1 раз, то получится
пиццы взять 1 раз, то получится  пиццы
пиццы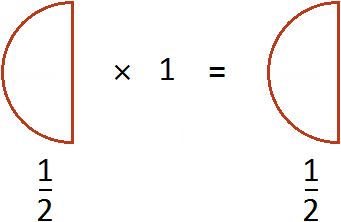
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение
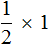 , записать как
, записать как 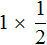 , то произведение по прежнему будет равно
, то произведение по прежнему будет равно  . Опять же срабатывает правило перемножения целого числа и дроби:
. Опять же срабатывает правило перемножения целого числа и дроби: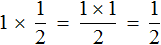
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется
 пиццы:
пиццы: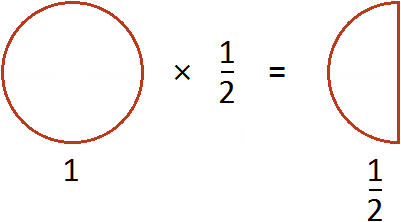
Пример 2. Найти значение выражения
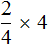
Умножим числитель дроби
 на 4
на 4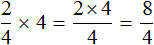
В ответе получилась неправильная дробь. Выделим в ней целую часть:
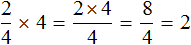
Выражение
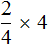 можно понимать, как взятие двух четвертей 4 раза. К примеру, если
можно понимать, как взятие двух четвертей 4 раза. К примеру, если  пиццы взять 4 раза, то получится две целые пиццы
пиццы взять 4 раза, то получится две целые пиццы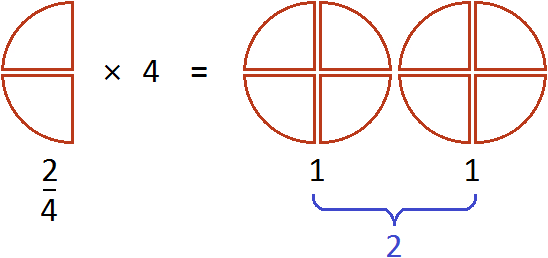
А если поменять множимое и множитель местами, то получим выражение
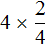 . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
. Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц: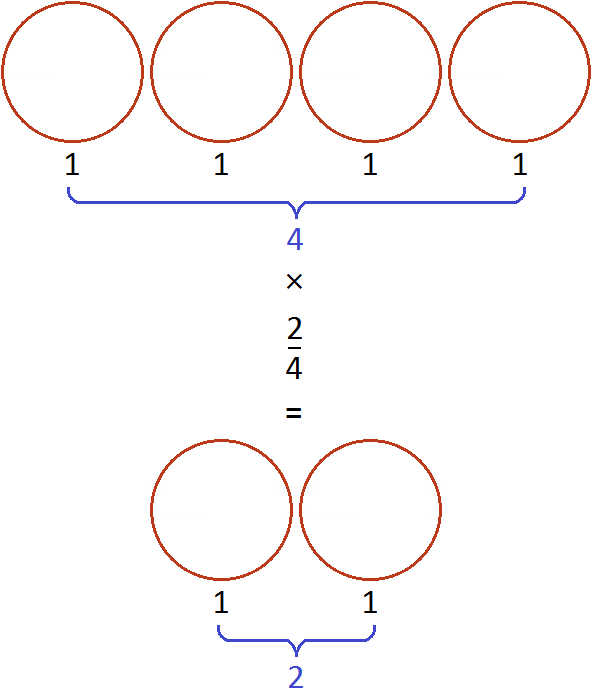
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения
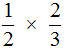 .
.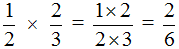
Получили ответ
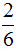 . Желательно сократить данную дробь. Дробь
. Желательно сократить данную дробь. Дробь 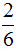 можно сократить на 2. Тогда окончательное решение примет следующий вид:
можно сократить на 2. Тогда окончательное решение примет следующий вид: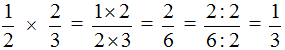
Выражение
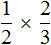 можно понимать, как взятие пиццы от половины пиццы. Допустим у нас есть половина пиццы:
можно понимать, как взятие пиццы от половины пиццы. Допустим у нас есть половина пиццы:Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:
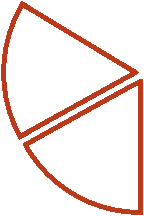
У нас получится
 пиццы. Вспомните, как выглядит пицца, разделенная на три части:
пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
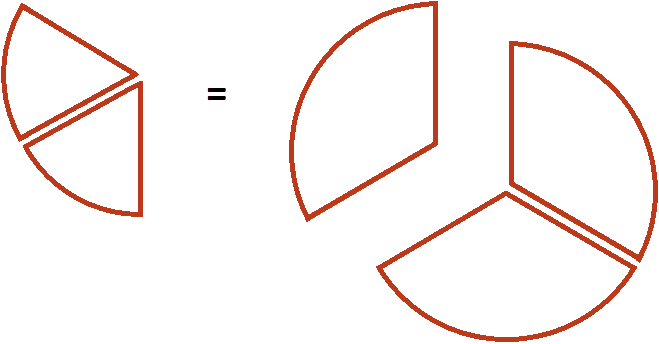
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения
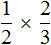 равно
равно 
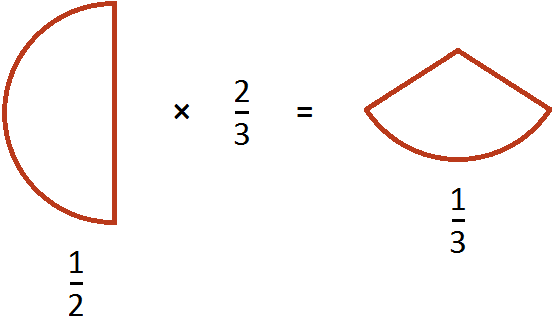
Пример 2. Найти значение выражения
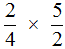
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
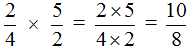
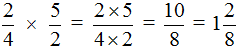
Пример 3. Найти значение выражения
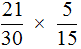
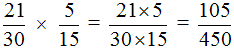
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя. Итак, найдём НОД чисел 105 и 450:



НОД для (105 и 150) равен 15
Теперь делим числитель и знаменатель нашего ответа на НОД:
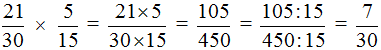
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как
 . От этого пятёрка своего значения не поменяет, поскольку выражение
. От этого пятёрка своего значения не поменяет, поскольку выражение  означает «число пять разделить на единицу», а это, как известно равно пятёрке:
означает «число пять разделить на единицу», а это, как известно равно пятёрке: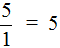
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:

Затем умножить эту дробь на саму себя, только поменять местами числитель и знаменатель. Другими словами, умножить дробь
 на саму себя, только перевёрнутую:
на саму себя, только перевёрнутую: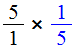
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
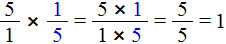
Значит обратным к числу 5, является число
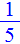 , поскольку при умножении 5 на
, поскольку при умножении 5 на 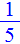 получается единица.
получается единица.Обратное число можно найти также для любого другого целого числа.
- обратным числа 2 является дробь

- обратным числа 2 является дробь
- обратным числа 3 является дробь

- обратным числа 4 является дробь

- для дроби
 обратной дробью является дробь
обратной дробью является дробь 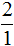
- для для дроби
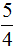 обратной дробью является дробь
обратной дробью является дробь 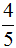
- для дроби
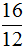 обратной дробью является дробь
обратной дробью является дробь 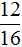
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?
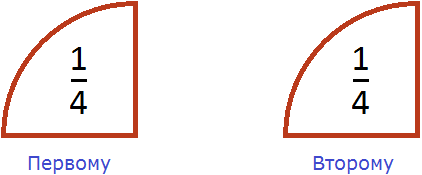
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет
 пиццы. Значит каждому достанется по
пиццы. Значит каждому достанется по  пиццы.
пиццы.Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь
 на число 2 . Здесь делимым является дробь
на число 2 . Здесь делимым является дробь  , а делителем число 2.
, а делителем число 2.Чтобы разделить дробь
 на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь
на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь  . Значит нужно умножить
. Значит нужно умножить  на
на 
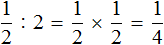
Получили ответ
 . Значит при делении половины на две части получается четверть.
. Значит при делении половины на две части получается четверть.Попробуем понять сам механизм деления дробей. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
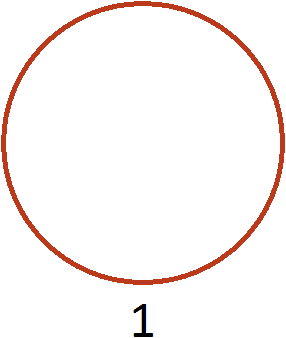
Умножим её на 2. То есть, повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть, разделим 2 пиццы на 2. Тогда каждому достанется по одной пицце:
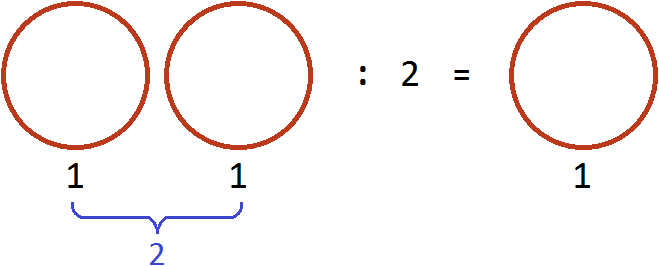
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь

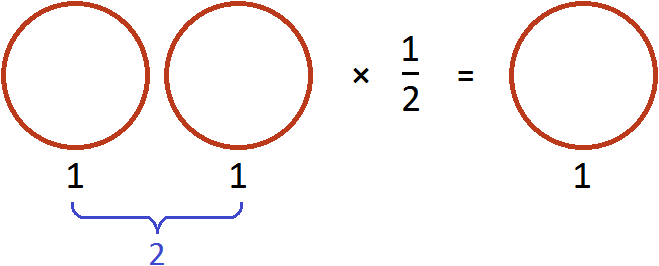
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить
 на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь 
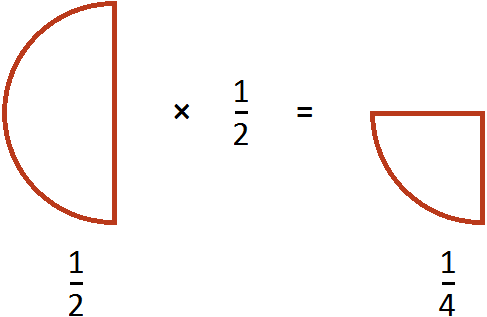
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
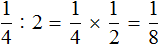
Допустим, у нас имеется четверть пиццы и нужно разделить её на двоих:
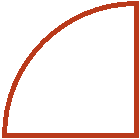
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
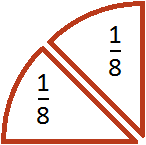
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь

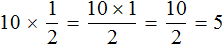
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
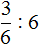
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
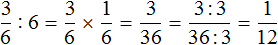
Допустим у нас имелось
 пиццы:
пиццы:Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
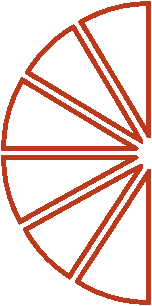
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет
 . Поэтому при делении
. Поэтому при делении  на 6 получается
на 6 получается 
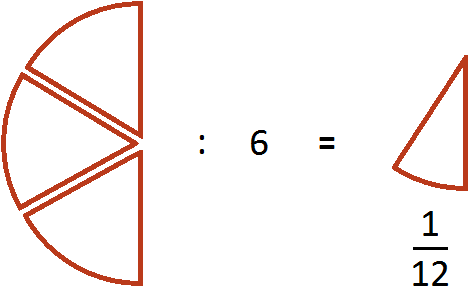
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на
 .
.Чтобы разделить число 1 на
 , нужно это число 1 умножить на дробь, обратную дроби
, нужно это число 1 умножить на дробь, обратную дроби  . А обратная дроби
. А обратная дроби  это дробь
это дробь 
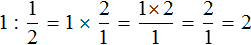
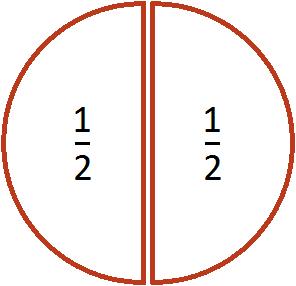
Выражение
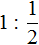 можно понимать, как определение количества половин в одной целой пицце. Допустим у нас имеется одна целая пицца:
можно понимать, как определение количества половин в одной целой пицце. Допустим у нас имеется одна целая пицца:Если зададим вопрос сколько раз половина содержится в этой пицце, то ответом будет 2. Действительно, если мы разделим её пополам, то увидим, что половина содержится в ней два раза
Пример 2. Найти значение выражение
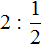
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь

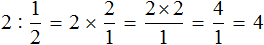
Допустим, у нас имеется две целые пиццы:
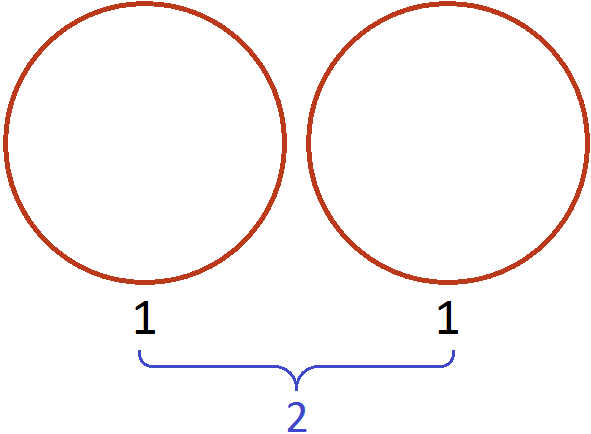
Если зададим вопрос сколько раз половина содержится в этих пиццах, то ответом будет 4. Действительно, если мы разделим эти пиццы пополам, то увидим, что половина содержится в них четыре раза:
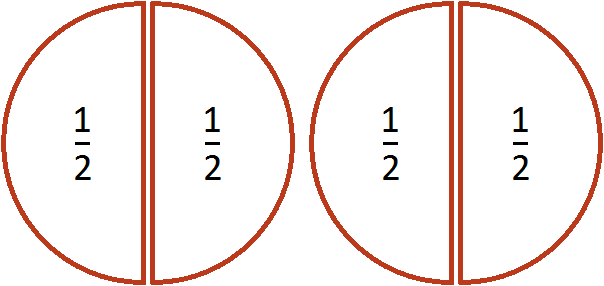
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим
 на
на 
Чтобы разделить
 на
на  , нужно
, нужно  умножить на дробь, обратную дроби
умножить на дробь, обратную дроби  . А обратная дроби
. А обратная дроби  это дробь
это дробь 
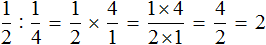
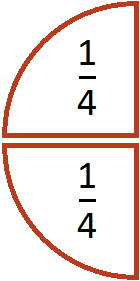
Допустим у нас имеется половина пиццы:

Если зададим вопрос сколько раз четверть пиццы содержится в этой половине, то ответом будет 2. Действительно, если мы разделим её на две части, то увидим, что четверть содержится в ней два раза:
Пример 1. Найти значение выражения
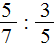
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
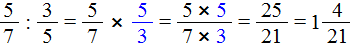
Пример 2. Найти значение выражения
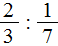
Умножаем первую дробь на дробь обратную второй:
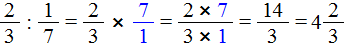
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому желательно тренироваться.
spacemath.xyz
- обратным числа 4 является дробь