Переместительное свойство умножение

Переместительное свойство умножения — полезное правило, не сложное для запоминания.

Переместительное свойство умножения (переместительный закон умножения).

От перестановки мест множителей произведение не изменяется.

С помощью букв переместительное свойство умножения записывают так:

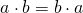
Переместительное свойство умножения позволяет выбирать более удобный способ умножения чисел.

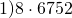
При умножении 8 на 6752

Применяя переместительное свойство умножения,

изменим порядок умножения.

Умножать 6752 гораздо удобнее.

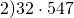
Как правило, умножать трехзначное

число на двухзначное

удобнее, чем наоборот.

Умножать числа в том порядке,

как они записаны в условии,

здесь не так удобно.

Таким образом, применение переместительного свойства умножения позволяет облегчить вычисления.

www.for6cl.uznateshe.ru

Запиши на математическом языке:
переместительное свойство сложения и умножения:
сочетательное свойство сложения и умножения:
распредилительное свойство умножения:
правило деление суммы на число:
правило вычитания числа из суммы:
правило вычитания суммы из числа
Объясни их смысл,Заранее спасибо

Ответы и объяснения

1 Переместительный закон сложения и умножения:
От перемены мест слагаемых сумма не меняется.(Значение суммы при перестановке двух слагаемых не меняется.)a + b = b + a = с
От перемены мест множителей произведение не меняется.(Значение произведения при перестановке множителей не меняется.)a x b = b x a = с
2 Сочетательное свойство сложения и умножения:Для любых чисел a, b и c верны равенства: (a + b) + c = a + (b + c) и (ab)c = a(bc)

3 Распределительное свойство умножения:Для любых чисел a, b и c верны равенства: (a + b) + c = a + (b + c) и (ab)c = a(bc)
Из переместительного и сочетательного свойств сложения следует, что в любой сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.
Точно также из переместительного и сочетательного свойств умножения следует, что в любом произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.
Распределительное свойство справедливо и в том случае, когда число умножается на сумму трех и более слагаемых.
Для любых чисел a, b, c и d, верно равенство: a(b + c + d) = ab + ac + ad

4 правило деления суммы на число:
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и полученные результаты сложить: (а + b) : с = а : с + b : с

5 Правило вычитания числа из суммы: 1. Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое, а из полученного результата (разности) вычесть второе слагаемое. Например: 126 — (56 + 30) = (126 — 56) — 30 = 40. В общем виде: а — (Ь + с) = (а — Ь) — с. Правило 2. Чтобы вычесть число из суммы, можно вычесть его из одного из слагаемых и к результату прибавить второе слагаемое. Правило 2 можно использовать при вычислении натуральных чисел только в случае, если одно из слагаемых больше вычитаемого числа. Например: (71 + 7) — 51 = (71 — 51) + 7 = 20 + 7 = 27, но нельзя (71 + 7) — 51 = (7 — 51) + 71,так как разность (7 — 51) — ненатуральное число. В общем виде: (а + Ь) — с = (а — с) + Ь.
6 правило вычитание суммы из числа
а-(х+у) = а-х-у. Если перед скобкой стоит знак «-«, то знаки в скобке меняются на противоположный

znanija.com

Переместительное свойство сложения

На данном уроке мы рассмотрим переместительное свойство сложения, используя при этом разные геометрические фигурки. Также вы научитесь использовать его для упрощения вычислений в различных жизненных ситуациях. У вас будет возможность вспомнить, как называются числа при сложении.

Решение задачи с кружками

На рисунке слева изображены два желтых кружка, справа – один белый.

Найдем, сколько всего кружков изображено. Для этого к двум желтым кружкам прибавим один белый.

2 + 1 = 3

Получаем три кружка.

Далее поменяем кружки местами. Белый кружок переместим и поставим слева, а два желтых будут справа. Изменилось ли количество кружков?

Запишем, какое действие необходимо выполнить. Для этого к одному белому прибавим два желтых.

1 + 2 = 3

Видим, что количество кружков осталось то же.

Решение задачи с квадратами

Такое же действие проделаем с квадратами. К трем розовым квадратам прибавим два зеленых и запишем действие, которое получилось.

3 + 2 = 5

Получилось 5 квадратов.

Теперь поменяем местами зеленые и розовые квадраты. К двум зеленым добавим три розовых квадрата.

2 + 3 = 5

Количество квадратов не изменилось. Их пять.

Действие сложения, числа при сложении

Вспомним, какое действие мы все время выполняли. Выполняли действие сложения. Теперь вспомним, что числа при сложении называются слагаемыми и значением суммы.

Формулировка переместительного свойства сложения

Что мы проделывали с кругами и с квадратами? Мы их меняли местами. И доказывали, что при перестановке слагаемых значение суммы не изменяется. В математике это называется переместительным свойством сложения.

Пример применения переместительного свойства сложения

На рисунке изображены два столбика примеров. Необходимо найти суммы в левом и правом столбике с одинаковым значением, соединив их стрелочками.

2+5

2+7

8+3

5+2

7+2

3+8

То есть, не нужно выполнять вычисления, чтобы найти суммы с одинаковым значением, поскольку можно воспользоваться переместительным свойством сложения.

Мы знаем, что переместительное свойство сложения – это когда слагаемые меняются местами.

2 + 5 = 7 5 + 2 = 7

От перестановки слагаемых сумма не меняется.

Решение равенств путем применения переместительного свойства сложения

Необходимо дописать равенства, воспользовавшись переместительным свойством слагаемых.

1 + 2 = 2 +…

8 + 2 = …+…

6 + 4 = …+…

7 + 3 = 4 + 6

Для этого достаточно поменять слагаемые местами.

1 + 2 = 2 + 1

8 + 2 = 2 + 8

6 + 4 = 4 + 6

Тут мы воспользовались переместительным свойством сложения. Теперь подумайте, подойдет ли равенство 7 + 3 = 4 + 6 к нашему заданию?

Правильный ответ: нет. Хотя изначально значение сумм одинаковое (7 + 3 = 10 и 4 + 6 = 10) и равенство верное, но здесь не было выполнено перестановки слагаемых, то есть тут мы не пользовались переместительным свойством сложения.

Итак, на данном уроке мы изучили переместительное свойство сложения, которое заключается в том, что от перестановки слагаемых значение суммы не изменяется. Также мы повторили, как называются числа при сложении.

Список литературы

• Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
• Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
• Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Законы арифметики (Источник).
2. Фестиваль педагогических наук «Открытый урок» (Источник).
3. Infourok.ru (Источник).

Домашнее задание

Какое основное правило переместительного свойства сложения?

Запишите выражения, пользуясь переместительным свойством сложения:

Как называются числа при сложении?

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

interneturok.ru

Урок математики по теме «Переместительное свойство сложения»

Цели:

• познакомить с переместительным свойством сложения;
• закрепить состав чисел 2, 3, 4, 6;
• закреплять умение составлять равенства по числовому лучу;

Оборудование:

• карточки с составом чисел;
• карточки – вагончики с выражениями;
• карточки с фишками домино;
• карточки – шарики с выражениями;
• учебник Н.Б. Истоминой “Математика” 1 класс.
• Организационный момент.
• Повторение изученного.

1. Устный счёт.

• Состав каких чисел уже знаем?
• Проверим, как вы выучили его.

(учитель показывает классу карточки состава чисел с “окошками”, а учащиеся на “веере” чисел демонстрируют число, которое надо вставить в “окошко”)

— А теперь мы с вами отправимся в путешествие за математическими знаниями.

— Поедем на волшебном поезде.

(открывается доска, на которой прикреплены вагоны с выражениями)

— Но прежде, чем отправимся в путь, надо узнать, сколько пассажиров едет в каждом вагоне. Что для этого надо сделать?

(найти значения выражений)

(учащиеся показывают результаты на “веере” с числами)

1. Постановка проблемы.

— Сегодня на уроке нам предстоит открыть один очень нужный математический закон. Вы готовы к его открытию?

2. Знакомство с законом.

— Кто из вас знает такую игру – домино? А как в неё играть?

(объяснение правил игры: фишки присоединяются друг к другу одинаковым количеством кружков)

— С правилами игры разобрались. А теперь давайте попробуем выяснить, какое существует правило в расположении фишек домино у меня на доске?

(на доске рисунок из учебника № 161)

— Кто может нам объяснить как, по какому правилу, разбили фишки на группы?

(коллективный разбор: общее число кружков, кружки поменяли местами)

— Давайте составим с вами равенства, чтобы увидеть общее количество кружков на каждой фишке.

а) работа в тетрадях

(учащиеся записывают в тетрадях равенства, а потом учитель выносит эти равенства на доску:

2 + 4 = 6 6 + 1 = 7 5 + 3 = 8

4 + 2 = 6 1 + 6 = 7 3 + 5 = 8)

• Посмотрите на полученные столбики равенств. Что же общего в записях каждой пары равенств?

(суммы, слагаемые, верные равенства)

• Можете ли вы назвать различия в записи сумм каждой пары равенств?

(числа поменялись местами)

— А как при сложении называются числа?

— Значит, слагаемые (поменяли) переставили, но значение суммы не изменилось.

— Хорошо. Действие сложение мы умеем выполнять не только с группами предметов, но и при движении по числовому лучу.

б) работа по учебнику

(учащиеся открывают учебник на стр. 74, № 162)

— Надо записать равенства, соответствующие рисункам, и проверить, подтвердится ли наш вывод здесь.

(работа в парах: учащиеся в учебнике подписывают карандашом равенства над лучами)

— Какие равенства получили?

— Что можем сказать о полученных равенствах?

(значения одинаковые, числа поменялись местами)

— Могу сообщить вам, что это свойство действия сложения. Оно будет проявляться при любых значениях слагаемых. И называется это свойство сложения – ПЕРЕМЕСТИТЕЛЬНОЕ.

(на доску прикрепляется карточка с названием свойства сложения)

— И звучит оно так: от перестановки слагаемых значение суммы не меняется.

— Найдём это правило в учебнике и прочитаем его.

(вначале учащиеся читают его самостоятельно, а потом все вместе)

Теперь мы с вами знаем переместительное свойство сложения. Зачем оно нам нужно, мы узнаем на следующих уроках.

— А нам пора возвращаться на нашем поезде. Давайте украсим наш поезд шариками, чтобы было видно, что мы сегодня на уроке открыли закон сложения.

б) работа по карточкам

— У вас у каждого на столе находится карточка с шариками. Соедините шарики парами, используя наше открытие.

(учащиеся соединяют шарики, используя переместительное свойство сложения)

— Проверим, какие пары шариков у вас получились и прикрепим эти пары на наши вагоны.

(учащиеся выходят к доске и выбирают пары шариков, прикрепляют их к вагонам)

1. Итог урока.

   — Молодцы! Наш поезд успешно вернулся из путешествия.

   — Какое открытие мы сегодня сделали на уроке?

   — Запомните это свойство сложения и расскажите о нём дома родителям.

   xn--i1abbnckbmcl9fb.xn--p1ai

   Свойства сложения, умножения, вычитания и деления целых чисел.

   Мы определили сложение, умножение, вычитание и деление целых чисел. Эти действия (операции) обладают рядом характерных результатов, которые называются свойствами. В этой статье мы рассмотрим основные свойства сложения и умножения целых чисел, из которых следуют все остальные свойства этих действий, а также свойства вычитания и деления целых чисел.

   Навигация по странице.

   Основные свойства сложения целых чисел

   Для начала нужно сказать, что все свойства сложения натуральных чисел справедливы для сложения целых чисел. Это обусловлено тем, что натуральные числа являются составной частью целых чисел. Перечислим основные свойства сложения.

   Во-первых, сложение целых чисел обладает переместительным свойством. Это свойство заключается в том, что результат сложения двух целых чисел не зависит от порядка следования слагаемых. То есть, для двух целых чисел a и b справедливо равенство a+b=b+a . К примеру, в силу рассмотренного свойства справедливо равенство 3+21=21+3 ; также справедливо равенство (−564)+45=45+(−564) ; сумма целых отрицательных чисел −2 и −6 754 равна сумме (−6 754)+(−2) .

   Во-вторых, сложение целых чисел обладает сочетательным свойством. Сочетательное свойство заключается в том, что результат сложения целого числа с суммой двух целых чисел равен результату сложения суммы двух первых целых чисел с третьим. Это свойство сложения проще усвоить, когда оно записано в буквенном виде: a+(b+c)=(a+b)+c , где a , b , c – произвольные целые числа. Приведем пару примеров. Рассмотренное свойство сложения целых чисел позволяет говорить о справедливости равенства 54+((−17)+(−3 400))=(54+(−17))+(−3 400) ; аналогично сумма вида 10+((−100)+1 000) равна сумме (10+(−100))+1 000 .

   Следует заметить, что значение сочетательного свойства сложения целых чисел состоит еще и в том, что оно позволяет однозначно определить сложение трех, четырех и большего количества целых чисел.

   Для сложения целых чисел характерны еще несколько очень важных свойств.

   Одно из них связано с существованием нуля. Это свойство сложения целых чисел утверждает, что прибавление к любому целому числу нуля не изменяет это число. Запишем данное свойство сложения с помощью букв: a+0=a и 0+a=a (это равенство справедливо в силу переместительного свойства сложения), a – любое целое число. Можно услышать, что целое число нуль называют нейтральным элементом по сложению. Приведем пару примеров. Сумма целого числа −78 и нуля равна −78 ; если к нулю прибавить целое положительное число 999 , то в результате получим число 999 .

   Сейчас мы дадим формулировку еще одного свойства сложения целых чисел, которое связано с существованием противоположного числа для любого целого числа. Сумма любого целого числа с противоположным ему числом равна нулю. Приведем буквенную форму записи этого свойства: a+(−a)=0 , где a и −a – противоположные целые числа. Например, сумма 901+(−901) равна нулю; аналогично сумма противоположных целых чисел −97 и 97 равна нулю.

   Основные свойства умножения целых чисел

   Умножению целых чисел присущи все свойства умножения натуральных чисел. Перечислим основные из этих свойств.

   Умножение целых чисел обладает переместительным свойством. Оно утверждает, что результат умножения двух целых чисел не зависит от порядка следования множителей. То есть, для любых целых чисел a и b справедливо равенство a·b=b·a . Например, произведение целых чисел 56 и −9 равно произведению чисел −9 и 56 ; также справедливо равенство (−678)·(−92)=(−92)·(−678) .

   Для умножения целых чисел характерно сочетательное свойство. В буквенном виде оно записывается так: a·(b·c)=(a·b)·c , где a , b , c – произвольные целые числа. Приведем пример. В силу переместительного свойства умножения целых чисел можно говорить о справедливости равенства (−12)·(56·90 003)=((−12)·56)·90 003 .

   Сочетательное свойство умножения целых чисел позволяет определить умножение трех и большего количества целых чисел.

   Также как нуль является нейтральным целым числом относительно сложения, единица является нейтральным целым числом относительно умножения целых чисел. То есть, умножение любого целого числа на единицу не изменяет умножаемое число. Так 1·a=a , где a – любое целое число. Последнее равенство можно переписать в виде a·1=a , это нам позволяет сделать переместительное свойство умножения. Приведем два примера. Произведение целого числа 556 на 1 равно 556 ; произведение единицы и целого отрицательного числа −78 равно −78 .

   Следующее свойство умножения целых чисел связано с умножением на нуль. Результат умножения любого целого числа a на нуль равен нулю, то есть, a·0=0 . Также справедливо равенство 0·a=0 в силу переместительного свойства умножения целых чисел. В частном случае при a=0 произведение нуля на нуль равно нулю.

   Для умножения целых чисел также справедливо свойство, обратное к предыдущему. Оно утверждает, что произведение двух целых чисел равно нулю, если хотя бы один из множителей равен нулю. В буквенном виде это свойство можно записать так: a·b=0 , если либо a=0 , либо b=0 , либо и a и b равны нулю одновременно.

   Распределительное свойство умножения целых чисел относительно сложения

   Совместно сложение и умножение целых чисел нам позволяет рассматривать распределительное свойство умножения относительно сложения, которое связывает два указанных действия. Использование сложения и умножения совместно открывает дополнительные возможности, которых мы были бы лишены, рассматривая сложение отдельно от умножения.

   Итак, распределительное свойство умножения относительно сложения гласит, что произведение целого числа a на сумму двух целых чисел a и b равно сумме произведений a·b и a·c , то есть, a·(b+c)=a·b+a·c . Это же свойство можно записать в другом виде: (a+b)·c=a·c+b·c .

   Распределительное свойство умножения целых чисел относительно сложения вместе с сочетательным свойством сложения позволяют определить умножение целого числа на сумму трех и большего количества целых чисел, а далее – и умножение суммы целых чисел на сумму.

   Также заметим, что все остальные свойства сложения и умножения целых чисел могут быть получены из указанных нами свойств, то есть, они являются следствиями указанных выше свойств.

   Свойства вычитания целых чисел

   Мы знаем, что вычитание целых чисел является действием, обратным к сложению целых чисел. Вычитание – это действие, при котором находится неизвестное слагаемое по известной сумме и известному слагаемому (об этом мы говорили в разделе теории смысл вычитания целых чисел). То есть, целое число c является разностью целых чисел a и b , когда сумма b+c равна a .

   Такое определение разности, а также свойства сложения целых чисел, позволили нам доказать, что разность целых чисел a и b равна сумме числа a и числа −b , противоположного b . То есть, a−b=a+(−b) (доказательство этого равенства приведено в разделе теории правило вычитания целых чисел).

   Из полученного равенства, а также из свойств сложения и умножения целых чисел вытекают следующие свойства вычитания целых чисел ( a , b и c – произвольные целые числа):

2. Вычитание целых чисел в общем случае НЕ обладает переместительным свойством: a−b≠b−a .
3. Разность равных целых чисел равна нулю: a−a=0 .
4. Свойство вычитания суммы двух целых чисел из данного целого числа: a−(b+c)=(a−b)−c .
5. Свойство вычитания целого числа из суммы двух целых чисел: (a+b)−c=(a−c)+b=a+(b−c) .
6. Распределительное свойство умножения относительно вычитания: a·(b−c)=a·b−a·c и (a−b)·c=a·c−b·c .
7. И все другие свойства вычитания целых чисел.

Свойства деления целых чисел

Рассуждая о смысле деления целых чисел, мы выяснили, что деление целых чисел – это действие, обратное умножению. Мы дали такое определение: деление целых чисел – это нахождение неизвестного множителя по известному произведению и известному множителю. То есть, целое число c мы называем частным от деления целого числа a на целое число b , когда произведение c·b равно a .

Данное определение, а также все рассмотренные выше свойства операций над целыми числами позволяют установить справедливость следующих свойств деления целых чисел:

• Никакое целое число нельзя делить на нуль.
• Свойство деления нуля на произвольное целое число a , отличное от нуля: 0:a=0 .
• Свойство деления равных целых чисел: a:a=1 , где a – любое целое число, отличное от нуля.
• Свойство деления произвольного целого числа a на единицу: a:1=a .
• В общем случае деление целых чисел НЕ обладает переместительным свойством: a:b≠b:a .
• Свойства деления суммы и разности двух целых чисел на целое число: (a+b):c=a:c+b:c и (a−b):c=a:c−b:c , где a , b , и c такие целые числа, что и a и b делится на c , и c отлично от нуля.
• Свойство деления произведения двух целых чисел a и b на целое число c , отличное от нуля: (a·b):c=(a:c)·b , если a делится на c ; (a·b):c=a·(b:c) , если b делится на c ; (a·b):c=(a:c)·b=a·(b:c) , если и a и b делятся на c .
• Свойство деления целого числа a на произведение двух целых чисел b и c (числа a , b и c такие, что деление a на b·c возможно): a:(b·c)=(a:b)·c=(a:c)·b .
• Любые другие свойства деления целых чисел.

www.cleverstudents.ru