17. Прямоугольный параллелепипед. Объем. Правила

На рисунке изображен прямоугольный параллелепипед. В жизни мы сталкиваемся с такой формой в виде коробка спичек, коробки из-под обуви, кирпича и т.д.
Прямоугольники, составляющие поверхность параллелепипеда, называются гранями. У параллелепипеда их 6, причем грани расположенные напротив друг друга равны. У параллелепипеда есть 12 ребер, они также являются сторонами граней. Точки схождения ребер называются вершинами параллелепипеда. Площадь грани 1 изображенной на рисунке равна произведению первого и второго ребра.
Площадь всей поверхности параллелепипеда равна сумме площадей граней 1, 2 и 3 умноженной на 2.
Прямоугольный параллелепипед определяется тремя измерениями.
Высота (обозначим буквой h) равна длине ребра № 1.
Длина (обозначим буквой m) равна длине ребра № 2.
Ширина (обозначим буквой n) равна длине ребра № 3.
Если площадь всей поверхности параллелепипеда обозначить буквой S, то формула ее нахождения будет выглядеть так:
S = (h • m + h • n + n • m) • 2
 Кубом называют прямоугольный параллелепипед, у которого все измерения равны. Поверхность куба составляет 6 равных квадратов.
Кубом называют прямоугольный параллелепипед, у которого все измерения равны. Поверхность куба составляет 6 равных квадратов.
Если длину ребра куба обозначить буквой n, то площадь одной грани S = n 2
Прямоугольный параллелепипед обладает еще одним измерением, которое называется объем (обозначим буквой V) .
V = h • m • n
Величина объем показывает, какую часть пространства занимает объект. В быту объем чаще всего используется для измерения жидкостей, и самая распространенная единица измерения объема является литр = 1дм 3 .
Так же для измерения объема используются м 3 , мм 3 , см 3 , км 3 .
Куб с размерами 1см будет обладать объемом 1 см 3 .
V = 1 см • 1 см • 1 см = 1 см 3 .
Два таких куба вместе займут вдвое больший объем 2 см 3 , то есть объем объекта это сумма объемов фигур, из которых состоит объект.
Задачи на тему «Прямоугольный параллелепипед. Объем»
Найди неизвестную величину, используя формулы объема прямоугольного параллелепипеда V = abc.
1) a = 9 м 2) b = 4 см 3) а = 30 см
b = 12 м с = 13 см с = 17 дм
с = 5 м V = 104 с м 3 V = 102 д м 3
V = м 3 a = см b = дм
Найди неизвестную величину, используя формулу объема прямоугольного параллелелепипеда V = S h.
1) S = 30 д м 2 2) V = 45 м 3 3) h = 80 cм
h = 5 дм h = 9 м S = 40 д м 2
school-assistant.ru
Многогранники и Объем многогранников
Многоугольники относятся к плоским геометрическим фигурам. К объемным (трехмерным) геометрическим фигурам относятся многогранники.
Определение. Многогранник — это геометрическое пространственное тело, ограниченное со всех сторон конечным числом плоских многоугольников (граней).
Прямоугольный параллелепипед является многогранником. Простейший прямоугольный параллелепипед — это куб. У него все грани равны
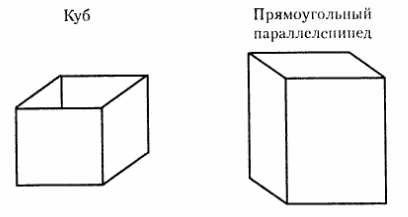
У прямоугольного параллелепипеда каждая грань — прямоугольник, который имеет с соседней гранью общую сторону и две общие вершины.
У параллелепипеда 8 вершин, 4 боковых прямоугольника и 2 прямоугольника в основаниях. У куба все б граней — равные квадраты. У прямоугольного параллелепипеда боковые фигуры и основания — прямоугольники. Эти прямоугольники попарно равны (равны прямоугольники оснований и две пары противолежащих прямоугольников, составляющих боковые грани). Следовательно, грани прямоугольного параллелепипеда являются прямоугольниками трех типов, различающихся размерами.
Три прямоугольника с разными размерами имеют
одну общую точку — вершину параллелепипеда.
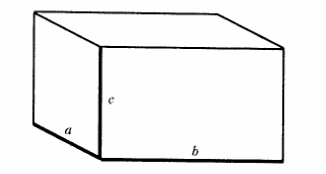
У каждой вершины параллелепипед имеет общую точку для трех отрезков, которые называются измерениями параллелепипеда (длина, ширина и высота). Три измерения на верхнем рисунке параллелепипеда выделены жирной линией.
Объем — это то количество жидкости или сыпучего материала, которое можно поместить внутрь фигуры (между граничными плоскостями).
Объем — это одна из характеристик трехмерных геометрических фигур.
Объем обозначается большой латинской буквой V («вэ»). Величины объема взаимосвязаны (одну кубическую единицу объема можно заменить ругой).
Правило. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Единицами измерения объема служат:
-
а) стандартные единицы длины в кубе:
1 см 3 = 1 000 мм 3
1 дм 3 = 1 000 см 3 = 1 000 000 мм 3
1 м 3 = 1 000 дм 3 = 1 000 000 см 3 — 1 000 000 000 мм 3
1 км 3 — 1 000 000 000 м 3
- б) специальная единица объема (литр):
1 л = 1 дм 3 = 1 000 см 3 .
Формула для расчета объема прямоугольного параллелепипеда:
где а — длина, Ь — ширина, с — высота.
Так как у куба все измерения равны (а = Ь = с), то формула для вычисления объема куба V = а 3 .
Вычислить объем прямоугольного параллелепипеда длиной 6 м, шириной 4 м и высотой 8 м.
Решение. Так как длина, ширина и высота измеряются одной и той же единицей длины (м), то подставим их в формулу V=а*Ь*с и вычислим объем:
V = 6 * 4 * 8 = 192 (м 3 )
Ответ: 192 м 3 .
Вычислите объем куба со стороной основания 10 см.
Решение. Подставим численное значение стороны куба в формулу вычисления объема V=а 3 и вычислим:
V = 10 * 10 * 10 = 10 3 = 1 000 (см 3 ) — 1 л.
shkolo.ru
Найти объем прямоугольного параллелепипеда
Параллелепипед – это призма, основанием которой служит параллелограмм.
В параллелепипеде противоположные грани равны и параллельны.
Диагонали его пересекаются в одной точке, которая лежит на оси симметрий, и делятся ею пополам.
Объём параллелепипеда равен произведению его измерений.
Формула для вычисления объема параллелепипеда:
$$V = a \cdot b \cdot c$$
- Найдите объем прямоугольного параллелепипеда, если его стороны равны 2,3,4 см.
Посмотреть решение
Решение:
По формуле для объема прямоугольного параллелепипеда:
$$ V = 2 \cdot 3 \cdot 4 = 24 \ см^3 $$
$$ V = So \cdot c =a \cdot b \cdot c $$
$$ V = 7 \cdot 4 = 28 \ см^3 $$
Ответ:
Найдем третью сторону:
$$ Sбок = 2 \cdot c \cdot (a+b) $$
$$ V = a \cdot b \cdot c $$
$$ V = 1 \cdot 3 \cdot 2 = 6 \ см^3 $$
Найдем площадь основания прямоугольного параллелепипеда:
$$ Sо = S — Sбок = 9 см^2 $$
$$ V = So \cdot c = a \cdot b \cdot c $$
$$ V = 9 \cdot 5 = 45 \ см^3 $$
Все стороны равны — значит это куб. По формуле для объема прямоугольного параллелепипеда:
algebra24.ru
Объем прямоугольного параллелепипеда правило

Прямоугольный параллелепипед — это пространственная фигура, ограниченная прямоугольниками.
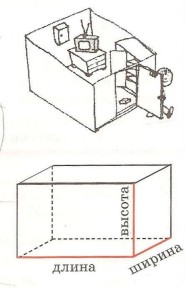
Форму параллелепипеда имеют многие предметы из окружающей обстановки: коробка, кубики, телевизор, шкаф и т. д..
Поверхность параллелепипеда состоит из 6 прямоугольников, которые называют гранями. Противоположные грани параллелепипеда равны.
Вершины граней называют вершинами параллелепипеда, а стороны граней — рёбрами. У параллелепипеда 8 вершин и 12 рёбер. Но разную длину могут иметь лишь 3 ребра. Их называют измерениями параллелепипеда — длиной, шириной и высотой.
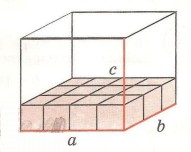
Остальные ребра равны длине, ширине и высоте как противоположные стороны прямоугольников.
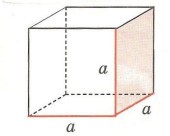
Некоторые измерения параллелепипеда могут быть равны между собой. Если равны все три измерения, то параллелепипед называется кубом. У куба все грани являются квадратами, а все рёбра равны между собой.
Если стороны основания параллелепипеда равны а и b, то на это основание можно выставить а • b единичных кубиков. Так как в высоту выкладывается с таких слоев, то объём V параллелепипеда вычисляется по формуле:
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Найти объём прямоугольного параллелепипеда с измерениями б см, 9 см, 2 см.
Решение: б • 9 • 2 = 108 (см 2 ).
Замечание. Формулу V = a • b • c можно читать разными способами.
1. Если нужно напомнить правило, тогда говорят так: «Объём вэ прямоугольного параллелепипеда равен произведению трёх его измерений а, бэ и цэ».
2. Если нужно только прочитать запись формулы, то говорят: «Вэ равно произведению а, бэ и цэ». Название единиц объёма читают полностью, например: 108 см 3 — сто восемь кубических сантиметров.
1. На модели прямоугольного параллелепипеда покажи грани, рёбра, вершины. Сколько граней, рёбер и вершин имеет прямоугольный параллелепипед?
2. По рисунку параллелепипеда назови:
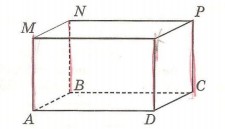
а) верхнюю и правую грани;
б) рёбра, равные ребру AM (обведи их красным карандашом);
в) вершины, принадлежаш;ие задней грани;
г) грань, равную ABCD.
3. Каркас параллелепипеда сделан из проволоки. Его размеры указаны на рисунке. Сколько проволоки для него потребовалось?
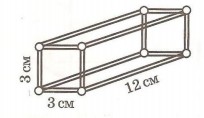
4. Напиши формулу объёма прямоугольного параллелепипеда. Найди объём параллелепипеда, если:
а) а = 8 см, b = 10 см, с = 9 см;
б) а = 30 м, b = 20 м, с = 70 м;
в) а = 2 дм, b = 70 см, с = 50 см.
(Обрати внимание на единицы измерения!)
5. Напиши формулу объёма куба со стороной а . Найди объём куба, если:
1) а = 4 см; 2) а = 60 м; 3) а = 900 см.
6. Высота комнаты 3 м, ширина 4 м, а длина 7 м. Сколько кубических метров воздуха находится в комнате? Чему равна плопдадь пола, потолка, стен?
7. а) Найди сумму площадей всех граней параллелепипеда, если его измерения равны 5 см, 2 см и 3 см.
б) Напиши формулу площади поверхности параллелепипеда с измерениями а, b и с.
в) Напиши формулу площади поверхности куба со стороной а.
8. Реши уравнения с комментированием и сделай проверку:
а) 35 : у + б — 11; г) (m : 5 + 3) • 6 = 48;
б) 50 — 9 • а = 23; д) (9 • t — 14) : 4 = 10;
в) (4 + х): 8 = 9; е) 56 : (36 : k — 2) = 8.
9. Игорь решил примеры на деление с остатком и записал их так:
53 : 7 = 6 (ост. 11)
Правильно ли он выполнил вычисления? Обоснуй свой ответ.
10. Выполни деление с остатком и сделай проверку:
а) 81 580 : 9; б) 672 043 : в) 402 600 : 50; г) 3 582 270 : 60.
11. Прочитай числа:
75 994 608, 75 994 600 315, 70 000 031, 712 021, 99 999.
Расположи эти числа в порядке возрастания.
12*. Какой из кубиков, изображённых на рисунке, точно такой же, как кубик М?
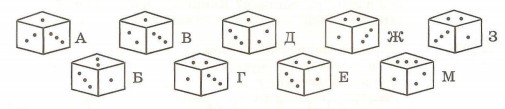
Решение можно проверить на модели куба.
Петерсон Людмила Георгиевна. Математика. 3 класс. Часть 2. — М.: Издательство «Ювента», 2005, — 64 с.: ил.
Математика скачать, задача школьнику 3 класса, материалы по математике для 3 класса онлайн
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
edufuture.biz
21. Объёмы. Объём прямоугольного параллелепипеда
Если наполнять формочку влажным песком, а потом переворачивать и снимать её, получатся фигуры, имеющие одинаковый объём (рис. 83). Если формочку наполнять водой, то объём воды будет равен объёму каждой фигуры из песка.

Чтобы сравнить объёмы двух сосудов, можно наполнить один из них водой и перелить её во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объёмы сосудов равны. Если в первом сосуде вода останется, то его объём больше объёма второго сосуда. А если заполнить водой второй сосуд не удастся, то объём первого сосуда меньше объёма второго.

Для измерения объёмов применяют следующие единицы: кубический миллиметр (мм 3 ), кубический сантиметр (см 3 ), кубический дециметр (дм 3 ), кубический метр (м 3 ), кубический километр (км 3 ).
Например: кубический сантиметр — это объём куба с ребром 1 см (рис. 84).

Кубический дециметр называют также литром. 1 л = 1 дм 3
Фигура на рисунке 85 состоит из 4 кубиков с ребром 1 см. Значит, её объём равен 4 см 3 .
Выведем правило для вычисления объёма прямоугольного лараллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см (рис. 86, а). Разобьём его на два слоя толщиной 1 см



(рис. 86, б). Каждый из этих слоёв состоит из 3 столбиков длиной 4 см (рис. 86, в), а каждый столбик — из 4 кубиков с ребром 1 см. (рис. 86, г). Значит, объём каждого столбика равен 4 см 3 , каждого слоя — 4 • 3 ( см 3 ), а всего прямоугольного параллелепипеда — (4 • 3) • 2, то есть 24 см 3 .

Чтобы найти объём прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.
Формула объёма прямоугольного параллелепипеда имеет вид
V = abc.
где V — объём; а, b, с — измерения.
Если ребро куба равно 4 см, то объём куба равен 4 • 4 • 4 = 4 3 (см 3 ), то есть 64 см 3 .
Если ребро куба равно а, то объём V куба равен a • a • a = a 3
Значит, формула объёма куба имеет вид
V = а 3 .
Именно поэтому запись а 3 называют кубом числа а.

Объём куба с ребром 1 м равен 1 м 3 . А так как 1 м = 10 дм, то 1 м 3 = 103 дм 3 , то есть 1 м 3 = 1000 дм 3 = 1000 л. Таким же образом находим, что
1 л = 1 дм 3 = 1000 см 3 ; 1 см 3 = 1000 мм 3 ;
1 км 3 = 1 000 000 000 м 3 (см. форзац).
www.xn--24-6kct3an.xn--p1ai
