Закон Ома для участка цепи
Закон Ома для участка цепи — это основной закон в электротехнике. Он устанавливает связь между током, сопротивлением и напряжением. С его помощью можно изучить и рассчитать электрические цепи. Важно не просто выучить закон Ома, а понять его, как он применяется на самом деле. Так как довольно часто происходят ошибки в его применении на практике, из-за не правильного его использования.
Закон Ома определение — ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Стоит поднять напряжение, проходящее по электро цепи, ток так же поднимется догнав напряжение. Подняв сопротивление в цепи, ток снизится во столько же раз, во сколько поднялось сопротивление. Это можно увидеть на простом примере, взять простую трубу и пустить через нее поток воды, чем выше давление тем сильнее поток воды, если же встречается сопротивление то поток воды значительно теряет свою скорость.
В математике принято считать: сопротивление проводника, в котором во время напряжения 1В протекает ток 1А — равняется 1Ом.
Закон Ома формула — расшифровывается как определение тока в амперах с помощью деления напряжения на сопротивление в омах.
I=U/R
Правильные вычисления по закону Ома будут только тогда , когда напряжение отражается в вольтах, сопротивление в Омах, ток в амперах. При использовании различных версий данных величин, следует их преобразовывать в нужные для вычисления величины.
Данный закон одинаков для всего участка цепи. В случае выяснения напряжения на конкретном участке, нужно будет брать размеры всех величин именно с этого участка.
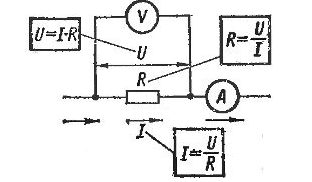
Данный закон можно рассмотреть на примерах:
1)Определим ток в лампе с сопротивлением 2,5ОМ и напряжении 5В. Разделим 5 / 2,5 получим ток = 2А
Когда ток и сопротивление известны, напряжение так же находят с помощью закона Ома. С помощью формулы:
U = IR
Из чего мы видим, напряжение в концах участка цепи ровно пропорционально току и сопротивлению. Так как увеличение тока без изменения сопротивления, возможно только при увеличения напряжения. Следовательно, постоянное сопротивление большему току, преследует большое напряжение. Если использовать постоянно одинаковый ток с разным сопротивлением, с большим сопротивлением нужно большее напряжение.
Вычисление напряжения можно рассмотреть на примере:
Вычислить напряжение с током = 5мАм (0,005А), сопротивление 10кОм (10000 Ом). Умножаем ток * напряжение = 50В.
Связь между током и напряжением называется — сопротивление. Увеличивается напряжение так же происходит и увеличение тока, ровно тоже происходит при уменьшении. Соотношение между напряжением и током = сопротивлению, которое не меняется. При рассмотрении двух участков с одинаковым током и разным напряжением, ясно, что в участке с большим напряжением, большее сопротивление. В случае же когда напряжение одинаково, а ток разный, то на участке где меньшее количество тока будет большее сопротивление.
Вычисление сопротивления можно рассмотреть на примере:
Найти сопротивление, имея напряжение 40В и ток 50мАм (0,05А). Поделим 40/0,05 сопротивление = 800 Ом.
Заметка: Интересуют двухуровневые натяжные потолки SATIN.BY. Перейдите по ссылке натяжной потолок (http://satin.by/natjazhnye-potolki.html) и узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Разделы: Физика
Тип урока: Комбинированный.
Вид урока: Изучение нового материала.
Образовательная: установить зависимость между силой тока, напряжением на однородном участке электрической цепи и сопротивлением этого участка.
Воспитательная: развивать познавательный интерес к предмету, тренировка рационального метода запоминания формул.
Усвоить, что сила тока прямо пропорциональна напряжению на концах проводника, если при этом сопротивление проводника не меняется;
- Усвоить, что сила в участке цепи обратно пропорциональна его сопротивлению, если при этом напряжение остается постоянным;
- Знать закон Ома для участка цепи;
- Уметь определять силу тока; напряжения по графику зависимости между этими величинами и по нему же – сопротивление проводника;
- Уметь наблюдать, сопоставлять, сравнивать и обобщать результаты демонстрационного эксперимента;
- Уметь применять закон Ома для участка цепи при решении задач;
- Отрабатывать навыки проверки размерности;
- Отрабатывать навыки соотношения полученных результатов с реальными значениями величин.
- напряжение, если это источник ЭДС;
- силу тока, если это источник тока;
Демонстрационные амперметр и вольтметр, источник тока В-24, ключ, соединительные провода, демонстрационный магазин сопротивления, ТСО, экран, магнитная доска, магниты, портрет Ома, таблицы с формулами.
1. Организационный момент.
Учитель: Здравствуйте, садитесь (дежурный, отсутствующие).
С целью проверки качества усвоения знаний проводится дидактическая игра “Проверь себя!”. Игра состоит из двух частей. В первой части работы дети выбирают обозначение, формулу, единицы измерения, прибор для измерения одной из основных характеристик тока. Во второй части учащиеся заполняют пропуски в таблице. Класс делится на три варианта. Каждому варианту дается определенное задание. Оценивание работ проводится методом взаимопроверки.
На предыдущих занятиях мы рассмотрели три величины, с которыми мы имеем дело в любой электрической цепи, – это … (Сила тока, напряжение и сопротивление). Но в жизни и на практике недостаточно знать в отдельности физические величины, характеризующие электрические цепи, их надо рассматривать во взаимозависимости. Вот взаимозависимость мы и будем раскрывать сегодня на уроке.
Запишите тему нашего урока: “Закон Ома для участка цепи”.
О значении исследований Георга Ома точно сказал профессор физики Мюнхенского университета Ломмель Эуген Корнелиус Йозеф при открытии памятника ученому в 1895 году “Открытие Ома было ярким факелом, осветившим ту область электричества, которая до него была окутана мраком. Ом указал единственно правильный путь через непроходимый лес непонятных фактов. Замечательные успехи в развитии электротехники, за которыми мы с удивлением наблюдали в последние десятилетия, могли быть достигнуты только на основе открытия Ома. Лишь тот в состоянии господствовать над силами природы и управлять ими, кто сумеет разгадать законы природы. Ом вырвал у природы так долго скрываемую тайну и передал ее в руки современников”.
Вопрос: Какую так долго скрываемую тайну Ом вырвал у природы и передал ее в руки современников? Давайте же выясним это.
На сегодняшнем уроке нам необходимо решить следующую задачу: выяснить, как зависит сила тока на участке цепи от приложенного напряжения и величины сопротивления одновременно. Это является главной целью нашего урока.
Итак, работу на сегодняшнем уроке будем проводить по этапам.
1) Сначала установим зависимость силы тока от напряжения, запишем математически эту зависимость и проверим на опыте.
2) Установим зависимости между силой тока и сопротивлением, при постоянном напряжении; запишем результаты в таблицу, сделаем вывод о характере этой зависимости.
3) Сделаем общий вывод о том, как зависит сила тока одновременно от напряжения и сопротивления, т.е. решим основную задачу урока.
1. Установим зависимость силы тока от напряжения на опыте.
а) На демонстрационной доске собрана цепь: источник тока, реостат, амперметр, резистор, вольтметр, ключ.
б) Чертим схему цепи на доске.
в) Включаю цепь. Вольтметр показывает 2В. Какую силу тока показывает амперметр? 0,4А.
Увеличиваю напряжение до – 3В. Изменились ли показания амперметра? Да, сила тока в цепи 0,6А.
Увеличиваю напряжение до – 4В. Как изменилась сила тока? Увеличилась, сила тока в цепи 0,8А.
Запишем полученные результаты в таблицу и начертим график:
xn--i1abbnckbmcl9fb.xn--p1ai
Закон Ома для участка цепи – полученный экспериментальным (эмпирическим) путём закон, который устанавливает связь силы тока на участке цепи с напряжением на концах этого участка и его сопротивлением. Строгая формулировка закона Ома для участка цепи записывается так: сила тока в цепи прямо пропорциональна напряжению на её участке и обратно пропорциональна сопротивлению этого участка.
Формула закона Ома для участка цепи записывается в следующем виде:
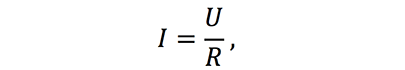
I – сила тока в проводнике [А];
U – электрическое напряжение (разность потенциалов) [В];
R – электрическое сопротивление (или просто сопротивление) проводника [Ом].
Исторически сложилось, что сопротивление R в законе Ома для участка цепи считается основной характеристикой проводника, так как зависит исключительно от параметров этого проводника. Необходимо отметить, что закон Ома в упомянутой форме справедлив для металлов и растворов (расплавов) электролитов и только для тех цепей, где нет реального источника тока или источник тока является идеальным. Идеальный источник тока – это такой источник, который не обладает собственным (внутренним) сопротивлением. Подробнее с законом Ома в применении к цепи с источником тока можно познакомится в нашей статье. Условимся считать положительным направлением слева направо (см. рисунок ниже). Тогда напряжение на участке равно разности потенциалов.
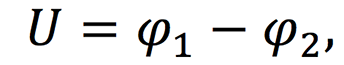
φ1 — потенциал в точке 1 (в начале участка);
φ2 — потенциал в точке 2 (а конце участка).
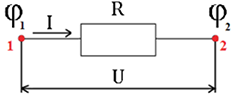
Если выполняется условие φ1 > φ2, то напряжение U > 0. Следовательно, линии напряженности в проводнике направлены от точки 1 к точке 2, а значит и ток течет в этом направлении. Именно такое направление тока будем считать положительным I > O.
Рассмотрим простейший пример определения сопротивления на участке цепи с помощью закона Ома. В результате эксперимента с электрической цепью амперметр (прибор, который показывает силу тока) показывает , а вольтметр . Необходимо определить сопротивление участка цепи .
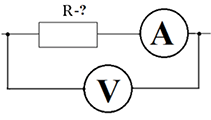
По определению закона Ома для участка цепи
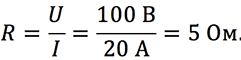
Изучая закон Ома для участка цепи в 8 классе школы, учителя часто задают ученикам следующие вопросы, чтобы закрепить пройденный материал:
Между какими величинами Закон Ома для участка цепи устанавливает зависимость?
— Правильный ответ: между силой тока [I], напряжением [U] и сопротивлением [R].
Отчего кроме напряжения зависит сила тока?
— Правильный ответ: От сопротивления
Как зависит сила тока от напряжения проводника?
— Правильный ответ: Прямо пропорционально
Как зависит сила тока от сопротивления?
— Правильный ответ: обратно пропорционально.
Данные вопросы задают для того, чтобы в 8 классе ученики смогли запомнить закон Ома для участки цепи, определение которого гласит, что сила тока прямо пропорциональна напряжению на концах проводника, если при этом сопротивление проводника не меняется.
zakon-oma.ru
Закон Ома простым языком
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:
I=U/R
Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.
Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.
Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.
Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:
f(x) = ky или f(u) = IR или f(u)=(1/R)*I
Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.
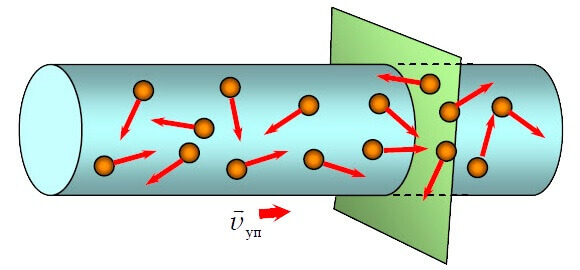
Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:
Где ρ – удельное сопротивление в Ом*мм 2 /м, L – длина в м, S – площадь поперечного сечения.
Закон Ома для параллельной и последовательной цепи
В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:
I=I1=I2
U=U1+U2
R=R1+R2
Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:
I=I1+I2
U=U1=U2
1/R=1/R1+1/R2
Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
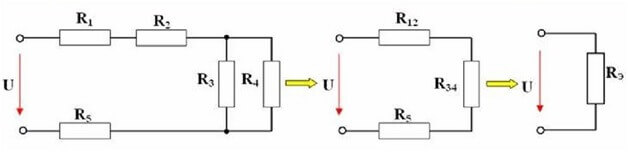
Закон Ома для полной цепи
Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:
Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.
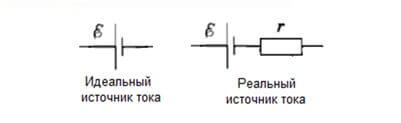
Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:
I=ε/(R+r)
Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.
На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.
Закон Ома в дифференциальной и интегральной форме
Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.
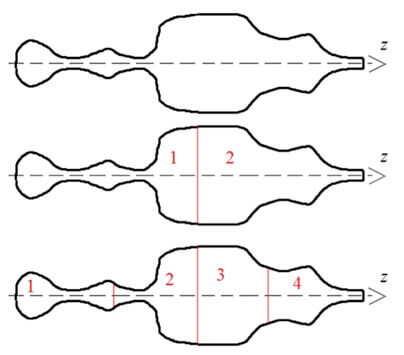
Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.
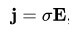
В интегральной форме:

Закон Ома для переменного тока
При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки Ra и реактивное сопротивление X (или Rr). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
- Ток в цепи с индуктивностью не может измениться мгновенно.
- Напряжение в цепи с ёмкостью не может измениться мгновенно.
Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.
U=I/Z
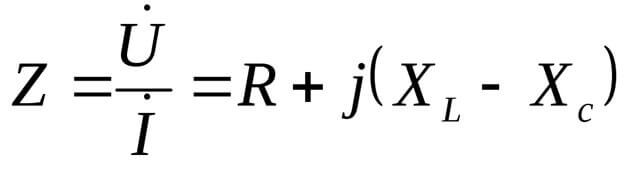
XL и XC – это реактивные составляющие нагрузки.
В связи с этим вводится величина cosФ:
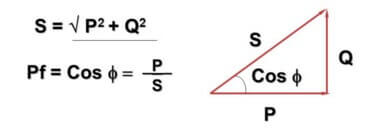
Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.
Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.
При этом сопротивление представляют в комплексной форме:

Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.
Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».
Как запомнить закон Ома
Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:
Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.
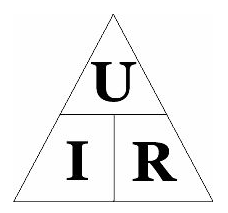
Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.

Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:

Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.

Напоследок рекомендуем просмотреть полезное видео, в котором простыми словами объясняется Закон Ома и его применение: