История появления алгебры и математики

Одним из важнейших разделов математики является алгебра. С ее помощью решаются сложные задачи в науке, технике и практической жизни человечества. Если в арифметике используются лишь 4 основных действия: сложение, вычитание, деление и умножение. В курс алгебры добавляются два новых — это возведение числа в степень и извлечение корня. Помимо натуральных, дробных чисел и нуля алгебра рассматривает отрицательные, иррациональные и другие числа. Так же, в отличие от арифметики алгебра изучает действия над всеми числами и их общие свойства. В связи с этим в алгебре различные величины обозначаются буквами, подразумевающими числа, то есть используется буквенная символика. Также, на ряду, с буквами в алгебре присутствуют числа, выраженные цифрами.

При помощи буквенной символики можно гораздо легче и проще выразить различные законы арифметики. К примеру, переместительный закон сложения, на словах звучащий так: «От перемены мест слагаемых сумма не изменяется», в алгебре можно записать гораздо проще: a + b = b + a, где a и b – любые числа. Точно так же быстро и коротко выражается на языке алгебры и переместительный закон умножения: ab = ab и другие.

Не одни лишь законы арифметики, а еще и законы множества других наук выражаются в виде формул, состоящих из букв, чисел, знаков действия и знаков равенства и неравенства. С появлением математической символики человек может выражать общие законы природы, экономя свой труд и свое время. Без математических символов в наши дни было бы очень трудно решать задачи и уравнения, особенно участвуя во всероссийском конкурсе по математике или решая важную контрольную на школьном уроке.

Зародилась алгебра в недрах арифметики, от которой длительное время она не отделялась. В арифметике древние вавилоняне, египтяне, китайцы и греки пользовались отдельными алгебраическими символами и способами решения задач. Основное развитие алгебры произошло в древней Индии, а в 9 – 15 веках – в странах ислама, включая Среднюю Азию. В начале 9 века Мухаммед ибн-Муса ал Хорезми написал книгу на арабском языке, названную «Китаб ал-джебр ва-л-мукабала». От второго слова названия этой книги, «ал-джебр», обозначающего алгебраический прием, произошло слово «алгебра», употребляемое нами сегодня. Ал-Хорезми стал первым ученым, разделившим алгебру с арифметикой и рассматривавшим ее как отдельное направление математики. Алгебру ал-Хорезми в латинском переводе изучали европейцы на протяжении 12 – 16 веков.

calvinism.ru

Законы умножения

Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:

3 + 3 + 3 + 3 = 4 + 4 + 4

Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.

Таким образом, для любых натуральных чисел a и b верно равенство:

выражающее переместительный закон умножения:

От перестановки сомножителей произведение не меняется.

Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:

3 · 2 · 4 = 3 · (2 · 4) = 3 · 8 = 24

3 · 2 · 4 = (3 · 2) · 4 = 6 · 4 = 24

Таким образом, для любых натуральных чисел a, b и c верно равенство:

выражающее сочетательный закон умножения:

Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.

Распределительный закон умножения

Для любых натуральных чисел верны равенства:

выражающие распределительный закон умножения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:

Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек. В четырёх рядах всего (3 + 5) · 4 звёздочек.

Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 · 4, а зелёных – 5 · 4. Всего звёздочек 3 · 4 + 5 · 4.

Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:

Например, 6 · (4 — 2) = 6 · 4 — 6 · 2.

Переход от умножения:

соответственно к сложению и вычитанию:

называется раскрытием скобок.

Переход от сложения и вычитания:

называется вынесением общего множителя за скобки.

naobumium.info

Презентация к уроку по алгебре (5 класс) на тему:
Распределительный закон

Урок 2 Распределительный закон

Предварительный просмотр:

Подписи к слайдам:

Математика 5 класс С.М.Никольский Подготовила : учитель математики Рафикова Наиля Ханбяловна Распределительный закон

В распределительном законе умножения относительно сложения используются круглые скобки: а ∙ (b + c) = a ∙ b + a ∙ c. Этот закон известен с глубокой древности, для его записи сначала использовали слова, затем, с введением букв, возникла потребность отделить каким-то образом выражение b + c. Круглые скобки появились впервые в XVI в. в трудах Штифеля, Тартальи и других учёных. Однако в течение всего XVII в. использовали не скобки, а горизонтальную черту. Ученики того времени применяли такую запись закона: а×b + c = a×b + а×c , где «×» — знак умножения . История возникновения

Мама попросила вас купить в магазине « Агрокомплекс» 3 пачки творога по цене 35 руб , 3 пакета молока по цене 27 руб и 3 пакета кефира по цене 33 руб. В кошельке у вас 350 рублей. Хватит ли вам денег на всю покупку? Давайте решим задачу.

1 способ: 1. 35*3=105( руб )- стоимость творога 2. 27*3=81( руб )- стоимость молока 3. 33*3=99( руб )-стоимость кефира 4. 105+81+99=285( руб )-стоимость всей покупки 2 способ: (35+27+33)*3=285 ( руб )-стоимость всей покупки 3 способ: 1.округлим цену каждого товара с избытком 2.(40+30+35)*3=315 рублей Способы решения задачи

Три пути ведут к знанию: путь размышления — это путь самый благородный, путь подражания — это путь самый легкий и путь опыта — это путь самый горький. Высказывание философа древнего Китая Конфуция

Вычислите: 37 ∙ 59 + 37 ∙ 41 + 63 ∙ 59 + 41 ∙ 63. Решить № 118(в)

Способ 1. Воспользуемся сочетательным законом сложения и сгруппируем слагаемые: 37 ∙ 59 + 37 ∙ 41 + 63 ∙ 59 + 41 ∙ 63 = (37 ∙ 59 + 37 ∙ 41) + (63 ∙ 59 + 41 ∙ 63). Воспользуемся распределительным законом сложения и вынесем за скобки общий множитель: (37 ∙ 59 + 37 ∙ 41) + (63 ∙ 59 + 41 ∙ 63) = 37 ∙ (59 + 41) + 63 ∙ (59 + 41). Найдём сумму чисел в каждой скобке (59 + 41 = 100) и воспользуемся распределительным законом сложения: 37 ∙ 100 + 63 ∙ 100 = 100 ∙ (37 + 63) = 100 ∙ 100 = 10 000. Проверка

Вычислите, используя распределительный закон: 41 ∙ 50 – 50. Решить

Представьте выражение в виде 41 ∙ 50 – 50 = 41 ∙ 50 – 1 ∙ 50. Так как множитель 50 входит в оба произведения, то его можно вынести за скобки по распределительному закону, т. е. 41 ∙ 50 – 1 ∙ 50 = 50 ∙ (41 – 1). Решение

Перепишите, заполняя пропуски: а) . · (15 + 12) = 5 · 15 + 5 · 12; б) 12 · (. + . ) = 12 · 7 + 12 · 8; в) . · (. + . ) = 14 · 15 + 14 · 29. Решить № 115

а) 5 · (15 + 12) = 5 · 15 + 5 · 12; б) 12 · (7 + 8 ) = 12 · 7 + 12 · 8; в) 14· (15 + 29) = 14 · 15 + 14 · 29. ПРОВЕРКА

Домашнее задание № 109 Обязательно выполняем № 113 второй по желанию, №111 с учетом ваших возможностей.

По теме: методические разработки, презентации и конспекты

Вашему вниманию представлена разработка урока в 5 классе по теме: «Распределительный закон умножения». Урок содержит мультимедийную презентацию. Учащиеся учатся реш.

1. систематизировать, расширить и углубить знания по данной теме 2. развивать наблюдательность, умение анализировать, вычислительные навыки.

урок «открытия нового знания».

Предлагаю материал для проведения урока по теме » Распределительный закон умножения» (урок обобщения) 6 класс.

Методическая разработка урока формирования УДД.

Пояснительная запискаТема урока «Законы арифметических действий. Распределительный закон».Тип урока – урок изучения новых знаний.Форма урока – урок-исследование. Преподав.

Тема урока «Законы арифметических действий. Распределительный закон».Тип урока – урок изучения новых знаний.Форма урока – урок-исследование. Преподавание математики в 5-м.

nsportal.ru

Законы математики

В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.

У математики есть свои законы, которые тоже надо соблюдать. Несоблюдение законов математики в лучшем случае приводит к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолеты, зависают компьютеры, крыши домов улетают от сильного ветра, качество связи снижается, кто-то голодает, а кто-то жирует.

Законы математики состоят из простых свойств. Эти свойства возможно вам уже знакомы. Но не мешает вспомнить их еще раз, а лучше всего записать или выучить наизусть.

В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.

Переместительный закон сложения

Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:

Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровняться, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нем, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.

Таким образом, между выражениями 5 +2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма будет равна

Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:

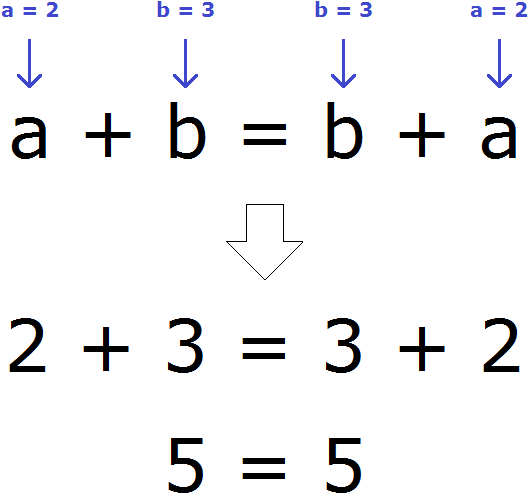
Записанное переместительное свойство сложения будет работать для любых чисел. Например, возьмем два любых числа пусть а=2 , b=3 . Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a+b=b+a и подставятся куда нужно. Число 2 подставится вместо а , число 3 место b

Сочетательный закон сложения

Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства вычислений.

Рассмотрим сумму из трех слагаемых:

Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для наглядности сумму чисел 2 и 3 можно заключить в скобки, чтобы указать, что эта сумма будет вычислена в первую очередь:

2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10

Либо сначала сложить числа 3 и 5 и сложить полученный результат с числом 2

2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10

Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку их значения равны:

(2 + 3) + 5 = 2 + (3 + 5)

Запишем сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Переместительный закон умножения

Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.

В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку их значения равны:

5 × 2 = 2 × 5

Запишем переместительное свойство умножения с помощью переменных:

Для записи законов в качестве переменных необязательно использовать именно буквы a и b . Можно использовать любые другие буквы, например c и d или x и y . Тот же переместительный закон умножения можно записать следующим образом:

Сочетательный закон умножения

Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

Рассмотрим следующее выражение:

Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:

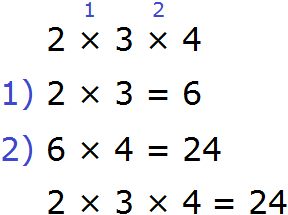
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2

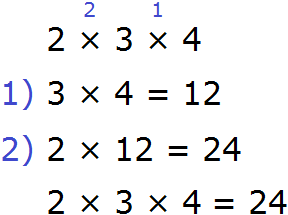
Таким образом, мы можем записать, что выражение (2 × 3) × 4 равно выражению 2 × (3 × 4) , поскольку их значения равны:

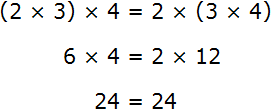
Пример 2. Найти значение выражения 1 × 2 × 3 × 4

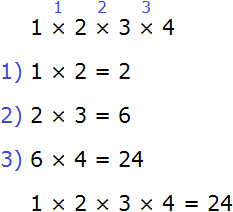
Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число или число на сумму.

Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:

В главном выражении (3+5)×2 выражение в скобках заменим на полученную восьмёрку:

8 × 2 = 16

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:

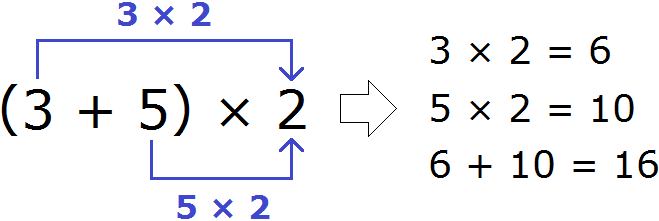
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

Теперь запишем распределительное свойство умножения с помощью переменных:

(a + b) × c = a × c + b × c

Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится. В распределительном законе умножения (a+b)×c=a×c+b×c роль множимого играет выражение (a+b) , а роль множителя переменная c . Если поменять местами множимое и множитель, то получим выражение c×(a+b) . Это умножение переменной c на сумму (a+b) . Для выполнения такого умножения, нужно применить распределительный закон умножения, то есть умножить переменную c на каждое слагаемое в скобках:

c × (a + b) = c × a + c × b

Пример 2. Найти значение выражения 5 × (3 + 2)

Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Пример 3. Найти значение выражения 6 × (5 + 2)

Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:

spacemath.xyz

Презентация по математике «Формулы сокращенного умножения»

Описание разработки

Задачи:

1. Познакомиться, с историей возникновения формул;

2. Рассмотреть, сами формулы сокращенного умножения и их применение;

3. Рассмотреть, их геометрическое обоснование.

История возникновения.

Основные законы действий над числами были известны ещё в глубокой древности и принимались как очевидные на основе многовековой человеческой практики. Но с развитием алгебры появилась и постепенно развивалась потребность в доказательстве тех или иных свойств.

В своей седьмой книге «Начал» Евклид доказывает переместительный (коммутативный) закон умножения ab=ba. Во второй книге он доказывает геометрическим методом распределительный (дистрибутивный ) закон умножения:a(b+c+d+…)=ab+ac+ad+… В дальнейшем попытка доказательства законов действий была предпринята многими учёными, в том числе Г.Ф.Лейбницем в XVIIв., Л. Эйлером, Л. Бертраном и А.М.Лежандром в XVIIIв.

Строгое же обоснование правил и законов арифметических действий было сформулировано лишь во второй половине XIXв. Тогда же были введены термины «коммутативный», или переместительный и «дистрибутивный», или распределительный, которые встречаются впервые в 1814г. У француза Сервау, а также «ассоциативный», или сочетательный, введённый в 1843г. Английским математиком В.Р.Гамильтоном.

Найденные древневавилонские клинописные тексты свидетельствуют, что формулы сокращённого умножения были известны около 4000лет назад. Их знали, кроме вавилонян, и другие народы древности, конечно, не в нашем символическом виде, а словесно или в геометрической форме, как у древних греков.

Вторая книга «Начал» Евклида содержит ряд алгебраических тождеств, сформулированных и доказанных геометрически.

Вавилоняне называли произведение ab «прямоугольником», a 2 – «квадратом», но на ряду с этим они употребляли и числа, арифметические выражения, в то время как греки старались всё переводить на геометрический язык.

В настоящее время при разложении многочленов на множители и других преобразованиях часто применяются скобки.

Содержимое разработки

В своей седьмой книге «Начал» Евклид доказывает переместительный ( коммутативный ) закон умножения ab=ba . Во второй книге он доказывает геометрическим методом распределительный ( дистрибутивный ) закон умножения: a(b+c+d+…)=ab+ac+ad+… В дальнейшем попытка доказательства законов действий была предпринята многими учёными, в том числе Г.Ф.Лейбницем в XVIIв., Л. Эйлером, Л. Бертраном и А.М.Лежандром в XVIIIв.

Строгое же обоснование правил и законов арифметических действий было сформулировано лишь во второй половине XIXв. Тогда же были введены термины « коммутативный », или переместительный и « дистрибутивный », или распределительный, которые встречаются впервые в 1814г. У француза Сервау, а также « ассоциативный », или сочетательный, введённый в 1843г. Английским математиком В.Р.Гамильтоном.

Вавилоняне называли произведение ab «прямоугольником », a 2 – «квадратом», но на ряду с этим они употребляли и числа, арифметические выражения, в то время как греки старались всё переводить на геометрический язык.

Круглые скобки появились в XVв. В трудах Штифеля, Тартальи и др. В конце того же века появляются и фигурные скобки в книгах Виета. Однако в течении почти всего XVIIв. Употреблялись не скобки, а горизонтальная черта, проводимая над выражением. Подлежащим включению в скобки. Так поступали Декарт, Гарриот и др. Ньютон пользовался даже несколькими надписанными друг над другом чертами.

Широкое применение скобок получили лишь в первой половине XVIIIв. Благодаря Лейбницу и больней степени-Эйлеру. Само название «скобки»произошло от введённого Эйлером немецкого термина Klammer-скобки.

Долгое время запись умножения не содержала знака между множителями. Такая запись стала встречаться у Диофанта при употреблении числового коэффициента, а также в индийской Бахшалийской рукописи. Косой крест х начал употребляться как знак умножения с 1631г. В XIV-XVIвв.он применялся как подсобный знак при решении самых разнообразных задач. Чтобы не смешивать косой крест с буквой x , которой обычно обозначают неизвестное, Лейбниц в конце XVIIв. Стал обозначать умножение при помощи точки.

Первая русская книга по алгебре была написана инженером Н.Е.Муравьёвым и напечатана в 1752г. В типографии Петербургской Академии наук. Однако в учебной алгебраической литературе XVIIIв. Первое место занимала «Универсальная арифметика» Леонарда Эйлера, написанная в Петербурге в 1767г. И там же вышедшая в свет на русском языке в 1768г., а на немецком- в 1770г.

Книга Эйлера сыграла большую роль в развитии математического образования не только в России, но и за рубежом. Она была переведена на шесть европейских языков и в XVIII-XIXвв. Переиздавалась по 30 раз. По образцу «Универсальной арифметики» составлялись впоследствии все учебники элементарной алгебры.

Еще в глубокой древности было замечено, что некоторые многочлены можно умножать быстрее, чем все остальные. Так, древнегреческими математиками еще до нашей эры (более 2000 лет назад) геометрическим способом были выведены некоторые формулы, которые получили название формулы сокращенного умножения .

( III век н. э.) — древнегреческий математик.

«У МАТЕМАТИКОВ СУЩЕСТВУЕТ

С. В. Ковалевская

КВАДРАТ СУММЫ ДВУХ ВЫРАЖЕНИЙ:

(а + b) 2 = а 2 + 2аb + b 2

ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА СУММЫ (а + b) 2 = а 2 + 2аb + b 2

Вместо a и b в эту формулу можно подставить любые выражения

КВАДРАТ РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ:

(а — b) 2 = а 2 — 2аb + b 2

ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА РАЗНОСТИ (а — b) 2 = а 2 — 2аb + b 2

ГЕОМЕТРИЧЕСКОЕ ОБОСНОВАНИЕ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ

Мисник Л.П. ГОУ ЦО № 975

( 1623 — 1662) — известный французский

физик, математик и философ.

Мало иметь хороший ум, главное – уметь его применять

Рене Декарт — (1596-1650) — французский философ, математик, физик и физиолог

videouroki.net