Если сила тока в колебательном контуре изменяется по закону

Последний вопрос:
24.07.2018, 10:17

Последний ответ:
19.07.2018, 14:46

Последняя рассылка:
24.07.2018, 18:15

РАЗДЕЛ • Физика

Лучшие эксперты в этом разделе

Здравствуйте! Прошу помощи в следующем вопросе:
Уважаемые эксперты! Помогите, пожалуйста.
1) Найти максимальную кинетическую энергию материальной точки массой 2г, совершающей гармонические колебания с амплитудой 4 см и частотой 5 Гц. Написать уравнение колебания, если начальная фаза 30 градусов.
2) Сила тока в колебательном контуре изменяется со временем по закону I=0.02sin400пиt(A). Индуктивность контура 0.5 Гн. Найти период собственных колебаний в контуре, электроемкость контура, максимальную энергию электрического и магнитного полей.
ОГРОМНОЕ СПАСИБО. ЗАРАНЕЕ БЛАГОДАРНА!

• Отредактировал: Сергей Фрост (Администратор)
• Дата редактирования: 23.03.2012, 09:49

Состояние: Консультация закрыта

Рассмотрим первую задачу.

Дано: m = 2 г = 2 · 10 -3 кг, A = 4 см = 4 · 10 -3 м, f = 5 Гц, φ0 = 30º = π/6.
Определить: x(t), Кмакс.

1. Находим уравнение колебания:
x(t) = A · sin (2πft + φ0) = 4 · 10 -3 · sin (10πt + π/6) (м).

2. Находим закон изменения скорости материальной точки:
v(t) = dx(t)/dt = 2пfA · cos (2πft + φ0) = 4π · 10 -2 · cos (10πt + π/6) (м/c).

При этом максимальная скорость vмакс достигается при cos (10πt + π/6) = 1: vмакс = 4π · 10 -2 м/с.

3. Находим максимальную кинетическую энергию материальной точки:
Кмакс = mvмакс 2 /2 = 2 · 10 -3 · (4π · 10 -2 ) 2 /2 ≈ 1,58 · 10 -5 (Дж).

Ответ: Кмакс ≈ 1,58 · 10 -5 (Дж); x(t) = 4 · 10 -3 · sin (10πt + π/6) (м).

0

Здравствуйте, lady.pch!
2)Сила тока в колебательном контуре изменяется со временем по закону I=0.02sin400пиt(A).Индуктивность контура 0.5Гн.Найти период собственных колебаний в контуре,электроемкость контура,максимальную энергию электрического и магнитного полей.

Уравнение колебаний в общем виде:
i=Im*sin(ω*t),
где i — мгновенное значение силы тока,
Im — максимальное значение силы тока,
ω=2*π/T.
По условию задачи имеем:
i=0.02*sin(400*π*t)
Im=0.02 (А)
ω=400*π (рад/с)
Период будет равен:
T=2*π/ω=2*π/(400*π)=0.005 (с)
Электроемкость контура равна:
C=1/(ω 2 *L)
C=1/((400*π) 2 *0.5)=1.27 (мкФ)
Максимальная разность потенциалов на обкладках конденсатора:
Um=Im*ω*L=0.02*(400*π)*0.5=12.56 (В)
Максимальная энергия магнитного поля:
Wм=Im 2 *L/2=0.02 2 *0.5/2=0.0001 (Дж)
Максимальная энергия электрического поля:
Wэ=Wm=100 (мкДж)
Будут вопросы обращайтесь в минифорум.
Удачи

• Отредактировал: Roman Chaplinsky / Химик CH (Модератор)
• Дата редактирования: 23.03.2012, 09:30

rfpro.ru

Тема 10. «Электромагнитные колебания и волны».

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид

где q» — вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ0, стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t.

Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

где- угол между нормалью к рамке и вектором магнитной индукции .

По закону электромагнитной индукции Фарадея ЭДС индукции равна

где — скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где — амплитудное значение ЭДС индукции.

2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения

Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.

Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.

называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего К 3 А, ток изменяется по закону:

i=-5000 sin100t

www.yaklass.ru

Заряд в колебательном контуре меняется по закону

Версия системы:
7.47 (16.04.2018)

Общие новости:
13.04.2018, 10:33

Последний вопрос:
18.06.2018, 13:24

Последний ответ:
18.06.2018, 11:23

Последняя рассылка:
18.06.2018, 09:15

Консультации и решение задач по физике.

[администратор рассылки: Roman Chaplinsky / Химик CH (Модератор)]

Электрический заряд на обкладках конденсатора в идеальном колебательном контуре
изменяется по закону q=0,2cos(4πt +п/3), мКл. Определить амплитуду колебаний, частоту и
период колебаний, а также максимальное значение силы тока в контуре. Построить график
колебаний заряда в конденсаторе и тока в цепи контура

Амплитуда колебаний заряда: (Кл) (мКл)

Период колебаний: (c)

Частота колебаний: (Гц)

Максимальное значение силы тока: (мА)

0

Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »

Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему.
Воспользуйтесь кнопкой входа вверху страницы, если Вы зарегистрированы или пройдите простую процедуру регистрации на Портале.

Материал для подготовки к ЕГЭ (ГИА) по физике (11 класс) на тему:
проверочная работа 11 класс тема: «Электромагнитные колебания»

6 вариантов проверочной работы по физике в 11 классе (углубленное изучение)

Предварительный просмотр:

Сила тока в колебательном контуре, содержащем катушку индуктивности 10 м Гн, меняется по закону: . Найдите:

  • Определить I m – амплитудное значение силы тока;
  • Как изменится частота, если ёмкость конденсатора уменьшить в 16 раз?
  • Определить емкость конденсатора.
  • Напишите уравнение зависимости заряда на обкладках конденсатора от времени: q = q (t),

    Заряд на обкладках конденсатора емкостью С = 1 нФ колебательного контура меняется по закону

    q=2 * 10 -6 cos(10 4 Пt) Кл.

    1. Найдите амплитуду колебаний заряда q m ;
    2. Как изменится период колебаний в идеальном колебательном контуре, если индуктивность катушки увеличиться в 6 раз?
    3. Индуктивность катушки L=?
    4. Построить график зависимости силы тока от времени i= i(t).

    Напряжение в колебательном контуре изменяется по закону: u=25sin(50Пt)В, электроёмкость конденсатора С=10 пФ

  • Как изменится циклическая частота, если в колебательном контуре заменят конденсатор на другой, с меньшей в 10 раз емкостью?
  • Найти действующую силу тока в цепи
  • Построить график зависимости силы тока в цепи от времени: i= i(t).

    Заряд в колебательном контуре с катушкой индуктивности 10 м Гн меняется по закону:

    q=2 * 10 -6 cos(500 Пt) Кл

  • Определите амплитудное значение электрического заряда q m ;
  • Определите период колебаний и циклическую частоту
  • Как изменится период колебаний, если заменят конденсатор на другой, с меньшей в 36 раз емкостью?
  • Найти напряжение на пластинах конденсатора
  • Запишите уравнение зависимости силы тока в контуре от времени i= i(t).

    Сила тока изменяется по закону: i=0,5sin(10Пt) А. Индуктивность катушки L=1 мГн.

  • Период, частоту и циклическую частоту колебаний;
  • Определить ёмкость конденсатора.
  • Как изменится частота колебаний в идеальном колебательном контуре, если емкость конденсатора уменьшится в 4 раза?
  • Напишите уравнение зависимости заряда на обкладках конденсатора от времени:q=q(t),

    Напряжение на конденсаторе 0,1 мк Ф в колебательном контуре изменяется по закону: u=20cos(10 5 Пt.)В

  • Определите амплитудное значение напряжения U m
  • Период, частоту и циклическую частоту колебаний
  • Определить индуктивность катушки L.
  • Как изменится период колебаний в идеальном колебательном контуре, если емкость конденсатора уменьшится в 9 раз?
  • Построить график зависимости заряда от времени q=q(t)

    • По теме: методические разработки, презентации и конспекты

    Проверочная работа по теме»Гипотезы происхождения жизни на Земле» составлена в форме ЕГЭ, имеет два вида заданий: с выбором одного правильного ответа, с выборм нескольких ответов.

    Данная работа включает в себя 3 задания истории России по разделу «Советское общество в 1985-1991 гг.», для двух вариантов.

    Данная работа (на два варианта) содержит 3 задания : понятийный диктант; тестовые упражнения; полный ответ на вопрос,- по «Истории России»- раздел «Российская Федерация (1991-2008 гг.)».

    «ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ,ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ».

    Проверочная работа подходит для постепенной подготовки учащихся к ЕГЭ, позволит оценить уровень подготовленности учащихся.

    Веселова Татьяна Андреевна, учитель географии ГБОУ лицея №150 Калининского района Санкт-Петербурга.Данная методическая разработка позволит учителю подготвоить учащихся 11-х классов к итоговой ат.

    Електромагнитные колебания 11кл.6 вар.1

    Электромагнитные колебания
    Вариант 1.
    Сила тока в колебательном контуре, содержащем катушку индуктивности 10 м Гн, меняется по закону: 13 EMBED Equation.3 1415. Найдите:
    Определить Im – амплитудное значение силы тока;
    Период, частоту и циклическую частоту колебаний;
    Как изменится частота, если ёмкость конденсатора уменьшить в 16 раз?
    Определить емкость конденсатора.
    Напишите уравнение зависимости заряда на обкладках конденсатора от времени: q = q (t),

    Вариант 2.
    Заряд на обкладках конденсатора емкостью С = 1 нФ колебательного контура меняется по закону
    q=2*10-6cos(104 Пt) Кл.
    Найдите амплитуду колебаний заряда qm;
    Период, частоту и циклическую частоту колебаний;
    Как изменится период колебаний в идеальном колебательном контуре, если индуктивность катушки увеличиться в 6 раз?
    Индуктивность катушки L=?
    Построить график зависимости силы тока от времени i= i(t).

    Вариант 3.
    Напряжение в колебательном контуре изменяется по закону: u=25sin(50Пt)В, электроёмкость конденсатора С=10 пФ
    Определите амплитудное значение напряжения Um
    Период, частоту и циклическую частоту колебаний
    Как изменится циклическая частота, если в колебательном контуре заменят конденсатор на другой, с меньшей в 10 раз емкостью?
    Найти действующую силу тока в цепи
    Построить график зависимости силы тока в цепи от времени: i= i(t).

    Вариант 4.
    Заряд в колебательном контуре с катушкой индуктивности 10 м Гн меняется по закону:
    q=2*10-6cos(500 Пt) Кл
    Определите амплитудное значение электрического заряда qm;
    Определите период колебаний и циклическую частоту
    Как изменится период колебаний, если заменят конденсатор на другой, с меньшей в 36 раз емкостью?
    Найти напряжение на пластинах конденсатора
    Запишите уравнение зависимости силы тока в контуре от времени i= i(t).

    Сила тока изменяется по закону: i=0,5sin(10Пt) А. Индуктивность катушки L=1 мГн.
    Определить Im – амплитудное значение силы тока;
    Период, частоту и циклическую частоту колебаний;
    Определить ёмкость конденсатора.
    Как изменится частота колебаний в идеальном колебательном контуре, если емкость конденсатора уменьшится в 4 раза?
    Напишите уравнение зависимости заряда на обкладках конденсатора от времени:q=q(t),

    Вариант 6.
    Напряжение на конденсаторе 0,1 мк Ф в колебательном контуре изменяется по закону: u=20cos(105Пt.)В
    Определите амплитудное значение напряжения Um
    Период, частоту и циклическую частоту колебаний
    Определить индуктивность катушки L.
    Как изменится период колебаний в идеальном колебательном контуре, если емкость конденсатора уменьшится в 9 раз?
    Построить график зависимости заряда от времени q=q(t)

      elektromagnitnye_kolebaniya_11kl.6_var.1
      Размер файла: 36 kB Загрузок: 0

    Решение задач по теме «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ

    Презентация к уроку

    Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

    Цели урока:

  • Образовательные: обобщение и систематизация знаний по теме, проверка знаний, умений, навыков. В целях повышения интереса к теме работу вести с помощью опорных конспектов.
  • Воспитательные: воспитание мировоззренческого понятия (причинно-следственных связей в окружающем мире), развитие у школьников коммуникативной культуры.
  • Развивающие: развитие самостоятельности мышления и интеллекта, умение формулировать выводы по изученному материалу, развитие логического мышления, развитие грамотной устной речи, содержащей физическую терминологию.

Тип урока:систематизация и обобщение знаний.

Техническая поддержка урока:

  • Демонстрации:
  • Плакаты.
  • Показ слайдов с помощью информационно – компьютерных технологий.
  • Дидактический материал:
  • Опорные конспекты с подробными записями на столах.
  • Оформление доски:
  • Плакат с кратким содержанием опорных конспектов (ОК);
  • Плакат – рисунок с изображением колебательного контура;
  • Плакат – график зависимости колебаний заряда конденсатора, напряжения между обкладками конденсатора, силы тока в катушке от времени, электрической энергии конденсатора, магнитной энергии катушки от времени.

План урока:

1. Этап повторения пройденного материала. Проверка домашнего задания.
Четыре группы задач по теме:

  • Электромагнитные колебания.
  • Колебательный контур.
  • Свободные колебания. Свободные колебания – затухающие колебания
  • Характеристика колебаний.

2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.

Учитель: Темой урока является «Решение задач по теме: «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ»

К доске вызываются 3 ученика для проверки домашнего задания.

– Задания по этой теме можно разделить на четыре группы.

Четыре группы задач по теме:

1. Задачи с использованием общих законов гармонических колебаний.
2. Задачи о свободных колебаниях конкретных колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.

– Мы остановимся на решении задач 1 и 2 групп.

Урок начнем с повторения необходимых понятий для данной группы задач.

Электромагнитные колебания – это периодические и почти периодические изменения заряда, силы тока и напряжения.

Колебательный контур – цепь, состоящая из соединительных проводов, катушки индуктивности и конденсатора.

Свободные колебания – это колебания, происходящие в системе благодаря начальному запасу энергии с частотой, определяемой параметрами самой системы: L, C.

Скорость распространения электромагнитных колебаний равна скорости света: С = 3 . 10 8 (м/с)

Основные характеристики колебаний

Амплитуда (силы тока, заряда, напряжения) – максимальное значение (силы тока, заряда, напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда, напряжения) – i, q, u

Схема колебательного контура

Учитель: Что представляют электромагнитные колебания в контуре?

Электромагнитные колебания представляют периодический переход электрической энергии конденсатора в магнитную энергию катушки и наоборот согласно закону сохранения энергии.

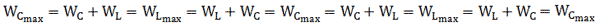
Задача №1 (д/з)

Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?

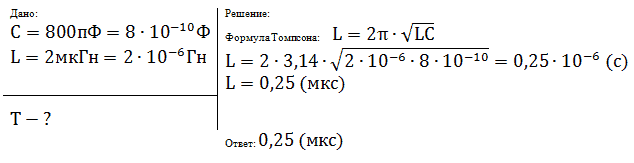
Задача № 2 (д/з)

Колебательный контур состоит из конденсатора емкостью С и катушки индуктивности индуктивностью L. Как изменится период свободных электромагнитных колебаний в этом контуре, если электроемкость конденсатора и индуктивность катушки увеличить в 3р.

Амплитуда силы тока при свободных колебаниях в колебательном контуре 100 мА. Какова амплитуда напряжения на конденсаторе колебательного контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1 Гн? Активным сопротивлением пренебречь.

Схема электромагнитных колебаний

Ученик 1 наглядно описывает процессы в колебательном контуре.

Ученик 2 комментирует электромагнитные колебания в контуре, используя графическую зависимость заряда, напряжения. Силы тока, электрической энергии конденсатора, магнитной энергии катушки индуктивности от времени.

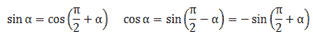
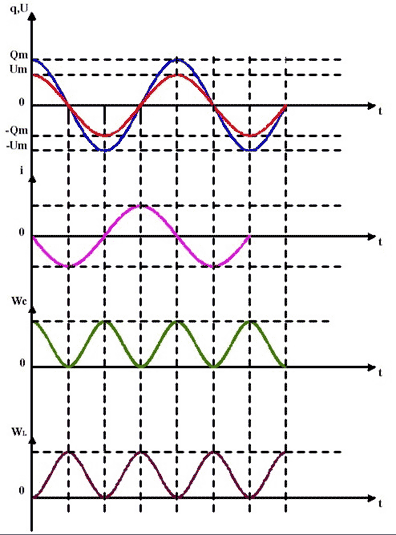
Уравнения, описывающие колебательные процессы в контуре:

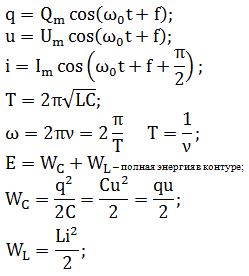
Обращаем внимание, что колебания силы тока в цепи опережают колебания напряжения между обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы тока по гармоническому закону, необходимо учитывать связь между функциями синуса и косинуса.

Задача № 1.

По графику зависимости силы тока от времени в колебательном контуре определите, какие преобразования энергии происходят в колебательном контуре в интервале времени от 1мкс до 2мкс?

Задача № 2.

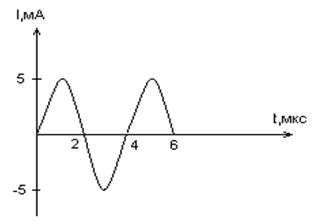
По графику зависимости силы тока от времени в колебательном контуре определите:

а) Сколько раз энергия катушки достигает максимального значения в течение первых 6 мкс после начала отсчета?
б) Сколько раз энергия конденсатора достигает максимального значения в течение первых 6 мкс после начала отсчета?
в) Определите по графику амплитудное значение силы тока, период, циклическую частоту, линейную частоту и напишите уравнение зависимости силы тока от времени.

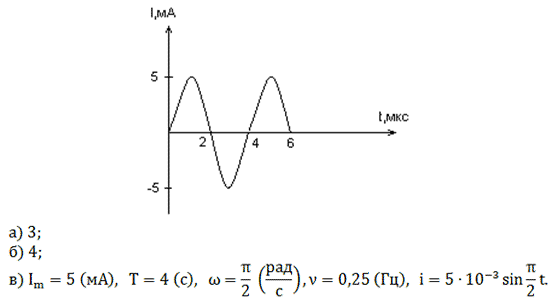
Задача № 3 (д/з)

Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите, какое преобразование энергии происходит в интервале времени от 0 до 2 мкс?

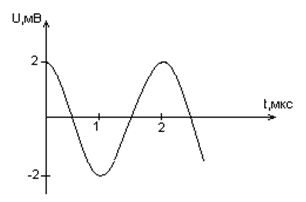
1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.

Задача № 4 (д/з)

Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите: сколько раз энергия конденсатора достигает максимального значения в период от нуля до 2мкс? Сколько раз энергия катушки достигает наибольшего значения от нуля до 2 мкс? По графику определите амплитуду колебаний напряжений, период колебаний, циклическую частоту, линейную частоту. Напишите уравнение зависимости напряжения от времени.

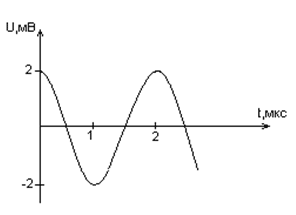
К доске вызываются 2 ученика

Задача № 5, 6

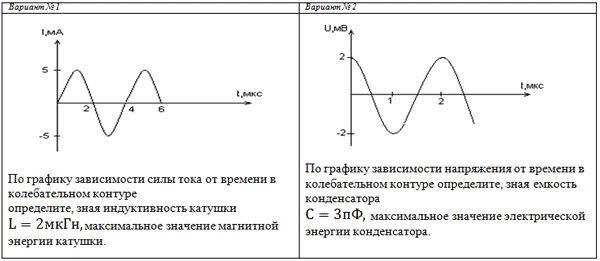
Задача № 7

Заряд на обкладках конденсатора колебательного контура изменяется по закону
q = 3·10 –7 cos800πt. Индуктивность контура 2Гн. Пренебрегая активным сопротивлением, найдите электроемкость конденсатора и максимальное значение энергии электрического поля конденсатора и магнитного поля катушки индуктивности.

Задача № 8

В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменяется заряд конденсатора в колебательном контуре с течением времени.

Электромагнитные колебания, возникающие в идеальном колебательном контуре (при отсутствии в нем активного сопротивления), описываются уравнениями, аналогичными уравнениям механических колебаний. В идеальном электромагнитном контуре заряд на обкладках конденсатора, разность потенциалов (напряжение) между его обкладками и сила тока в катушке индуктивности изменяются с течением времени по гармоническим законам.

Зависимость заряда на обкладках конденсатора от времени описывается уравнениями:

q ( t ) = q max sin ( ω t + φ 0 ) или q ( t ) = q max cos ( ω t + φ 0 ) ,

где q max — максимальное значение заряда ( амплитуда заряда ); φ — фаза колебаний, φ = ω t + φ0; φ0 — начальная фаза колебаний.

1) если колебания начинаются при полностью заряженном конденсаторе (в начальный момент времени заряд конденсатора максимален), то для описания колебаний заряда выбирают формулу

q ( t ) = q max cos ω t ;

2) если колебания начинаются при полностью разряженном конденсаторе (в начальный момент времени заряд конденсатора равен нулю), то для описания колебаний заряда выбирают формулу

q ( t ) = q max sin ω t .

Зависимость напряжения между обкладками конденсатора от времени описывается уравнениями:

U ( t ) = U max sin ( ω t + φ 0 ) или U ( t ) = U max cos ( ω t + φ 0 ) ,

где U max — максимальное значение напряжения ( амплитуда напряжения ); φ — фаза колебаний, φ = ω t + φ0; φ0 — начальная фаза колебаний.

1) если колебания начинаются при полностью заряженном конденсаторе (в начальный момент времени заряд конденсатора и разность потенциалов на его обкладках максимальны), то для описания колебаний напряжения выбирают формулу

U ( t ) = U maxcos ω t ;

2) если колебания начинаются при полностью разряженном конденсаторе (в начальный момент времени заряд конденсатора и разность потенциалов на его обкладках равны нулю), то для описания колебаний напряжения выбирают формулу

U ( t ) = U max sin ω t .

Зависимость силы тока в катушке индуктивности от времени описывается уравнениями:

I ( t ) = I max sin ( ω t + φ 0 ) или I ( t ) = I max cos ( ω t + φ 0 ) ,

где I max — максимальное значение силы тока ( амплитуда силы тока ); φ — фаза колебаний, φ = ω t + φ0; φ0 — начальная фаза колебаний.

Для упрощения этих уравнений целесообразно пользоваться правилами:

1) если электромагнитные колебания начинаются при максимальной силе тока в катушке индуктивности, то для описания колебаний силы тока выбирают формулу

I ( t ) = I max cos ω t ;

2) если электромагнитные колебания начинаются при отсутствии силы тока в катушке индуктивности, то для описания колебаний силы тока выбирают формулу

I ( t ) = I max sin ω t .

При решении задач на электромагнитные гармонические колебания следует помнить, что одно полное колебание происходит за время, равное периоду колебаний; при этом любая из величин, изменяющихся по гармоническому закону (заряд, напряжение, сила тока), проходит ряд последовательных состояний, возвращаясь в исходное состояние с начальным значением соответствующей величины:

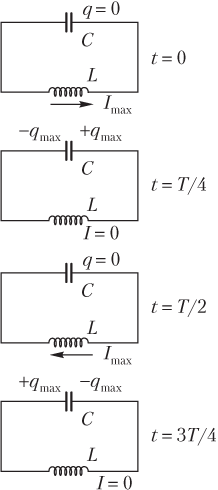
1. Если колебания начинаются при полностью заряженном конденсаторе (рис. 10.13), то через время, равное:

  • четверти периода ( t = T /4), конденсатор полностью разряжается, а в катушке индуктивности течет максимальный ток в определенном направлении;
  • половине периода ( t = T /2), ток в катушке индуктивности полностью исчезает, а на обкладках конденсатора вновь появляется максимальный заряд, однако обкладки конденсатора меняют знак (полярность);
  • трем четвертям периода ( t = 3 T /4), в катушке индуктивности сила тока вновь принимает максимальное значение, однако ток в этом случае течет в противоположном направлении;
  • периоду ( t = T ), колебательный контур возвращается в исходное состояние: конденсатор полностью заряжен, его обкладки имеют исходную полярность, ток в катушке индуктивности отсутствует.

    2. Если колебания начинаются при максимальном токе в катушке индуктивности (рис. 10.14), то через время, равное:

  • четверти периода ( t = T /4), ток в катушке полностью исчезает, а на обкладках конденсатора появляется максимальный заряд;
  • половине периода ( t = T /2), ток в катушке вновь принимает максимальное значение, однако направление тока при этом противоположно первоначальному, конденсатор полностью разряжается;
  • трем четвертям периода ( t = 3 T /4), в катушке индуктивности ток вновь отсутствует, а обкладки конденсатора заряжаются полностью, однако полярность обкладок (знак заряда) противоположная;
  • периоду ( t = T ), колебательный контур возвращается в исходное состояние: в катушке течет максимальный ток в первоначальном направлении, а конденсатор полностью разряжен.

    Мгновенные значения (значения в один и тот же произвольный момент времени) заряда на обкладках конденсатора, напряжения между ними и силы тока в катушке связаны между собой соотношениями:

      величины заряда на обкладках конденсатора и напряжения между ними —

    где q ( t ) — мгновенное значение заряда на обкладках конденсатора; C — электроемкость конденсатора; U ( t ) — мгновенное значение напряжения на его обкладках;

  • величины заряда на обкладках конденсатора и модуля силы тока в катушке индуктивности —

где I ( t ) — мгновенное значение силы тока в катушке индуктивности; ω — циклическая частота колебаний; q * ( t ) — мгновенное значение заряда на обкладках конденсатора, q * ( t ) = q maxcos(ω t + π/2).

Максимальные значения заряда на обкладках конденсатора, напряжения между ними и силы тока в катушке связаны между собой соотношениями:

величины максимального заряда на обкладках конденсатора и максимального значения напряжения —

где q max — максимальный заряд на обкладках конденсатора; C — электроемкость конденсатора; U max — максимальная разность потенциалов (напряжение) между обкладками конденсатора;

величины максимального заряда на обкладках конденсатора и максимального значения силы тока в катушке индуктивности —

где I max — максимальное значение силы тока в катушке индуктивности; ω — циклическая частота колебаний; q max — максимальный заряд на обкладках конденсатора.

Пример 10. В идеальном контуре возбуждены электромагнитные гармонические колебания, в результате которых напряжение между обкладками конденсатора изменяется по закону

U ( t ) = 0,50 cos π t / 2 ,

где U — напряжение в вольтах; t — время в секундах.

Найти величину заряда на обкладках конденсатора через 0,50 с после начала колебаний, если конденсатор имеет электроемкость 20 мкФ.

Решение . Напряжение на обкладках конденсатора изменяется по гармоническому закону и через указанное время t = 0,50 с составляет

U = 0,50 cos π / 4 = 0,25 2 В.

Величина заряда на обкладках конденсатора связана с разностью потенциалов (напряжением) между ними формулой

где q — искомый заряд в указанный момент времени; C — электроемкость конденсатора, C = 20 мкФ; U — рассчитанная разность потенциалов (напряжение) между обкладками конденсатора в тот же момент времени, U = 0,25 2 В.

Отсюда следует, что искомый заряд определяется произведением

q = 20 ⋅ 10 − 6 ⋅ 0,25 2 ≈ 7,1 ⋅ 10 − 6 Кл = 7,1 мкКл.

Через 0,50 с после начала колебаний заряд конденсатора равен 7,1 мкКл.

minjustbryansk.ru