Законы мышления в логике кратко

Основные законы логики. Закон тождества. Закон непротиворечия. Закон исключенного третьего. Закон достаточного основания.

Основные законы логики.
В логике можно выделить четыре основных закона, которые выражают коренные свойства логического мышления – его определенность, непротиворечивость, последовательность, обоснованность. К данным законам относятся: закон тождества, непротиворечия, исключенного третьего, достаточного основания. Они действуют в любом рассуждении, в какой бы логической форме оно ни протекало и какую бы логическую операцию ни выполняло. Наряду с основными логика изучает законы двойного отрицания, контрапозиции, де Моргана и т.д., которые также действуют в мышлении, обусловливая правильную связь мыслей в процессе рассуждения.

1) Закон тождества. Любая мысль в процессе рассуждения должна иметь определенное, устойчивое содержание. Это коренное свойство мышления – его определенность – выражает закон тождества: всякая мысль в процессе рассуждения должна быть тождественна самой себе (А есть А, или А = А, где А – любая мысль). Нельзя отождествлять различные мысли, нельзя тождественные мысли принимать за нетождественные. Нарушение этого требования в процессе рассуждения часто бывает связано с различным выражением одной и той же мысли в языке. С другой стороны, употребление многозначных слов может привести к ошибочному отождествлению различных мыслей. Отождествление различных мыслей часто связано с различиями в профессии, образовании и др. Отождествление различных понятий представляет собой логическую ошибку – подмену понятий, которая может быть как неосознанной, так и преднамеренной.

2) Закон непротиворечия. Логическое мышление характеризуется непротиворечивостью. Противоречия разрушают мысль, затрудняют процесс познания. Требование непротиворечивости мышления выражает формально-логический закон непротиворечия: два несовместимых друг с другом суждения не могут быть одновременно истинными; по крайней мере одно из них необходимо ложно. Данный закон формулируется следующим образом: неверно, что А и не-А (не могут быть истинными две мысли, одна из которых отрицает другую). Закон непротиворечия действует в отношении всех несовместимых суждений.

3) Закон исключенного третьего. Данный закон действует только в отношении противоречащих (контрадикторных) суждений. Он формулируется следующим образом: два противоречащих суждения не могут одновременно быть ложными, одно из них необходимо истинно: А есть либо В, либо не-В. Истинно либо утверждение некоторого факта, либо его отрицание. Противоречащие суждения – это суждения, в одном из которых что-либо утверждается (или отрицается) о каждом предмете некоторого множества, а в другом – отрицается (утверждается) о некоторой части этого множества. Эти суждения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно, то другое ложно и наоборот. Противоречащими являются также два суждения об одном предмете, в одном из которых что-либо утверждается, а в другом то же самое отрицается.

4) Закон достаточного основания. Требование доказанности, обоснованности мысли выражает данный закон: всякая мысль признается истинной, если она имеет достаточное основание. Если есть В, то есть и его основание А. Достаточным основанием мыслей может быть личный опыт человека. Истинность некоторых суждений подтверждается путем их непосредственного сопоставления с фактами действительности. Истинность законов, аксиом подтверждена практикой человечества и не нуждается поэтому в новом подтверждении. Для подтверждения какого-либо частного случая нет необходимости обосновывать его при помощи личного опыта. Достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и установленная мысль, из которой с необходимостью вытекает истинность данной.

www.tamognia.ru

Основные законы логики

4.1. Закон тождества

Первый и наиболее важный закон логики – это закон тождества, который был сформулирован Аристотелем в трактате «Метафизика» следующим образом: «…иметь не одно значение – значит не иметь ни одного значения; если же у слов нет (определённых) значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности – и с самим собой; ибо невозможно ничего мыслить, если не мыслить (каждый раз) что-нибудь одно»[4]. Можно было бы добавить к этим словам Аристотеля известное утверждение о том, что мыслить (говорить) обо всём – значит не мыслить (не говорить) ни о чём.

Закон тождества утверждает, что любая мысль (любое рассуждение) обязательно должна быть равна (тождественна) самой себе, т. е. она должна быть ясной, точной, простой, определённой. Говоря иначе, этот закон запрещает путать и подменять понятия в рассуждении (т. е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова), создавать двусмысленность, уклоняться от темы и т. п. Например, смысл простого, на первый взгляд, высказывания: «Ученики прослушали объяснение учителя», – непонятен, потому что в нём нарушен закон тождества. Ведь слово «прослушали», а значит, и всё высказывание можно понимать двояко: то ли ученики внимательно слушали учителя, то ли всё пропустили мимо ушей (причём первое значение противоположно второму). Получается, что высказывание было одно, а возможных значений у него два, т. е. – нарушается тождество: 1 ? 2. Точно так же непонятен смысл фразы: «Из-за рассеянности на турнирах шахматист неоднократно терял очки». Очевидно, что по причине нарушения закона тождества появляются неясные высказывания (суждения).

Символическая запись этого закона выглядит так: a > a (читается: «Если а, то а»), где a – это любое понятие, высказывание или целое рассуждение. Формула: a > a, является тождественно-истинной.

Когда закон тождества нарушается непроизвольно, по незнанию, тогда возникают просто логические ошибки; но когда этот закон нарушается преднамеренно, с целью запутать собеседника и доказать ему какую-нибудь ложную мысль, тогда появляются не просто ошибки, а софизмы. Таким образом, софизм – это внешне правильное доказательство ложной мысли с помощью преднамеренного нарушения логических законов. Приведём пример софизма: «Что лучше: вечное блаженство или бутерброд? Конечно же, вечное блаженство. А что может быть лучше вечного блаженства? Конечно же, ничто! Но бутерброд ведь лучше, чем ничто, следовательно, он лучше вечного блаженства». Попробуйте самостоятельно найти подвох в этом рассуждении, определить, где и как в нём нарушается закон тождества и разоблачить этот софизм. Вот ещё один софизм:

«Спросим нашего собеседника: «Согласен ли ты с тем, что если ты что-то потерял, то у тебя этого нет?» Он отвечает: «Согласен». Зададим ему второй вопрос: «А согласен ли ты с тем, что если ты что-то не терял, то у тебя это есть?» – «Согласен», – отвечает он. Теперь зададим ему последний и главный вопрос: «Ты не терял сегодня рога?» Что ему остаётся ответить? «Не терял», – говорит он. «Следовательно, – торжествующе произносим мы, – они у тебя есть, ведь ты же сам вначале признал, что если ты что-то не терял, то оно у тебя есть». Попробуйте разоблачить и этот софизм, определить, где и как в данном внешне правильном рассуждении нарушается закон тождества.

Однако на нарушениях закона тождества строятся не только неясные суждения и софизмы. С помощью нарушения этого закона можно создать какой-нибудь комический эффект. Например, Николай Васильевич Гоголь в поэме «Мёртвые души», описывая помещика Ноздрёва, говорит, что тот был «историческим человеком», потому что где бы он ни появлялся, с ним обязательно случалась какая-нибудь «история». На нарушении закона тождества построены многие комические афоризмы. Например: «Не стой где попало, а то ещё попадёт». Также с помощью нарушения этого закона создаются многие анекдоты. Например:

– Я сломал руку в двух местах.

– Больше не попадай в эти места.

Или такой анекдот:

– У вас в гостинице есть тихие номера?

– У нас все номера тихие, только вот постояльцы иногда шумят.

Как видим, во всех приведённых примерах используется один и тот же приём: в одинаковых словах смешиваются различные значения, ситуации, темы, одна из которых не равна другой, т. е. нарушается закон тождества.

Нарушение этого закона также лежит в основе многих известных нам с детства задач и головоломок. Например, мы спрашиваем собеседника: «За чем (зачем) находится вода в стеклянном стакане?» – преднамеренно создавая двусмысленность в этом вопросе (зачем – для чего и за чем – за каким предметом, где). Собеседник отвечает на один вопрос, например он говорит: «Чтобы пить, поливать цветы», а мы подразумеваем другой вопрос и, соответственно, другой ответ: «За стеклом».

Предложим нашему собеседнику такую задачу: «Как 12 разделить таким образом, чтобы получилось 7 без остатка?». Он, скорее всего, станет решать её так: 12 : x = 7; x = 12 : 7; x = ?, и скажет, что она не решается – 12 невозможно разделить так, чтобы получилось семь, да ещё и без остатка. На это мы возразим ему, что задача вполне разрешима: изобразим число 12 римскими цифрами: XII, а потом одной горизонтальной чертой разделим эту запись: XII; как видим, сверху получилось семь (римскими цифрами) и снизу тоже семь, причём без остатка. Понятно, что эта задача является софистической и основана на нарушении закона тождества, ведь её математическое решение: 12 : x = 7; x = 12 : 7; x = ? – не равно (не тождественно) её графическому решению: XII.

В основе всех фокусов также лежит нарушение закона тождества. Эффект любого фокуса заключается в том, что фокусник делает что-то одно, а зрители думают совершенно другое, т. е. то, что делает фокусник, не равно (не тождественно) тому, что думают зрители, отчего и кажется, что фокусник совершает что-то необычное и загадочное. При раскрытии фокуса нас, как правило, посещает недоумение и досада: это было так просто, как же мы вовремя этого не заметили. Например, известный иллюзионист Игорь Эмильевич Кио демонстрировал такой фокус. Он приглашал из зала человека (не подставного!) и, протягивая ему открытую записную книжку, предлагал написать там что угодно. При этом он не видел, что пишет в книжке приглашённый. Потом Кио просил вырвать из книжки страничку с написанным, вернуть ему книжку, а страничку сжечь в пепельнице.

После этого фокусник, ко всеобщему удивлению, по пеплу читал, что там было написано. «Как он это делает? – думают изумлённые зрители. – Наверное, существует какая-то хитрая методика прочтения по пеплу или ещё что-нибудь в этом роде». На самом же деле всё гораздо проще: в записной книжке фокусника через страничку после той, на которой приглашённый делает свою запись, лежит копирка, и, пока тот сжигает в пепельнице вырванную страничку, фокусник быстро и незаметно смотрит в своей книжке, что он написал.

Вот ещё один фокус – интеллектуальный. Задумайте какое-нибудь число (только не очень большое, чтобы не сложно было производить с ним различные математические операции). Теперь умножьте это число на 2 и к полученному результату прибавьте 1. Теперь умножьте то, что получилось, на 5. Далее у получившегося числа отбросьте все цифры кроме последней и к этой последней цифре прибавьте 10, потом разделите результат на 3, прибавьте к получившемуся числу 2, далее умножьте результат на 6 и прибавьте 50. У вас получилось 92. Как правило, собеседник, которому предлагается такой фокус, удивляется тому, каким образом вы узнали результат, ведь число, задуманное им, было вам неизвестно. На самом деле происходит следующее. Он задумал некое число. Для нас это x. Далее вы просите его умножить это число на 2. Результат будет чётным.

Потом вы просите прибавить 1. Результат обязательно будет нечётным. Далее вы просите его умножить этот результат на 5, а любое нечётное число, умноженное на 5, даёт новое число, которое обязательно будет оканчиваться на 5 (только не все об этом помнят). Потом вы просите собеседника отбросить у получившегося числа все цифры кроме последней и с ней производить далее различные математические действия. Таким образом, все дальнейшие операции делаются с числом 5. Эффект фокуса заключается в том, что ваш собеседник не знает о том, что вы знаете, что это 5, ведь ему по-прежнему кажется, что вам неизвестно, с каким числом производятся последующие действия. Итак, собеседник думает (или предполагает) одно, вы же делаете другое, и между первым и вторым нельзя поставить знак равенства, т. е. нарушается закон тождества.

1. О чём говорит закон тождества? Проиллюстрируйте действие этого закона с помощью какого-нибудь примера. Какая тождественно-истинная формула является выражением закона тождества?

2. Что такое софизмы? Придумайте пример какого-нибудь софизма и покажите, каким образом нарушается в нём закон тождества.

3. Определите, как нарушается закон тождества в приведённых ниже софизмах:

1) 15 – это одно число; 15 – это 7 и 8; но 7 и 8 – это два разных числа, следовательно, 15 – это два разных числа.

2) Все люди имеют глаза, значит все существа с глазами – это люди.

3) Один человек пожилого возраста доказывает, что сила его, несмотря на преклонные годы, ничуть не уменьшилась: «В юности и молодости я не мог поднять штангу весом 200 кг и сейчас не могу, стало быть, сила моя осталась прежней».

4) В одной китайской семье родилась девочка. Когда ей исполнился год, к её родителям пришёл сосед и стал сватать девочку за своего двухлетнего сына. Отец сказал: – Моей девочке всего один год, а твоему мальчику целых два, т. е. он в два раза старше её, значит, когда моей дочери будет 20 лет, твоему сыну будет уже 40. Зачем же мне выдавать свою дочь за старого жениха? Эти слова услышала жена и возразила: – Сейчас нашей дочке год, а мальчику два, однако через год ей будет тоже два и они станут ровесниками, так что вполне можно в будущем выдать нашу девочку за соседского мальчика.

4. Каким образом используются нарушения закона тождества при построении комических афоризмов, некоторых анекдотов, софистических загадок и задач? Приведите по одному примеру (за исключением тех, которые были рассмотрены в параграфе) комического афоризма, анекдота, загадки или задачи, в которых нарушается закон тождества, и покажите, в чём заключаются его нарушения.

5. Определите, как нарушается закон тождества в следующих анекдотах:

1) – Ты умеешь нырять?

– И долго под водой находишься?

– Пока кто-нибудь не вытащит.

2) Врач – пациенту:

– Каждое утро вам надо пить тёплую воду за час до завтрака.

– Как вы себя чувствуете?

– А вы выполняли мои предписания и пили каждое утро тёплую воду за час до завтрака?

– Я изо всех сил пытался это сделать, но мог её пить максимум пятнадцать минут.

3) – Ах, эти детские мечты. Сбылась ли хоть одна из них?

– У меня да. В детстве, когда мама меня причёсывала, я мечтал, чтобы у меня не было волос.

4) Учитель – ученику:

– Почему ты опоздал сегодня в школу?

– Я хотел пойти утром с отцом на рыбалку, но он меня с собой не взял.

– Надеюсь, отец тебе объяснил, почему ты должен идти в школу, а не на рыбалку?

– Да, он сказал, что червей мало и на двоих не хватит.

5) Пешеход – таксисту:

– Сколько возьмёте за проезд до центра?

– Двести рублей, садитесь.

– Спасибо, я спросил только для того, чтобы узнать, сколько я сэкономил.

6. Как нарушается закон тождества в различных фокусах? Приведите пример какого-нибудь фокуса и покажите, каким образом нарушается в нём закон тождества.

4.2. Закон противоречия

Закон противоречия говорит о том, что если одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте, в одно и то же время и в одном и том же отношении, то они не могут быть одновременно истинными. Например, два суждения: «Сократ высокий», «Сократ низкий» (одно из них нечто утверждает, а другое то же самое отрицает, ведь высокий – это не низкий, и наоборот), – не могут быть одновременно истинными, если речь идёт об одном и том же Сократе, в одно и то же время его жизни и в одном и том же отношении, т. е. если Сократ по росту сравнивается не с разными людьми одновременно, а с одним человеком. Понятно, что когда речь идёт о двух разных Сократах или об одном Сократе, но в разное время его жизни, например в 10 лет и в 20 лет, или один и тот же Сократ и в одно и то же время его жизни рассматривается в разных отношениях, например он сравнивается одновременно с высоким Платоном и низким Аристотелем, тогда два противоположных суждения вполне могут быть одновременно истинными, и закон противоречия при этом не нарушается. Символически он выражается следующей тождественно-истинной формулой: ¬ (a ? ¬ a), (читается: «Неверно, что а и не а»), где a – это какое-либо высказывание.

Говоря иначе, логический закон противоречия запрещает что-либо утверждать и то же самое отрицать одновременно. Но неужели кто-то станет нечто утверждать и то же самое тут же отрицать? Неужели кто-то будет всерьёз доказывать, например, что один и тот же человек в одно и то же время и в одном и том же отношении является и высоким, и низким или что он одновременно и толстый, и тонкий; и блондин, и брюнет и т. п.? Конечно же нет. Если принцип непротиворечивости мышления столь прост и очевиден, то стоит ли называть его логическим законом и вообще уделять ему внимание?

Дело в том, что противоречия бывают контактными, когда одно и то же утверждается и сразу же отрицается (последующая фраза отрицает предыдущую в речи, или последующее предложение отрицает предыдущее в тексте) и дистантными, когда между противоречащими друг другу суждениями находится значительный интервал в речи или в тексте. Например, в начале своего выступления лектор может выдвинуть одну идею, а в конце высказать мысль, противоречащую ей; так же и в книге в одном параграфе может утверждаться то, что отрицается в другом. Понятно, что контактные противоречия, будучи слишком заметными, почти не встречаются в мышлении и речи. Иначе обстоит дело с дистантными противоречиями: будучи неочевидными и не очень заметными, они часто проходят мимо зрительного или мысленного взора, непроизвольно пропускаются, и поэтому их часто можно встретить в интеллектуально-речевой практике. Так, Виталий Иванович Свинцов приводит пример из одного учебного пособия, в котором с интервалом в несколько страниц сначала утверждалось: «В первый период творчества Маяковский ничем не отличался от футуристов», а затем: «Уже с самого начала своего творчества Маяковский обладал качествами, которые существенно отличали его от представителей футуризма»[5].

Противоречия также бывают явными и неявными. В первом случае одна мысль непосредственно противоречит другой, а во втором случае противоречие вытекает из контекста: оно не сформулировано, но подразумевается. Например, в учебнике «Концепции современного естествознания» (этот предмет сейчас изучается во всех вузах) из главы, посвящённой теории относительности Альберта Эйнштейна, следует, что, по современным научным представлениям, пространство, время и материя не существуют друг без друга: без одного нет другого. А в главе, рассказывающей о происхождении Вселенной, говорится о том, что она появилась примерно 20 млрд лет назад в результате Большого взрыва, во время которого родилась материя, заполнившая собой всё пространство. Из этого высказывания следует, что пространство существовало до появления материи, хотя в предыдущей главе речь шла о том, что пространство не может существовать без материи[6]. Явные противоречия, так же как и контактные, встречаются редко. Неявные противоречия, как и дистантные, наоборот, в силу своей незаметности намного более распространены в мышлении и речи.

Если совместить рассмотренные выше деления противоречий на контактные и дистантные, а также на явные и неявные, то получится четыре вида противоречий:

1. Контактные и явные противоречия (можно назвать их иначе – явные и контактные, что не меняет сути).

2. Контактные и неявные противоречия.

3. Дистантные и явные противоречия.

4. Дистантные и неявные противоречия.

Примером контактного и явного противоречия может служить такое высказывание: «Водитель Н. при выезде со стоянки грубо нарушил правила, т. к. он не взял устного разрешения в письменной форме». Ещё пример контактного и явного противоречия: «Молодая девушка преклонных лет с коротким ёжиком тёмных вьющихся белокурых волос изящной походкой гимнастки, прихрамывая, вышла на сцену». Подобного рода противоречия настолько очевидны, что могут использоваться только для создания каких-нибудь комических эффектов. Остальные три группы противоречий сами по себе тоже комичны, однако, будучи неочевидными и малозаметными, они употребляются вполне серьёзно и создают значительные коммуникативные помехи. Поэтому наша задача – уметь их распознавать и устранять. Пример контактного и неявного противоречия: «Эта выполненная на бумаге рукопись создана в Древней Руси в XI в. (в XI в. на Руси ещё не было бумаги)». Пример дистантного и явного противоречия был приведён выше в виде двух высказываний о Владимире Владимировиче Маяковском из одного учебного пособия. Пример дистантного и неявного противоречия также рассмотрен выше в виде различных утверждений о взаимоотношении материи и пространства из учебника «Концепции современного естествознания».

Наконец, наверное каждому из нас знакома ситуация, когда мы говорим своему собеседнику, или он говорит нам: «Ты сам себе противоречишь». Как правило, в этом случае речь идёт о дистантных или неявных противоречиях, которые, как мы увидели, довольно часто встречаются в различных сферах мышления и жизни. Поэтому простой и даже примитивный, на первый взгляд, принцип непротиворечивости мышления имеет статус важного логического закона.

Важно отметить, что противоречия также бывают мнимыми.

Некая мыслительная или речевая конструкция может быть построена так, что, на первый взгляд, выглядит противоречивой, хотя на самом деле никакого противоречия в себе не содержит. Например, известное высказывание Антона Павловича Чехова: «В детстве у меня не было детства», – кажется противоречивым, т. к. оно вроде бы подразумевает одновременную истинность двух суждений, одно из которых отрицает другое: «У меня было детство», «У меня не было детства». Таким образом, можно предположить, что противоречие в данном высказывании не просто присутствует, но и является наиболее грубым – контактным и явным. На самом же деле никакого противоречия в чеховской фразе нет. Вспомним, закон противоречия нарушается только тогда, когда речь идёт об одном и том же предмете, в одно и то же время и в одном и том же отношении. В рассматриваемом высказывании речь идёт о двух разных предметах: термин «детство» употребляется в различных значениях: детство как определённый возраст; детство как состояние души, пора счастья и безмятежности. Хотя и без этих комментариев, скорее всего, вполне понятно, что хотел сказать Антон Павлович Чехов. Обратим внимание на то, что кажущееся противоречие использовано им, по всей видимости, преднамеренно, для достижения большего художественного эффекта. И действительно, благодаря ненастоящему противоречию яркое и запоминающееся чеховское суждение стало удачным афоризмом. Таким образом, мнимое противоречие можно использовать как художественный приём. Достаточно вспомнить названия известных литературных произведений: «Живой труп» (Л. Н. Толстой), «Мещанин во дворянстве» (Ж. Мольер), «Барышня-крестьянка» (А. С. Пушкин), «Горячий снег» (Ю. В. Бондарев) и др. Иногда на мнимом противоречии строится заголовок газетной или журнальной статьи: «Знакомые незнакомцы», «Древняя новизна», «Необходимая случайность» и т. п.

Итак, закон противоречия запрещает одновременную истинность двух суждений, одно из которых нечто утверждает, а другое то же самое отрицает об одном и том же предмете, в одно и то же время и в одном и том же отношении. Однако этот закон не запрещает одновременную ложность двух таких суждений. Вспомним, суждения:

«Он высокий», «Он низкий», – не могут быть одновременно истинными, если речь идёт об одном и том же человеке, в одно и то же время его жизни и в одном и том же отношении (относительно какого-то одного образца для сравнения). Однако эти суждения вполне могут быть одновременно ложными при соблюдении всех вышеперечисленных условий. Если истинным будет суждение: «Он среднего роста», – тогда суждения: «Он высокий», «Он низкий», – придётся признать одновременно ложными. Точно так же одновременно ложными (но не одновременно истинными!) могут быть суждения:

«Эта вода горячая», «Эта вода холодная»; «Данная речка глубокая», «Данная речка мелкая»; «Эта комната светлая», «Эта комната тёмная». Одновременную ложность двух суждений мы часто используем в повседневной жизни, когда, характеризуя кого-то или что-то, строим стереотипные обороты типа: «Они не молодые, но и не старые», «Это не полезно, но и не вредно», «Он не богат, однако и не беден», «Данная вещь стоит не дорого, но и не дёшево», «Этот поступок не является плохим, но в то же время его нельзя назвать хорошим».

1. О чём говорит закон противоречия? Объясните, почему этот закон не действует, если речь идёт о разных объектах, в разное время и в различном отношении. Проиллюстрируйте действие закона противоречия с помощью какого-нибудь самостоятельно подобранного примера. Какая тождественно-истинная формула является выражением закона противоречия?

2. Если логический принцип непротиворечивости мышления настолько прост и очевиден, то почему он возводится в ранг одного из основных законов логики?

3. Что такое контактные и дистантные противоречия? Придумайте по одному примеру контактных и дистантных противоречий.

4. Что такое явные и неявные противоречия? Придумайте по одному примеру явных и неявных противоречий. Почему дистантные и неявные противоречия встречаются в интеллектуально-речевой практике намного чаще, чем контактные и явные?

5. На какие четыре группы можно разделить все противоречия?

Найдите в художественной, публицистической, научной и учебной литературе по одному примеру для следующих видов противоречий: контактных и неявных, дистантных и явных, дистантных и неявных.

6. Что такое мнимые противоречия? Приведите два или три примера мнимых противоречий (за исключением тех, которые были рассмотрены в параграфе). Подумайте, почему мнимое противоречие часто используется в качестве художественного приёма?

7. В известной песне «Подмосковные вечера» есть такие слова:

«…речка движется и не движется… песня слышится и не слышится…». Реальное или мнимое противоречие представляет собой эта фраза? Обоснуйте свой ответ.

8. Все помнят знаменитые слова из сказки Александра Сергеевича Пушкина: «Кто на свете всех милее, всех румяней и белее?» Возможно, вы и раньше задумывались над тем, как можно быть румяней и белее одновременно. Реальное или мнимое противоречие присутствует в данном высказывании? Обоснуйте свой ответ.

9. Могут ли два суждения, одно из которых что-либо утверждает, а другое то же самое отрицает об одном и том же предмете, в одно и то же время и в одном и том же отношении, быть одновременно ложными? Если могут, то приведите несколько примеров таких суждений.

4.3. Закон исключённого третьего

Суждения бывают противоположными и противоречащими. Например, суждения: «Сократ высокий», «Сократ низкий», – являются противоположными, а суждения: «Сократ высокий», «Сократ невысокий», – противоречащими. В чём разница между противоположными и противоречащими суждениями? Нетрудно заметить, что противоположные суждения всегда предполагают некий третий, средний, промежуточный вариант. Для суждений: «Сократ высокий», «Сократ низкий», – третьим вариантом будет суждение: «Сократ среднего роста». Противоречащие суждения, в отличие от противоположных, не допускают или автоматически исключают такой промежуточный вариант. Как бы мы ни пытались, мы не сможем найти никакого третьего варианта для суждений: «Сократ высокий», «Сократ невысокий» (ведь и низкий, и среднего роста — это всё невысокий).

Именно в силу наличия третьего варианта противоположные суждения могут быть одновременно ложными. Если суждение: «Сократ среднего роста», – является истинным, то противоположные суждения: «Сократ высокий», «Сократ низкий», – одновременно ложны.

Точно так же именно в силу отсутствия третьего варианта противоречащие суждения не могут быть одновременно ложными. Таково различие между противоположными и противоречащими суждениями. Сходство между ними заключается в том, что и противоположные суждения, и противоречащие не могут быть одновременно истинными, как того требует закон противоречия. Таким образом, этот закон распространяется и на противоположные суждения, и на противоречащие. Однако, как мы помним, закон противоречия запрещает одновременную истинность двух суждений, но не запрещает их одновременную ложность; а противоречащие суждения не могут быть одновременно ложными, т. е. закон противоречия является для них недостаточным и нуждается в каком-то дополнении. Поэтому для противоречащих суждений существует закон исключённого третьего, который говорит о том, что два противоречащих суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными (истинность одного из них обязательно означает ложность другого, и наоборот). Символическая запись закона исключённого третьего представляет собой следующую тождественно-истинную формулу: a 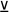¬ a (читается – «а или не а»), где a – это какое-либо высказывание.

1. В чём различие между противоположными и противоречащими суждениями? Почему противоположные суждения могут быть одновременно ложными, а противоречащие – не могут?

2. В чём сходство между противоположными и противоречащими суждениями? Почему закон противоречия является недостаточным для противоречащих суждений и нуждается в дополнении?

3. О чём говорит закон исключённого третьего? Какая тождественно-истинная формула является его выражением? В каком отношении находится закон исключённого третьего к закону противоречия?

4.4. Закон достаточного основания

Закон достаточного основания утверждает, что любая мысль (тезис) для того, чтобы иметь силу, обязательно должна быть доказана (обоснована) какими-либо аргументами (основаниями), причём эти аргументы должны быть достаточными для доказательства исходной мысли, т. е. она должна вытекать из них с необходимостью (тезис должен с необходимостью следовать из оснований).

Приведём несколько примеров. В рассуждении: «Это вещество является электропроводным (тезис), потому что оно – металл (основание)», – закон достаточного основания не нарушен, так как в данном случае из основания следует тезис (из того, что вещество металл, вытекает, что оно электропроводно). А в рассуждении:

«Сегодня взлётная полоса покрыта льдом (тезис), ведь самолёты сегодня не могут взлететь (основание)», – рассматриваемый закон нарушен, тезис не вытекает из основания (из того, что самолёты не могут взлететь, не вытекает, что взлётная полоса покрыта льдом, ведь самолёты могут не взлететь и по другой причине). Так же нарушается закон достаточного основания в ситуации, когда студент говорит преподавателю на экзамене: «Не ставьте мне двойку, спросите ещё (тезис), я же прочитал весь учебник, может быть, и отвечу что-нибудь (основание)». В этом случае тезис не вытекает из основания (студент мог прочитать весь учебник, но из этого не следует, что он сможет что-то ответить, так как он мог забыть всё прочитанное или ничего в нём не понять и т. п.).

В рассуждении: «Преступление совершил Н. (тезис), ведь он сам признался в этом и подписал все показания (основание)», – закон достаточного основания, конечно же, нарушен, потому что из того, что человек признался в совершении преступления, не вытекает, что он действительно его совершил. Признаться, как известно, можно в чём угодно под давлением различных обстоятельств (в чём только не признавались люди в застенках средневековой инквизиции и кабинетах репрессивных органов власти, в чём только не признаются на страницах бульварной прессы, в телевизионных ток-шоу и т. п.!).

Таким образом, на законе достаточного основания базируется важный юридический принцип презумпции невиновности, который предписывает считать человека невиновным, даже если он даёт показания против себя, до тех пор, пока его вина не будет достоверно доказана какими-либо фактами.

Закон достаточного основания, требуя от любого рассуждения доказательной силы, предостерегает нас от поспешных выводов, голословных утверждений, дешёвых сенсаций, слухов, сплетен и небылиц. Запрещая принимать что-либо только на веру, этот закон выступает надёжной преградой для любого интеллектуального мошенничества. Не случайно он является одним из главных принципов науки (в отличие от псевдонауки или лженауки).

1. Что представляет собой закон достаточного основания? Приведите три примера (за исключением тех, которые рассмотрены в параграфе) нарушений этого закона.

2. Что представляет собой юридический принцип презумпции невиновности? Каким образом он связан с законом достаточного основания?

3. Какую роль играет закон достаточного основания в обыденном мышлении и повседневной жизни? Отвечая на этот вопрос, надо принять во внимание, что человеку, как это ни печально, свойственно лгать. Довольно часто мы произносим эмоциональную фразу:

«Какой смысл ему (ей, им) меня обманывать?». Увы, смысл иногда есть. Причём нередко человек лжёт не из-за чего-то или для чего-то, а неосознанно, безотчётно. Одной из разновидностей такой лжи является ситуация, когда собеседник, рассказывая какую-нибудь небылицу про себя или просто приукрашивая действительность, обманывает не только и не столько нас, сколько самого себя, поскольку в это время пребывает в вымышленном и приятном ему мире собственных фантазий.

4. Выделите исходную мысль (тезис) и аргументы (основание) в приведённых ниже рассуждениях и определите, нарушен ли в них закон достаточного основания:

1) Эти две прямые параллельны, поскольку у них нет общих точек.

2) Эти две прямые параллельны, т. к. они лежат в одной плоскости и не имеют общих точек.

3) Данное вещество является металлом, потому что оно электропроводно.

4) Мой товарищ зарабатывает 10 000 долл. в месяц, в чём нельзя усомниться, ведь он сам это утверждает.

5) В одном американском штате потерпела крушение летающая тарелка, ведь об этом писали в газетах, это передавали по радио и даже показывали по телевидению.

6) Сегодня корабли не могут заходить в бухту, потому что она заминирована.

7) Этот человек не болен, ведь у него не повышена температура.

8) Данное слово надо писать с большой буквы, т.к. оно стоит в начале предложения.

5. Установите, какой из основных законов логики – тождества, противоречия, исключённого третьего, достаточного основания – нарушен в следующих примерах:

1) – Почему вы называете этот хор смешанным? Ведь здесь одни женщины.

– Да, но одни умеют петь, а другие – нет.

2) Когда Майкл Фарадей обратился к Гемфри Дэви с просьбой принять его на работу в лабораторию, тот спросил совета у одного из руководителей Королевского института. «Поручи ему, – был ответ, – мыть лабораторную посуду. Если он к чему-нибудь способен, то обязательно согласится; если же не согласится, значит не способен ни к чему».

«Бабин вынул трубку изо рта. Смеясь одними глазами, спросил:

– Обожди, Маклецов, ты «Лес» читал?

– Я за войну ни одной книги не прочёл, – сказал Маклецов с достоинством.

– Ну это тебе полагалось ещё до войны прочесть.

– А раз полагалось, значит, прочёл.

– Всё-таки: читал или не читал?

– Да что вы навалились, товарищ комбат, всякую инициативу сковываете! Лес. Я в сорок первом в окружении, в таких лесах воевал, какие тому Островскому сроду не снились…»

((Г. Я. Бакланов. Военные повести))

4) «Маловысокохудожественное произведение». (М. М. Зощенко)

5) Желая узнать, имеет ли воздух вес, Аристотель надул им бычий пузырь и взвесил его. Потом выпустил из него воздух и снова взвесил. Вес в обоих случаях оказался одинаковым. Из этого философ сделал вывод, что воздух невесом.

«Религия повергает человечество на колени перед существом, не обладающим протяжённостью и, вместе с тем, бесконечным и всё наполняющим своей безмерностью; перед существом всемогущим и никогда не выполняющим своих желаний; перед существом бесконечно добрым и возбуждающим одно недовольство; перед существом, стремящимся к гармонии и всюду сеющим раздоры и беспорядок».

«Алиса встречает Белого Короля. Он говорит:

– Взгляни-ка на дорогу! Кого ты там видишь?

– Никого, – сказала Алиса.

– Мне бы такое зрение! – заметил Король с завистью. – Увидеть Никого! Да ещё на таком расстоянии!»

((Л. Кэролл. Алиса в Зазеркалье))

8) Девка с полными вёдрами – к добру; пустые вёдра – к худу.

9) Учащийся спрашивает учителя: «Можно ли ругать или наказывать человека за то, что он не сделал?»

– «Нельзя», – отвечает учитель.

– «В таком случае не ругайте и не наказывайте меня, – говорит учащийся, – я не сделал сегодня домашнее задание».

10) – Дай мне одну из твоих собак.

– Чёрная мне милее белой!

– Тогда дай белую.

– А белая мне милее обеих!

«– А что, отец, – спросил молодой человек, затянувшись, – невесты у вас в городе есть?

– Кому и кобыла невеста, – ответил старик, охотно ввязываясь в разговор».

((И. Ильф, Е. Петров. Двенадцать стульев))

12) Вот я к Вам приехал в среду, Но уж больше не приеду; Ведь попал я на беду В очень скучную среду. И могу сказать Вам смело: Всех гостей «среда заела!» (Н. Врангель)

«– Прекрасно! – промолвил Рудин. – Стало быть, по-вашему, убеждений нет?

– Нет и не существует.

– Это ваше убеждение?

– Как же вы говорите, что их нет? Вот вам уже одно, на первый случай».

((И. С. Тургенев. Рудин))

Примечания:

Сборник упражнений по логике. – Минск: Университетское, 1990. – С. 95.

См.: Свинцов В. И. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998. – С.144.

См.: Концепции современного естествознания / Под ред. В. Н. Лавриенко, В. П. Ратникова. – М.: ЮНИТИ, 1987. – С. 106 – 127.

www.k2x2.info