2.3. Законы Ома в интегральной форме

Закон Ома в интегральной форме подразумевает, что рассматривается полный ток, протекающий в цепи и величина тока со временем не меняется. Очевидно, что количество заряда, протекающее по проводнику, обратно пропорционально сопротивлению проводника. Количество заряда протекающее в проводнике, прямо пропорционально напряженности или разности потенциалов, создающих внешнее электрическое поле.

1) — закон Ома для участка цепи, не содержащего э.д.с.

Суммарное сопротивление проводников и элементов цепи без э.д.с. обозначается на схеме.

2) Если участок цепи включает в себя э.д.с, то собственное сопротивление источника тока выделяется и обозначается r.

Тогда закон Ома для участка цепи, содержащей э.д.с., будет иметь вид:

.

3) Если замкнутый участок цепи, содержит э.д.с., тогда φ1 = φ2, и получаем:

— закон Ома для замкнутого участка цепи, содержащего э.д.с.

В целом участок цепи, содержащей множество э.д.с. и разных деталей представлен законом Ома в виде:

.

Если при напряжении на концах участка цепи в 1В по цепи протекает ток в 1А, то говорят, что сопротивление цепи равно одному Ому.

Из закона Ома следует:

.

2.3.1. Закон Ома в дифференциальной форме

Сечение проводника или элементов цепи, как правило, неоднородно, и сопротивляемость в разных участках цепи протеканию тока также различная. Тогда разбивают участки цепи на элементы (дифференцируют) и определяют закон Ома в каждом отдельном участке.

— закон Ома, тогда для каждого участка цепи сечением ∆ S и длиной ∆ l можно записать закон Ома как:
.

Учитывая, что для участка цепи

и , получим .

Это закон Ома в дифференциальной форме. Зная, что удельная электропроводность σ и удельное сопротивление ρ связаны, как:

,
где

σ — удельная электропроводность,

ρ — удельная сопротивление,

— закон Ома в дифференциальной форме.

siblec.ru

Методические указания к лабораторной работе №23


Загрузить всю книгу

3.1.3. Законы постоянного тока

1) Закон Ома – это экспериментальный закон, согласно которому сила тока, текущего по проводнику, пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

.

Соотношение (13) иначе называют законом Ома в интегральной форме записи. Это соотношение можно распространить на отдельные участки и всю замкнутую электрическую цепь, учитывая формулы (10), (11), (12) и внутреннее сопротивление источника тока r. При этом получим частные случаи закона Ома:

а) неоднородный участок цепи (рис. 2):

.

Формулу (14) называют обобщённым законом Ома в интегральной форме записи;

б) однородный участок цепи (рис. 3):

;

в) цепь замкнута (рис. 4) :

.

Электрическое сопротивление ( R ) характеризует противодействие проводника электрическому току и зависит от формы, размеров и материала проводника. Измеряется сопротивление R в омах (Ом).

Для однородного цилиндрического проводника длиной l и поперечным сечением S :

,

где ρ – удельное сопротивление проводника. Оно зависит от материала проводника и условий протекания тока, в частности, от температуры. Для большинства металлов при температурах, близких к комнатной, удельное сопротивление изменяется пропорционально температуре T:

,

где ρ0 – удельное сопротивление проводника при 0ºС (T = 273 К). Удельное сопротивление ρ измеряется в ом-метрах (Ом·м).

Закон Ома в дифференциальной форме записи можно получить, если рассмотреть бесконечно малый участок проводника длиной dl и поперечным сечением dS (рис. 5).

Рис. 5. К выводу закона Ома в дифференциальной форме записи (обозначения в тексте)

Сопротивление этого участка:

.

Напряжение на концах проводника dU , совпадающее с разностью потенциалов, связано с напряжённостью E электрического поля соотношением:

.

Через сечение dS течёт ток, плотность которого согласно соотношению (4):

.

Подставляя значения R и U по формулам (19) и (20) в закон Ома (13), получаем:

,

,

или, с учётом соотношения (21),

,

где – удельная проводимость проводника.

Учитывая, что направления и совпадают, соотношение (22) можно записать в векторном виде:

.

Это и есть дифференциальная форма записи закона Ома для однородного участка проводника. На неоднородном участке, кроме электростатического поля с напряжённостью , действует поле сторонних сил, напряжённость которого – стор; в этом случае:

.

Соотношение (24) является законом Ома в дифференциальной форме записи для неоднородного участка проводника.

2) Закон Джоуля-Ленца характеризует тепловое действие тока. При протекании электрического тока проводник нагревается, при этом выделяется количество теплоты Q т, определяемое соотношениями:

.

3) Правила Кирхгофа значительно упрощают расчёт разветвлённых электрических цепей. Пример такой цепи показан на рис. 6.

Рис. 6. Разветвлённая электрическая цепь

Правил Кирхгофа два:

а) I правило Кирхгофа относится к узлам электрической цепи.

Узлом цепи называется точка, в которой сходится не менее трёх проводни­ков. В схеме на рис. 6 два узла – В и К.

Согласно I правилу Кирхгофа алгебраическая сумма сил токов, сходящихся в узле, равна нулю:

.

Прежде чем применять I правило Кирхгофа, необходимо проставить направления токов и значения сил токов в различных ветвях электрической цепи (ветвь – участок цепи, соединяющий узлы). Если трудно указать истинное направление тока, его проставляют произвольно. Если направление тока на каком-то участке проставлено неверно, то значение силы тока на этом участке в результате решения задачи получается отрицательным. Условились считать, что токи, входящие в узел (текущие к узлу), считаются положительными, и при записи соотношения (26) берутся со знаком «+», а токи, выходящие из узла, – со знаком «–». Например, для узла К соотношение (26) примет вид:

.

I правило Кирхгофа является следствием закона сохранения заряда для цепей постоянного электрического тока. В случае постоянного тока заряды в узлах накапливаться не должны, и количество зарядов, входящих в узел, должно равняться количеству зарядов, выходящих из узла. Если в цепи N узлов, то линейно независимых уравнений можно записать только для ( N –1) узла, уравнение для N -ого узла будет следствием предыдущих. Например, уравнение для узла В (рис. 6) будет повторением уравнения (27);

б) II правило Кирхгофа является следствием закона Ома и относится к любому выделенному в разветвлённой цепи замкнутому контуру.

Согласно этому правилу сумма падений напряжений равна сумме действующих в контуре ЭДС:

.

Так как по закону Ома , то соотношение (28) можно записать так:

.

Прежде чем применять II правило Кирхгофа к какому-либо контуру, в нём совершенно произвольно выбирается направление обхода (например, по часовой стрелке). При этом напряжение считается положительным и берётся в уравнении (29) со знаком «+», если ток на данном сопротивлении совпадает с направлением обхода контура. ЭДС источника берётся в уравнении (29) со знаком «+», если источник создаёт ток (при условии, что других источников тока нет) в направлении обхода контура. Например, II правило Кирхгофа для контура АМКВ (рис. 6) будет иметь следующий вид:

.

Видим, что удобнее было бы взять направление обхода контура в противоположную сторону.

Для контура ВКДС соотношение (29) запишется так:

.

Уравнение (29) может быть составлено для всех замкнутых контуров, которые можно выделить в разветвлённой цепи (на рис. 6 их три: АМКВ, ВКДС, АМДС). Однако независимыми будут уравнения только для тех контуров, которые нельзя получить наложением других, уже использованных (например, контур АМДС является суммой контуров АМКВ и ВКДС). Оказывается, что количество независимых уравнений, составленных в соответствии с I и II правилами Кирхгофа, равно числу различных токов, текущих в разветвлённой электрической цепи. Решая совместно уравнения (27), (30), (31), можно найти любые три неизвестные характеристики электрической цепи, показанной на рис. 6.

edu.tltsu.ru

Закон Ома в дифференциальной форме;

Сопротивление 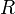зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

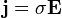
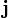§ — вектор плотности тока,

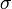§ — удельная проводимость,

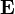§ — вектор напряжённости электрического поля.

В дифференциальной форме
Закон Ома для участка электрической цепи имеет вид:
U = RI

где:
U — напряжение или разность потенциалов,
I — сила тока,
R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
I=E/(R+r),

где:
e — ЭДС цепи,
I — сила тока в цепи,
R — сопротивление всех элементов цепи,
r — внутреннее сопротивление источника питания.

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
j=σ*E

где
j- вектор плотности тока,
σ — удельная проводимость,
E — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

33 Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 годуДжеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцом [1] .

В словесной формулировке звучит следующим образом [2]

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведениюплотности электрического тока на величину электрического поля

Математически может быть выражен в следующей форме:

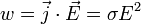
где w — мощность выделения тепла в единице объёма, 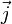— плотность электрического тока, 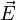— напряжённость электрического поля, σ —проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах [3] :

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадратасилы тока на этом участке и сопротивлению участка

В математической форме этот закон имеет вид

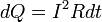
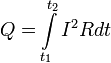
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:

studopedia.su

Закон Ома в интегральной форме

Для того, чтобы перейти к интегральной форме записи закона Ома для участка проводника, на котором действуют две силы, введем понятие линии тока.

Линия тока – кривая, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. В этом случае вектор плотности находится из соотношения:

где τ ⃗ – единичный вектор касательной к линии тока.

Предположим, что удельное сопротивление (r) и напряженность поля движущих сил (E ⃗) на поперечном сечении проводника однородны, т.к. E ⃗ однородна, то j ⃗ так же однородная величина. Возьмем произвольное значение поперечного сечения цепи – S. Тогда:

, а значит

Последнее равенство до множим на dl (элементарное перемещение вдоль вектора плотности тока):

где

  • dφ – элементарный сброс потенциала электростатического поля,
  • dε – элементарная работа сторонних сил по перемещению единичного положительного заряда (ЭДС).

Отсюда:

Учитывая, что ρ/S dl=dR (элементарное сопротивление), запишем закон Ома в интегральной форме:

Закон Ома в интегральной форме для неоднородного участка цепи

Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:

интегральный закон Ома для участка цепи

  • – сопротивление участка,
  • – работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,
  • – работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),
  • – абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).

    • Запишем значение напряжения при постоянном токе:

    Отсюда запишем закон Ома:

    Таким образом закон Ома в интегральной форме – это закон изменения механической энергии единичного положительного заряда на этом участке. В арифметическом виде этот закон можно записать так:

    Решение задач

    Какой будет плотность тока в металлическом проводнике с удельным сопротивлением ρ постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?

    zakon-oma.ru

    Закон ома для участка цепи в интегральной и дифференциальной формах

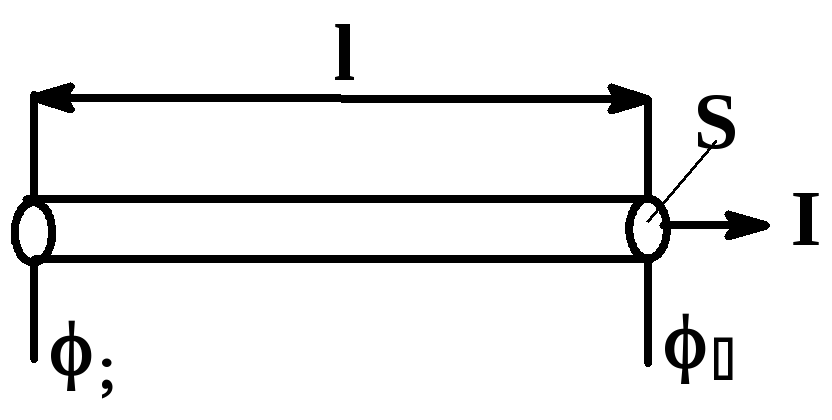
    Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а 1 и 2 – потенциалы на концах проводника. В случае однородного проводника величину 1 — 2 = U можно назвать падением напряжения на участке проводника.

    Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:

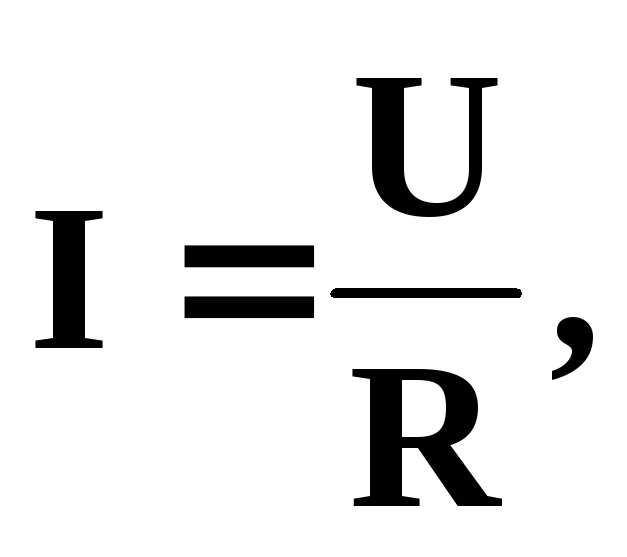
    — закон Ома в интегральной форме

    где R – электрическое сопротивление проводника.

    Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.

    Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника

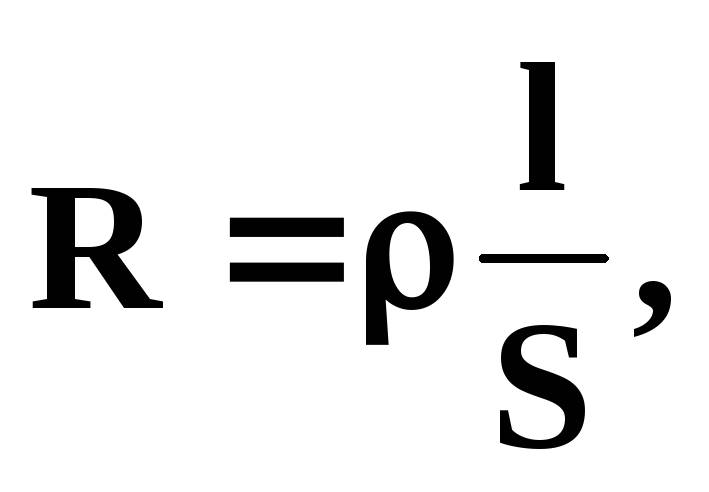
    где — удельное сопротивление проводника.

    Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м 2 . Размерность удельного сопротивления в СИ: [] = Омм.

    Величина, обратная сопротивлению, называется проводимостью.

    Величина, обратная удельному сопротивлению, называется удельной проводимостью:

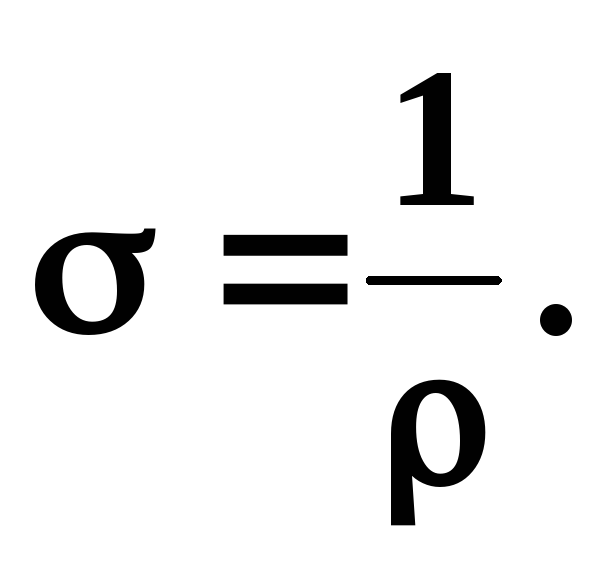
    Учитывая выше написанные уравнения, а также , получим:

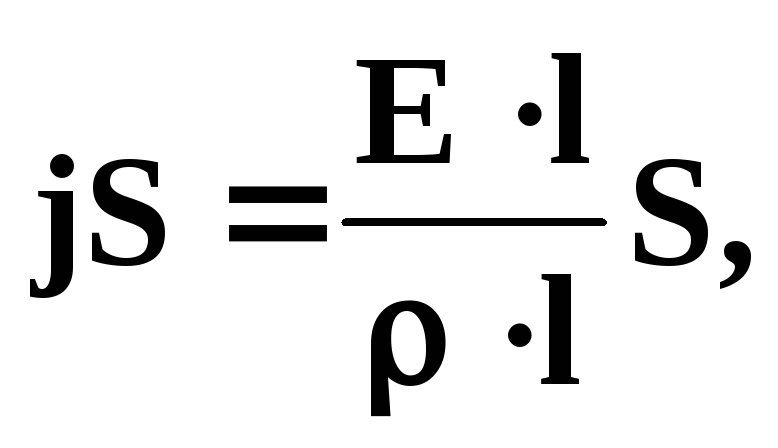
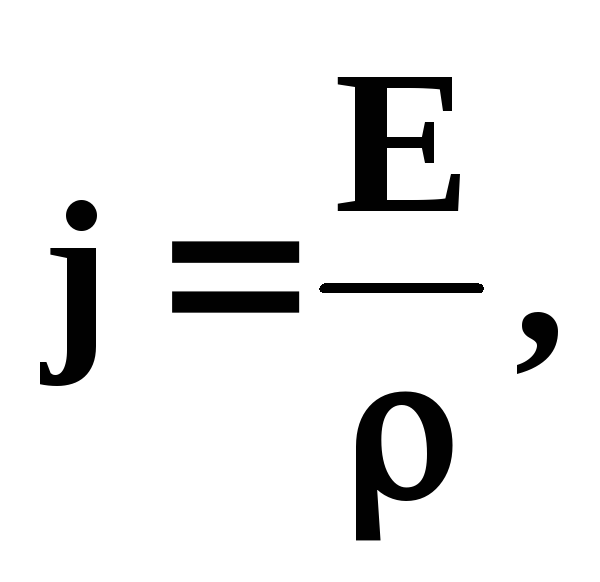
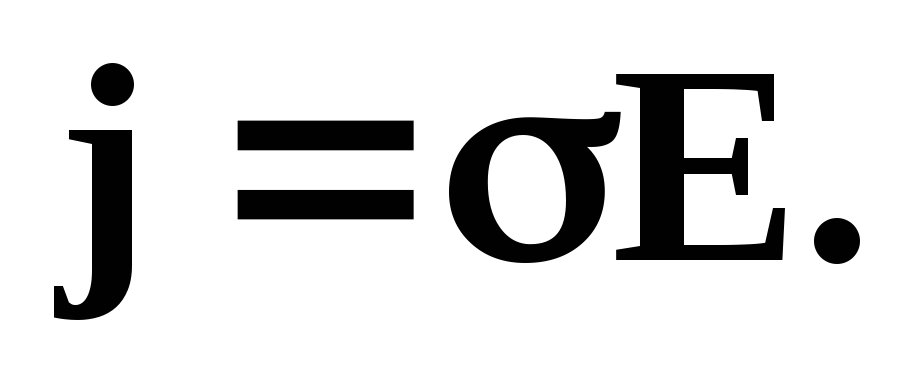
    – закон Ома в дифференциальной форме.

    3.2.3. Сторонние силы. Закон Ома для цепи, содержащей эдс

    Для возникновения и существования электрического тока необходимо:

    наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно;

    наличие электрического поля, энергия которого должна каким-то образом восполняться.

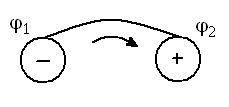
    Соединим проводником два тела с зарядами +q и –q. Кулоновские силы заставляют электроны перемещаться по проводнику. Возникнет ток. Однако тела при этом будут разряжаться, разность потенциалов уменьшится, ток быстро прекратится.

    Т.е. если в цепи действуют только силы электростатического поля, то происходит перемещение носителей таким образом, что потенциалы всех точек цепи выравниваются и электростатическое поле исчезает.

    Следовательно, поле кулоновских сил не может являться причиной постоянного электрического тока.

    Ток в проводнике нейтрализует заряды на его концах. Для поддержания постоянного тока необходимо поддерживать постоянную разность потенциалов, следовательно, разделять заряды. Электрические силы разделять заряды не могут.

    Силы, разделяющие заряды, имеют неэлектрическую природу и называются сторонними силами.

    Устройство, в котором действуют сторонние силы, называется источником тока.

    Сторонние силы заставляют заряды двигаться внутри источника тока против сил поля. Благодаря этому в цепи поддерживается постоянная разность потенциалов.

    Перемещая заряды, сторонние силы совершают работу за счет энергии, затраченной в источнике тока. Например, в электрофорной машине разделение зарядов происходит за счет механической работы, в гальваническом элементе – за счет энергии химических реакций и т.д.

    Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС).

    Обозначим 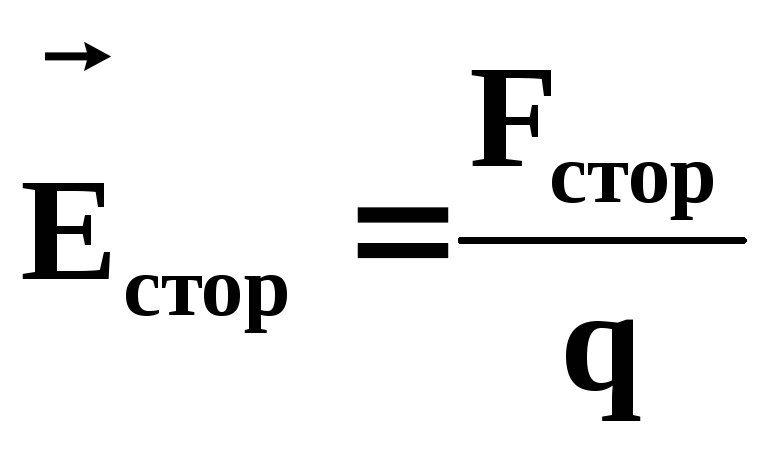— вектор напряженности поля сторонних сил.

    Результирующее поле, действующее на заряды в проводнике, в общем случае

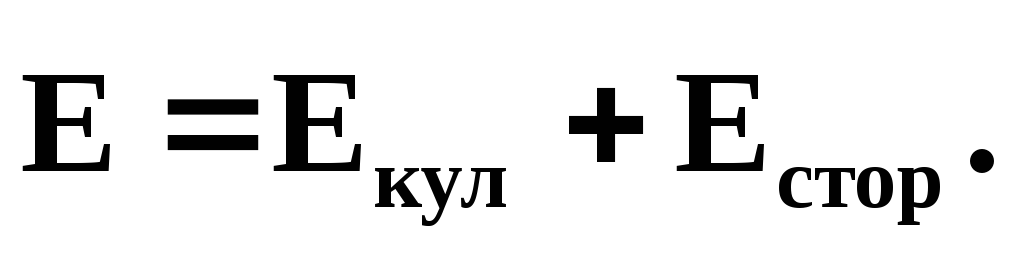
    Плотность тока в цепи

    .

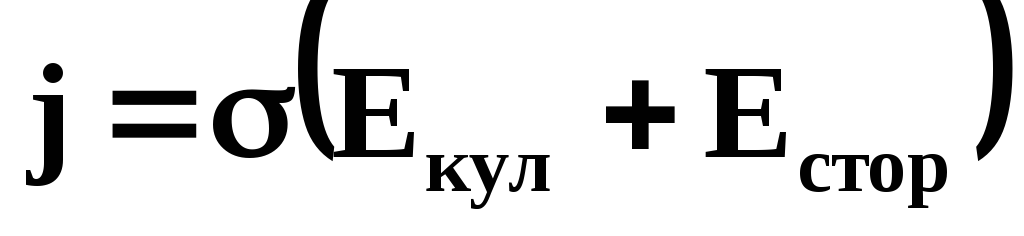    – закон Ома в дифференциальной форме для цепи, содержащей ЭДС.

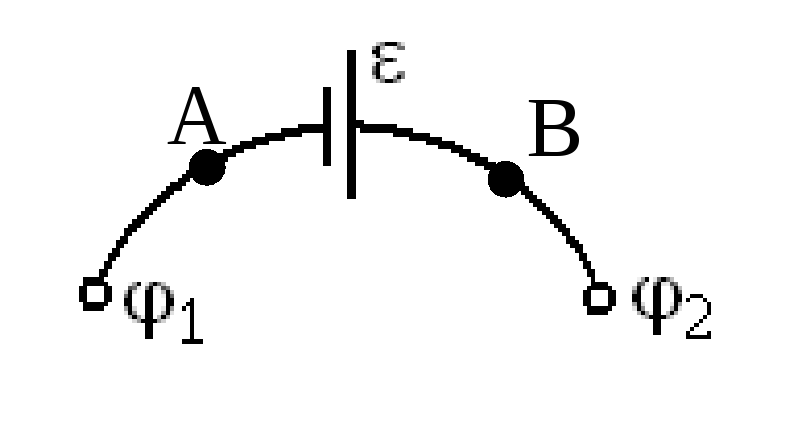
    Рассмотрим участок AB замкнутой цепи, содержащей ЭДС (рис.3.18). Выделим мысленно малый элемент dl.

    Плотность тока на этом участке опишется уравнением 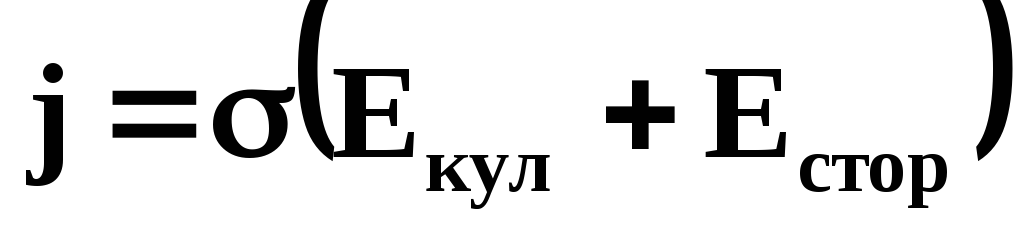. Умножим скалярно обе части этого равенства на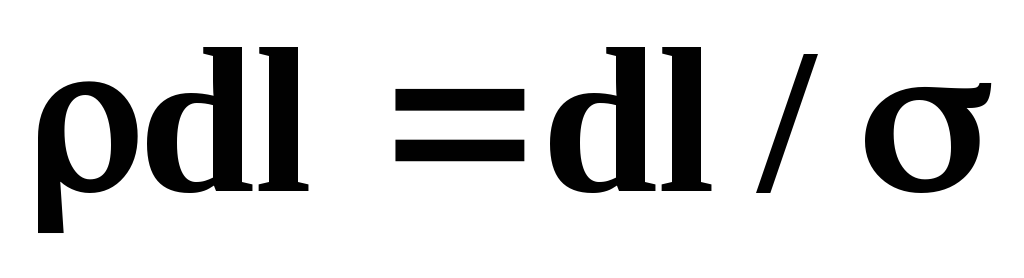и проинтегрируем по участкуAB:

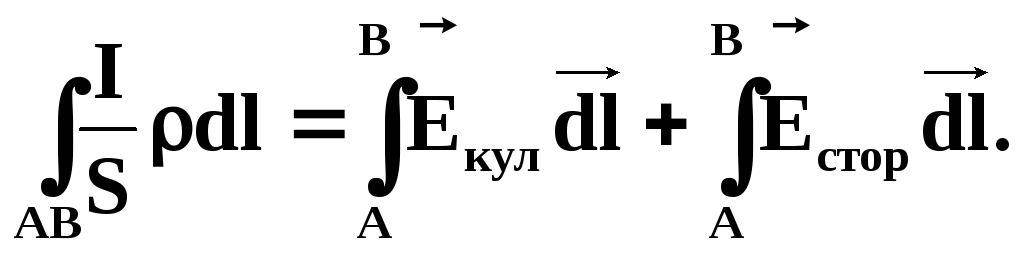
    Рассмотрим каждый интеграл в отдельности:

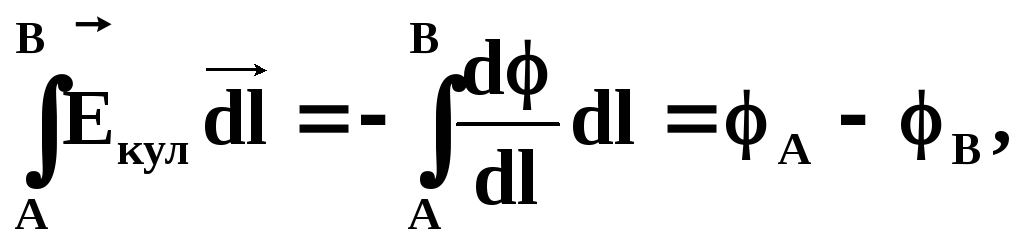
    Разность потенциалов численно равна работе кулоновских сил по перемещению единичного положительного заряда из т.A в т.B;

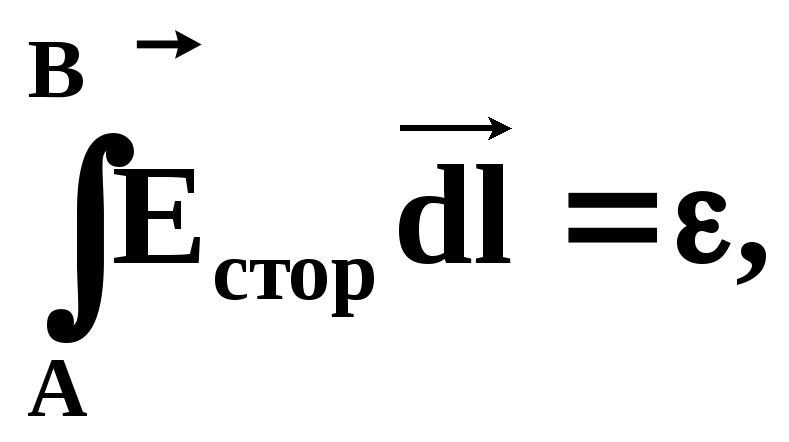
    ЭДС, действующая на участке цепи, численно равна работе сторонних сил по перемещению единичного положительного заряда из т.A в т.B;

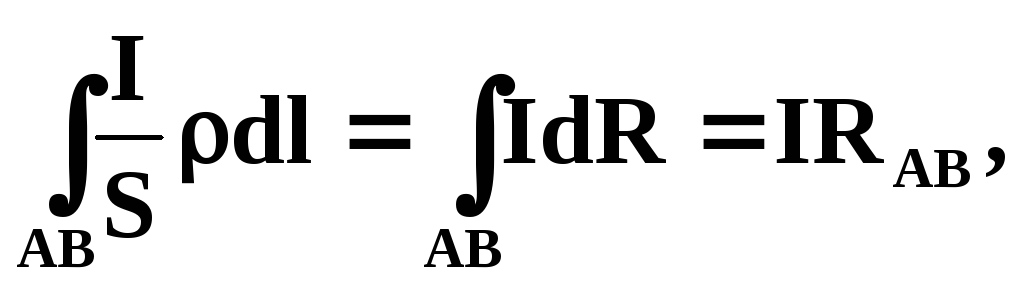
    С учетом выше сказанного можно получить:

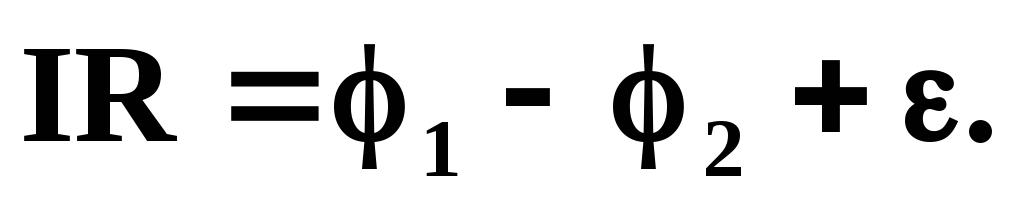
    — закон Ома для участка цепи с ЭДС.

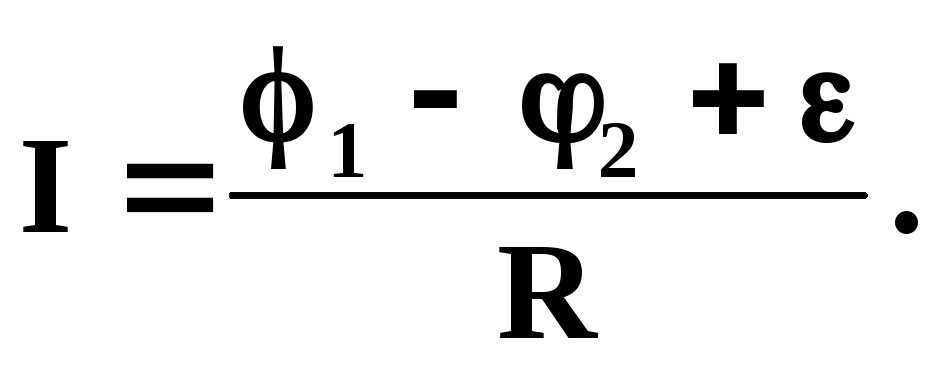
    если на данном участке цепи источник тока отсутствует, то получаем закон Ома для однородного участка цепи:

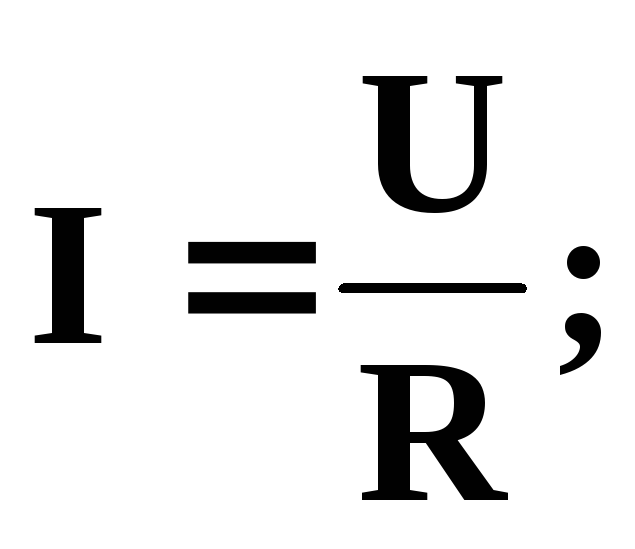
    если цепь замкнута (=0), то получим закон Ома для замкнутой цепи:

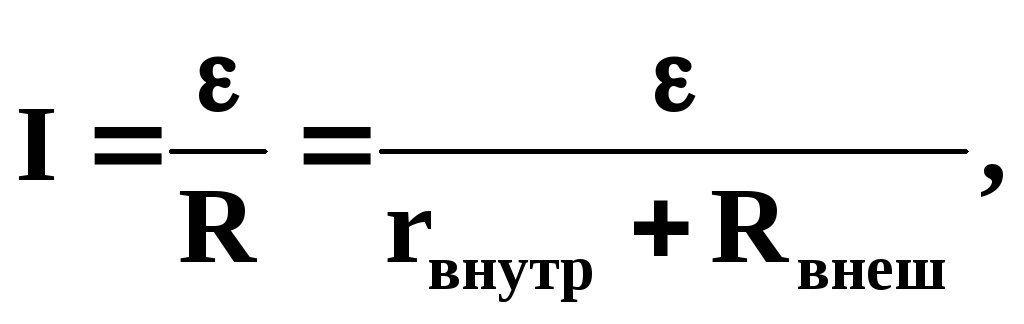
    где — ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи, rвнутр – внутреннее сопротивление источника тока, Rвнеш – сопротивление внешней цепи;

    если цепь разомкнута, то I = 0 и 12 = 2 — 1, т.е. ЭДС, действующая в разомкнутой цепи равна разности потенциалов на ее концах.

    В случае короткого замыкания сопротивление внешней цепи Rвнеш = 0 и сила тока 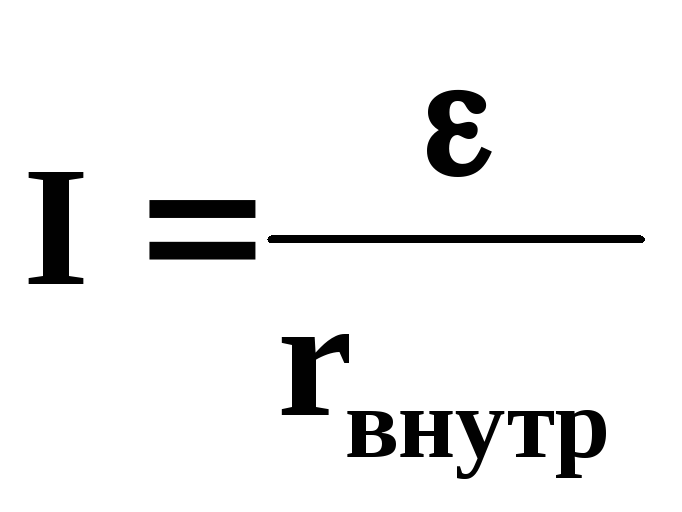в этом случае ограничивается только величиной внутреннего сопротивления источника тока.

    Падение напряжения на участке AB численно равно работе кулоновских и сторонних сил по перемещению единичного положительного заряда из т.A в т.B.

    studfiles.net