Смысл закона ома

Закон Ома для полной цепи теория и практика

Абсолютно любые потребители электрического тока (например, лампы накаливания) вместе с источником тока (ЭДС) образуют замкнутую электрическую цепь. На рисунке ниже как раз показан простейший вариант замкнутой электрической схемы, состоящая из стандартного автомобильного аккумулятора и лампочки со спиралью (представлена на рисунке в виде сопротивления).

Пусть у нас есть простая, но полная электрическая цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон Ома для полной цепи определения

Ток, следующий через нагрузку, проходит также и через собственно сам источник тока. Следовательно, протеканию тока, препятствует как собственное сопротивление проводника, так и еще внутреннее сопротивление ЕДС, например в аккумуляторной батареи это сопротивление электролита между пластинами и пограничных слоев электролита и пластин). Поэтому, общее сопротивление схемы будет складываться из двух его составляющих.

Сопротивление нагрузки (лампочки накаливания), подключенной к ЭДС, называют внешним сопротивлением, а сопротивление самого источника тока — внутренним. Внутреннее сопротивление обозначается маленькой латинской буквой r.

Если по схеме протекает ток I, то для поддержания его во внешней цепи согласно закону Ома между ее концами должна иметься разность потенциалов, равная (I*R). Но этот же ток идет и по внутренней цепи. Поэтому, для поддержания тока во внутренней части схемы, также требуется разность потенциалов между концами сопротивления r. Эта разность равна I*r. Поэтому, ЭДС аккумулятора должна иметь величину:

Из этой формулы видно, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения:

Из этой формулы:

Эти две формулы выражают закона Ома для полной цепи. В устном варианте его можно озвучит так: сила тока в любой замкнутой схеме прямо пропорциональна ЭДС и обратно пропорциональна общему сопротивлению. Повторю, что под общим сопротивлением имеется ввиду сумма внешнего и внутреннего сопротивлений.

Объяснение закона Ома для полой цепи практически ничем не отличается от объяснения закона Ома для участка цепи. Как видим из математических формул выше, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника. Кстати, о том, что такое что такое ЭДС, для тех кто забыл, можно почитать здесь:

Как понять закон Ома? Чтобы интуитивно его понять, обратимся к аналогии представления тока в виде жидкости. Именно так и рассуждал Георг Ом, когда в 1826 годупроводил опыты, благодаря которым был открыт закон Ома, кстати названный в честь его открытия.

Итак, предположим что электрический ток — это не движение элементарных частиц заряда в проводнике, а движение потока жидкости в трубе. Сначала воду необходимо поднять насосом на водокачку, оттуда, под действием потенциальной энергии, она потечет вниз и течет по трубе. Причем, чем выше насос закачает жидкость, тем быстрее вода потечет в трубе. Отсюда легко сделать вывод о том, что скорость потока воды (или сила тока в проводнике) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов — напряжение).

Таким образом, сила тока прямо пропорциональна напряжению.

Гидравлическое сопротивление — это сопротивление трубы, обусловленное ее шероховатостью и диаметром стенок. Можно предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество жидкости (больший ток) способен пройти через ее сечение. Т.о можно сказать, что сила тока обратно пропорциональна сопротивлению.

Такую условную аналогию можно использовать только для принципиального понимания работы закона Ома для полной цепи, на самом деле это довольно грубое и не точное приближение, которое, тем не менее, находит свое применение на практике.

В действительности, сопротивление вещества зависит от колебания атомов кристаллической решетки, а ток обусловлен движением свободных носителей заряда. В металлических веществах свободными носителями заряда являются электроны, сорвавшиеся со своих атомных атомных орбит.

Закон Ома для неоднородного участка цепи

Простой вариант закона Ома справедлив для так называемого однородного участка, то есть участка, на котором отсутствуют источники тока. Сейчас мы представим вывод формулы более общего соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон для полной цепи

Участок считается неоднородным, если на нём имеется собственный источник тока. Иными словами можно сказать, неоднородный участок это участок с ЭДС

На рисунке ниже изображен неоднородный участок, включающий резистор R и источник тока. ЭДС источника равна какому-то значению E его внутреннее сопротивление считаем равным нулю

Сила тока на этом участке равна I, ток следует от точки a к точке b. Причем он может быть создан не только одним лишь источником E Так как, рассматриваемый на рисунке участок, как правило, входит в состав более сложной схемы (не показанной на рисунке), а в этой сложной схеме могут иметься и другие токовые источники. Поэтому общий ток является результатом совокупного действия всех отдельных источников, имеющихся в схеме. Полный вариант текста можно скачать по зеленой ссылке чуть выше.

Итак, переходим от теории к практике. Необходимо вычислить силу тока, если известно что сопротивление равно 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

Источник ЭДС подсоединен к сопротивлению с номиналом 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Определить силу тока, зная что ЭДС источника 12 В, а внутреннее сопротивление 1,9825 Ом.

Обучающий видеофильм для закрепления полученных знаний по теме закон Ома

www.texnic.ru

Закон Ома для участка цепи

Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.

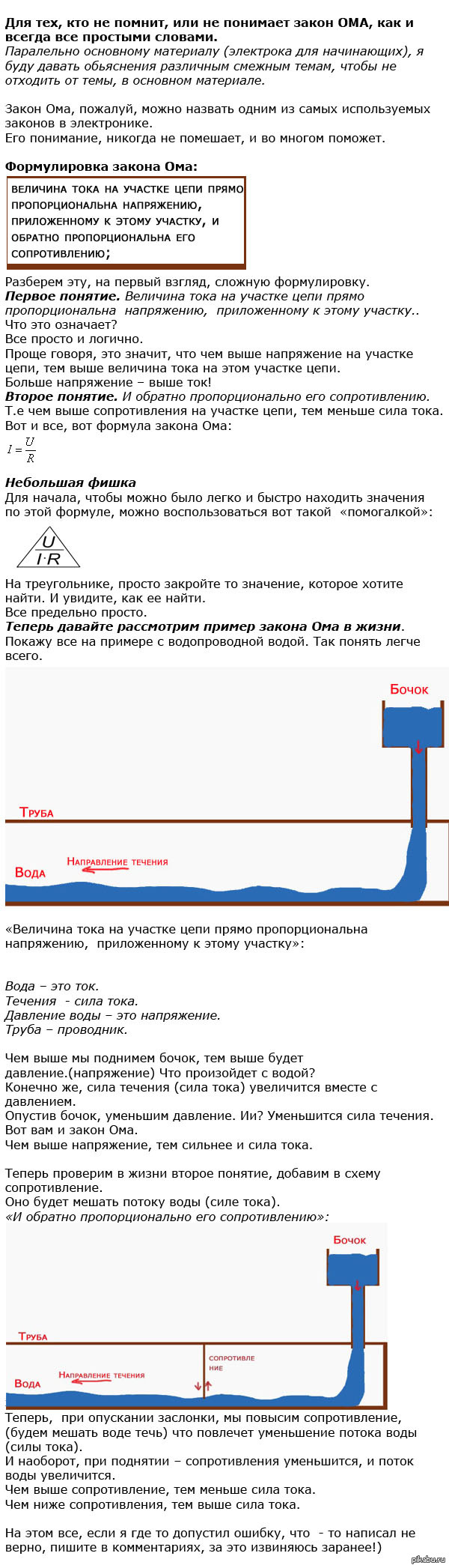
Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.

Чтобы выразить закон Ома математически наиболее просто, считают, что сопротивление проводника, в котором при напряжении 1 В проходит ток 1 А, равно 1 Ом.

Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтому закон Ома для участка цепи записывается следующей формулой:

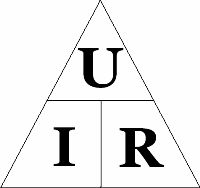
Любой участок или элемент электрической цепи можно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.

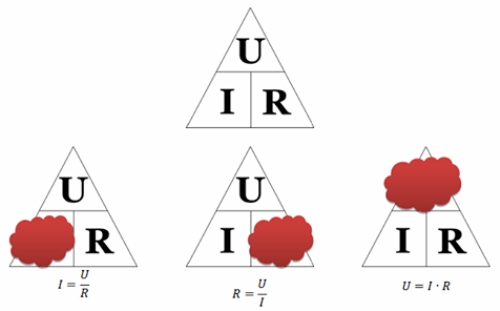
Как использовать треугольник Ома: закрываем искомую величину — два других символа дадут формулу для её вычисления. Кстати, законом Ома называется только одна формула из треугольника – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют.

Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:

Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килоомах и мегаомах соответственно.

Другие статьи про электричество в простом и доступном изложении:

Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.

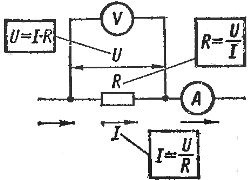
Рис 1. Применение закона Ома для участка цепи

Приведем пример расчета тока по закону Ома . Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.

Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения

Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению . Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.

Напряжение на участке цепи часто называют падением напряжения . Это нередко приводит к недоразумению. Многие думают, что падение напряжения есть какое-то потерянное ненужное напряжение. В действительности же понятия напряжение и падение напряжения равнозначны. Потери и падение напряжения — в чем различие?

Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.

Умножив I = 0,005 А на R —10 000 Ом, получим напряжение,равное 5 0 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В

В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.

По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.

Сопротивление всегда представляет собой отношение напряжения к току. Если напряжение увеличить или уменьшить в несколько раз, то ток увеличится или уменьшится в такое же число раз. Отношение напряжения к току, равное сопротивлению, остается неизменным.

Не следует понимать формулу для определения сопротивления в том смысле, что сопротивление данного проводника зависит оттока и напряжения. Известно, что оно зависит от длины, площади сечения и материала проводника. По внешнему виду формула для определения сопротивления напоминает формулу для расчета тока, но между ними имеется принципиальная разница.

Ток в данном участке цепи действительно зависит от напряжения и сопротивления и изменяется при их изменении. А сопротивление данного участка цепи является величиной постоянной, не зависящей от изменения напряжения и тока, но равной отношению этих величин.

Когда один и тот же ток проходит в двух участках цепи, а напряжения, приложенные к ним, различны, то ясно, что участок, к которому приложено большее напряжение, имеет соответственно большее сопротивление.

А если под действием одного и того же напряжения в двух разных участках цепи проходит различный ток, то меньший ток всегда будет на том участке, который имеет большее сопротивление. Все это вытекает из основной формулировки закона Ома для участка цепи, т. е. из того, что ток тем больше, чем больше напряжение и чем меньше сопротивление.

Расчет сопротивления с помощью закона Ома для участка цепи покажем на следующем примере. Пусть требуется найти сопротивление участка, через который при напряжении 40 В проходит ток 50 мА. Выразив ток в амперах, получим I = 0,05 А. Разделим 40 на 0,05 и найдем, что сопротивление составляет 800 Ом.

Закон Ома можно наглядно представить в виде так называемой вольт-амперной характеристики . Как известно, прямая пропорциональная зависимость между двумя величинами представляет собой прямую линию, проходящую через начало координат. Такую зависимость принято называть линейной .

На рис. 2 показан в качестве примера график закона Ома для участка цепи с сопротивлением 100 Ом. По горизонтальной оси отложено напряжение в вольтах, а по вертикальной оси — ток в амперах. Масштаб тока и напряжения может быть выбран каким угодно. Прямая линия проведена так, что для любой ее точки отношение напряжения к току равно 100 Ом. Например, если U = 50 В, то I = 0,5 А и R = 50 : 0,5 = 100 Ом.

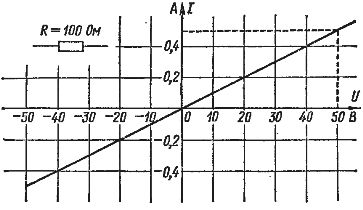
Рис. 2 . Закон Ома (вольт-амперная характеристика)

График закона Ома для отрицательных значений тока и напряжения имеет такой же вид. Это говорит о том, что ток в цепи проходит одинаково в обоих направлениях. Чем больше сопротивление, тем меньше получается ток при данном напряжении и тем более полого идет прямая.

Приборы, у которых вольт-амперная характеристика является прямой линией, проходящей через начало координат, т. е. сопротивление остается постоянным при изменении напряжения или тока, называются линейными приборами . Применяют также термины линейные цепи, линейные сопротивления.

Существуют также приборы, у которых сопротивление изменяется при изменении напряжения или тока. Тогда зависимость между током и напряжением выражается не по закону Ома, а более сложно. Для таких приборов вольт-амперная характеристика не будет прямой линией, проходящей через начало координат, а является либо кривой, либо ломаной линией. Эти приборы называются нелинейными .

electricalschool.info

Закон Ома для всей цепи

Согласно закону Ома величина тока в замкнутой цепи прямо пропорциональна э. д. с. источника электрической энергии и обратно пропорциональна сопротивлению всей цепи:

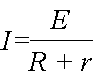
где I — величина тока, А;

Е- э. д. с. источника тока, В;

R- сопротивление внешнего участка цепи ,ом;

r- сопротивление внутреннего участка цепи, ом.

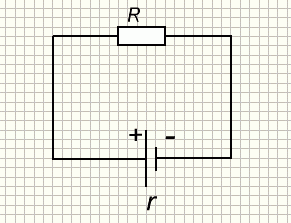
В замкнутой электрической цепи ток протекает по внешнему участку (R) и через сам источник тока, который, как и всякий проводник, обладает определенной величиной электрического сопротивления. Оно называется внутренним сопротивлением источника тока и обозначается r

Закон Ома является одним из основных законов электротехники.

Физический смысл зависимости тока от э. д. с. источника электрической энергии и сопротивления цепи заключается в том, что, чем больше э. д. с., тем больше энергия носителей зарядов, т. е. больше скорость их направленного, упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей, а следовательно, и величина тока уменьшаются.

Э. д. с. не зависит от величины тока и сопротивления, так же как величина сопротивления не может быть изменена уменьшением тока или уменьшением э. д. с. .

Э. д. с. зависит только от свойств источника тока, а сопротивление — от материала, размеров и температуры проводника.

stoom.ru

Лучшие сверху
Первые сверху
Актуальные сверху

180 комментариев

Ответьте мне, уважаемые подписчики и все кто читает эту тему, на один вопрос:
Допустим, мы взяли весы и уровняли их 2 мя сосудами, одинокого наполненными (не до полна) водой.
Далее, в один из сосудов, мы немного опустим грузик, но оставим в руке, как поведут себя весы? (и почему, по вашему мнению?)

PS. Больно много людей, не понимают зависимость давления от высоты водяного столба.. )

Можно я, можно я. =)

Сначала думал, что весы останутся в неизменном состоянии, т.к. рука удерживает перетягивает весь вес тела на себя.

Но я изменил свою точку зрения: сторона с грузом перевесит, верно? Если бы сосуд был пустой и так же держали в сосуде груз, не было б разницы, но там жидкость, которая соприкасается с грузом. Я не знаю теории, объясню свой ход мыслей своими словами: груз оказывает давление на воду, перебрасывает часть своего веса на воду, которая уже оказывает давление в итоге на сосуд, который установлен на весах —> перевешивает.

pikabu.ru

Цель работы: изучение движения зарядов внутри проводника и проверка закона Ома для проводников.

Электропроводность проводника определяется наличием в нем свободных носителей заряда (электроны в металле, положительные и отрицательные ионы в электролитах). Предположим, что носители тока слабо взаимодействуют друг с другом, а взаимодействие их с другими частицами сводится к соударениям. Кроме того, будем считать, что движение этих частиц подчиняется законам классической механики, что справедливо для полупроводников или электролитов, но не справедливо для металлов.

В отсутствие электрического поля частицы в проводнике (которые приближенно можно считать свободными) совершают хаотическое движение, сталкиваясь при этом с ионами на узлах кристаллической решетки, с атомами примесей и т.д. Все направления движения свободных частиц равноправны, и какого-нибудь потока частиц, то есть тока, не возникает. Поэтому усредненные по всему коллективу частиц проекции скорости равны нулю. Если проводник находится в электрическом поле, то на частицы действуют направленные силы. Если следить за какой-нибудь частицей, то можно обнаружить, что на тепловое хаотическое движение частицы накладывается направленное движение ее под действием силы со стороны электрического поля (так называемый дрейф).

Рассмотрим движение одной частицы. Пусть заряженная частица с зарядом е и массой m движется в однородном электрическом поле. Сила, действующая на частицу со стороны поля, равна , где – напряженность поля, которую можно считать постоянной. Тогда уравнение ее движения имеет вид:

Пусть вектор напряженности направлен по оси Ох, тогда ускорение частицы тоже направлено по этой оси и равно . Если начальная скорость частицы равна нулю, то в момент времени t она равна , а средняя скорость вдвое меньше, за некоторый промежуток времени τ она равна

Примем такую модель. Будем считать, что движущиеся заряженные частицы сталкиваются с другими частицами через одинаковое время τ, которое можно отождествить со средним временем между соударениями. Будем считать, что в среднем в результате соударения частицы останавливаются, а после этого они снова начинают движение в электрическом поле с нулевой начальной скоростью. По этой причине можно считать, что частицы движутся в электрическом поле со средней скоростью, даваемой формулой (1).

Сила тока – это заряд, переносимый движущимися частицами за единицу времени, а плотность тока равна силе тока через сечение проводника с площадью, равной единице. Найдем связь между плотностью тока и скоростью направленного движения частиц. Пусть частицы движутся влево со скоростью v (рис. 1). За время t они проходят путь, равный l = vt. Таким образом, за это время сечение S проводника пересекут только те частицы, которые отстоят от него на расстояние, меньшее или равное l, т.е. те частицы, которые находятся внутри цилиндра высотой l = vt и объема V = S(vt). Если концентрация частиц равна n, то их число в этом объеме равно N = nV = nS(vt). Пусть заряд одной частицы равен q. Тогда за время t через сечение проводника протекает суммарный заряд N частиц, равный Q = qN = qnSvt. Следовательно, сила тока через проводник равна , а плотность тока – .

В рассматриваемом нами случае вектор плотности тока направлен в направлении приложенного поля, т.е. вдоль оси Ох. Величина j пропорциональна средней скорости направленного движения, а именно j = еnavn. Подставляя сюда avn из формулы (1), получим:

Это выражение называют законом Ома в дифференциальной форме. Величина

называется коэффициентом электропроводности или просто электропроводностью данного проводника, а коэффициент пропорциональности между средней скоростью направленного движения зарядов avn и напряженностью приложенного электрического поля Е называют подвижностью носителей тока. Из формулы (2) видно, что подвижность выражается следующим образом:

Электропроводность и подвижность связаны друг с другом соотношением: s = enl.

Смысл закона Ома заключается в том, что средняя скорость направленного движения носителей тока пропорциональна напряженности электрического поля, т.е. пропорциональна действующей на частицы силе. Закон Ома выполняется для металлов, полупроводников, электролитов, т.е. для тех веществ, в которых носители тока испытывают большое число соударений. При этом данный закон выполняется при не слишком сильных полях, когда роль соударений велика. Закон Ома не выполняется при токах в вакууме, так как в этом случае носители тока практически не испытывают столкновений. Закон Ома очень ограниченно выполняется в плазме, так как в плазме обычно непостоянно число носителей тока. Отметим, что выражение для коэффициента электропроводности (3) соответствует опыту гораздо хуже, чем сам закон Ома. Это выражение более или менее применимо для полупроводников или электролитов, но совершенно не пригодно для металлов, в то время как сам закон Ома для металлов выполняется достаточно хорошо.

Обычно в физике и особенно в электротехнике применяется закон Ома в другом виде – в так называемой интегральной форме. Получим вид этого закона.

Рассмотрим участок однородного проводника, имеющего для простоты цилиндрическую форму (рис. 2). Пусть площадь поперечного сечения проводника S, а длина l. К концам проводника приложена разность потенциалов U = j₁ – j₂, то есть внутри проводника действует электрическое поле . Поэтому в проводнике возникает электрический ток, плотность тока, согласно закону Ома, j = sЕ. Если ток распределен равномерно по сечению проводника, то сила тока I = jS = sES.