С помощью правил подсчета цифр

Различают вычисления: 1) со строгим учетом погрешностей и 2) без строгого учета. В менее ответственных вычислениях с приближенными числами пользуются вторым способом, основанным на так называемых правилах подсчета цифр.

В этих правилах используют понятия: 1) десятичных знаков, 2) значащих цифр, 3) точных и сомнительных цифр.

1) Напомним, что десятичными знаками числа называют все его цифры, стоящие правее запятой. Например, числа 3,5 и 3,05 имеют соответственно один и два десятичных знака.

2) Значащими цифрами числаназывают все его цифры, начиная с первой слева отличной от нуля, кроме нулей, стоящих в конце записи числа на месте отброшенных при округлении цифр (как уже отмечалось, эти нули обычно подчеркивают или пишут меньшими).

Примеры: В числе 3,5 – две значащие цифры, в числе 0,0307 – три значащие цифры. В числе 35 000, полученном в результате округления до тысяч, две значащие цифры.

3) Если граница абсолютной погрешности приближенного числа равна половине единицы разряда последней его цифры, то все цифры этого числа называют точными. Если же эта граница больше половины единицы разряда последней цифры числа, то последняя цифра такого числа называется сомнительной.

Примеры. В числе 2,06 ( 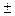0,005) цифры 2, 0 точные, а 6 — сомнительная. В числе 2,06 ( 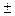0,01) цифры 2, 0 точные, а 6 — сомнительная. В числе 35000, полученном в результате округления до тысяч, цифры 3 и 5 точные, а все три нуля — сомнительные.

Правила подсчета цифр тесно связаны с принципом А.Н.Крылова (1863-1945): Приближенное число следует писать так, чтобы в нем все значащие цифры, кроме последней, были верны и лишь последняя цифра была бы сомнительна и при этом не более как на одну единицу.

Например,если приближенное число записано: х ≈ 3,72;то это значит, что оно задано с точностью до сотых, т.е. х ≈ 3,72 ( 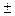0,01).Если же известно, что х ≈ 3,72 ( 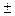0,02)то, согласно принципу А.Н. Крылова, его надо написать так: х ≈ 3,7.

Вычисления с приближенными числами, записанными таким способом, выполняют как над точными числами, но, придерживаясь таких правил.

Правила подсчета цифр.

1)При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.

Пример. Найти сумму приближенных чисел 127,42; 67,3; 0,12 и 3,03.

Решение. 127,42 +67,3+ 0,12 + 3,03= 197,87 ≈ 197,9.

Пример.Найти разностьчисел: 418,7 и 39,832.

Решение 418,7— 39,832= 378,87 ≈ 378,9.

2)При умножении и делении приближенных чисел в произведении надо сохранить столько значащих цифр, сколько их есть в данном числе с наименьшим количеством значащих цифр.

Пример. Умножить приближенные числа 3,4 и 12,32.

Решение. 3,4 х 12,32 = 41,888 ≈ 42.

Задача. Площадь прямоугольного участка приближенно равна 7,6 м 2 , ширина – 2,38 м. Чему равна его длина?

Решение. Длина равна частному от деления 7,6 на 2,38.

L = 7,6 /2,38= 3,19 ≈ 3,2 м.

Последнюю цифру частного 9 можно было и не писать, а, получив в частном две значащие цифры, заметив, что остаток больше половины делителя, округлить частное с избытком.

3) При возведении приближенных чисел в квадрат и куб в результате сохраняется столько значащих цифр, сколько их в основании.

Примеры. 2,3 2 = 5,29 ≈ 5,3. 0,8 3 = 0,512 ≈ 0,5.

4) В промежуточныхрезультатах следует брать одной цифрой больше, чем рекомендуют предыдущие правила.

5) Если некоторые данные имеют больше десятичных знаков (при действиях первой ступени) или больше значащих цифр (при действиях 2-й и 3-й ступеней), чем другие, то предварительно их следует округлить, сохраняя лишь одну запасную цифру.

6) Если данные можно брать с произвольной точностью, то для получения результата с k цифрами данные следует брать с таким числом цифр, которое даёт согласно правилам 1-4 «k + 1» цифру в результате.

Применение правил.

Применение правил подсчета цифр рассмотрим на примере.

Пример. Найти значение х = [(a – b) c]/(a + b), a ≈ 9,31; b ≈ 3,1; c ≈ 2,33.

Решение. a – b = 9,31 – 3,1 = 6,21;

(a – b) c = 6,21 х 2,33 ≈ 14,5;

a + b = 9,31 + 3,1 = 12,4;

х = 14,5 / 12,4 ≈ 1,2.

Ответ. х ≈ 1,2.

Примечание. Сформулированные ранее правила подсчета цифр имеют вероятностный смысл: они более вероятны, хотя существуют примеры, не удовлетворяющие этим правилам. Поэтому вычисления способом подсчета цифр – самый грубый способ оценки погрешности результатов действий. Однако он очень прост и удобен, а точность таких вычислений вполне достаточна для большинства технических расчетов. Поэтому этот способ широко распространен в вычислительной практике.

В более ответственных вычислениях пользуются способом границ или способом граничных погрешностей.

studopedia.ru

Правила подсчета цифр;

Правило I . При сложении и вычитании приближенных чисел в результате сохраняют цифры только тех разрядов, в кото­рых имеются верные цифры во всех исходных данных.

Правило II. При умножении и делении приближенных чисел в результате сохраняют столько значащих цифр, сколько вер­ных значащих цифр в исходном данном с наименьшим их количе­ством.

Правило III. При возведении в степень приближенного числа в результате сохраняют столько значащих цифр, сколько верных значащих цифр в возводимом в степень числе.

Правило IV. При извлечении корня любой степени из приближенного числа в результате сохраняют столько значащих цифр, сколько верных значащих цифр в подкоренном числе.

Правило V. При нахождении десятичного логарифма при­ближенного числа в мантиссе (независимо от характеристики) со­храняют столько значащих цифр, сколько верных значащих цифр в самом числе.

Правило VI. При нахождении значения тригонометриче­ской функции в результате сохраняют две значащие цифры, если угол задан с точностью до градуса, и четыре значащие цифры, если угол задан с точностью до минут.

Правило VII. Если конечный результат нужно получить с некоторой точностью, то во всех исходных данных необходимо иметь столько верных значащих цифр, сколько требуется для полу­чения результата с одной лишней цифрой. В конечном результате эта лишняя цифра отбрасывается.

Правило VIII. Если значения отдельных исходных дан­ных имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень и извлечении корня), чем другие, то их предварительно округляют, сохранив только одну лишнюю цифру.

Алгоритмы измерений и обработки полученных результатов. Прямые измерения. Метод среднего арифметического.

1. Проводят несколько измерений искомой величины x (при неизменных условиях опыта).

2. Определяют наиболее достоверное значение измеряемой величины:

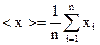
3.Вычисляют модули отклонения каждого результата от сред­него:

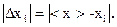
4. Определяют среднюю абсолютную погрешность:

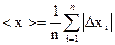
5. Оценивают случайную погрешность:

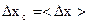при n ≥ 10

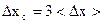при n = 5

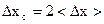при n = 7;8.

6. Оценивают инструментальную погрешность:

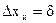или (или ).

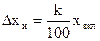7. Оценивают погрешность отсчета:

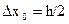
8. Оценивают погрешность вычисления:

.

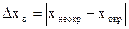9. Оценивают полную погрешность:

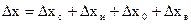
10. Оценивают относительную погрешность:

%.

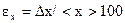11. Учитывают поправку на систематическую погрешность:

.

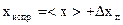12. Результат измерения записывают в интервальной форме:

.

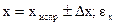Оценка погрешности косвенно измеряемой величины

(дифференциальный метод границ погрешностей)

Рассмотрим сначала простейший случай, когда функция у за­висит только от одного аргумента х, т.е.

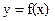(1)

Величина х измеряется прямым методом, а у косвенным: вы­числяется по формуле (1). Если величина х измерена с абсолютной погрешностью 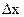, то величина у также будет определена с некото­рой погрешностью 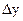. При малых погрешностях 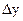= tgα·Δх, где α – угол между касательной к кривой у = f(х) и осью абсцисс. Но тангенс угла наклона касательной к оси абсцисс равен производной от функции у в соответствующей точке, т.е. tgα = у’. Поэтому

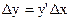(2)

Поскольку значение у’ может быть отрицательным, а абсо­лютная погрешность 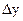всегда положительна, в соотношении (2) производную 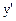нужно заменить ее модулем :

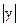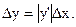(3)

Таким образом, чтобы вычислить абсолютную погрешность 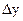косвенно измеряемой величины у, нужно абсолютную погрешность 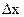величины, измеренной прямым методом, умножить на модуль производной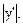

Значение производной у’ должно вычисляться при истинном значении x, т.е. при x = х_ист. Но оно экспериментатору не известно. По этой причине на практике 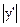приходится вычислять при х = x_изм. Такое приближение оправдано тем, что обычно погрешно­сти измерений не очень велики.

Теперь рассмотрим случай, когда у зависит от нескольких ар­гументов: у = f(x₁,x₂,…,x_N). Все величины х_i, (i == 1, 2. N) изме­ряются независимыми прямыми методами, а у – косвенным. Пусть абсолютные погрешности прямых измерений соответственно равны 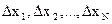. Это приведет к погрешности 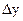. Если бы при пря­мых измерениях с некоторой погрешностью была определена толь­ко одна величина х₁, а остальные x₂,x₃,…,x_N были бы найдены точно, то в соответствии с формулой (3) абсолютная погрешность косвенно измеряемой величины была бы равна

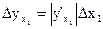(4)

где 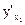– частная производная от функции у по аргументу х₁ .т.е. производная от у по х₁ в предположении, что все остальные аргу­менты (х₂,х₃. x_N) постоянные, 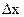– абсолютная погрешность из­мерения x₁.

Рассуждая аналогично относительно других величин х_i, (i = 2, 3. N), приходим к выводу, что каждая погрешность 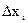, вносит свой вклад в погрешность величины у, которую можно оценить по формуле

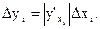(5)

Тогда общая погрешность 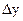, обусловленная неточным изме­рением всех аргументов х_i, будет равна сумме соответствующих ча­стных погрешностей (5):

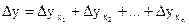(6)

В формуле (6) суммирование проводится потому, что под 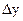понимается максимальная абсолютная погрешность, т.е. ее верхняя граница, что осуществляется тогда, когда все погрешности 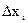, вы­зывают отклонение величины у в одну сторону, например, в сторо­ну ее завышения.

Подставив в равенство (6) значение всех слагаемых, найден­ных в формуле (5), получим

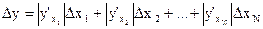. (7)

Эта формула является основной для определения абсолютной погрешности косвенно измеряемой величины у.

studopedia.su

Правило подсчета цифр это

Раздел 1. Приближенные числа и действия над ними

1.1 Виды погрешностей при приближенных вычислениях

Точное решение некоторых математических задач невозможно получить классическими методами, или это решение может быть получено в таком сложном виде, что неприемлемо для дальнейшего практического использования. Кроме того, точное решение задачи может потребовать очень большого количества (от нескольких десятков до многих миллиардов) действий. В таких случаях прибегают к приближенным и численным методам решения.

Появление компьютеров значительно расширило область применения этих методов. В настоящее время трудно себе представить инженера, не владеющего компьютером и методами приближённых вычислений.

Заметим, что любой компьютер способен запоминать большие, но конечные массивы чисел и производить над ними арифметические операции и сравнения с большой, но конечной скоростью. То есть машина способна выполнять очень большое, но конечное число операций. Поэтому при работе на компьютере можно использовать только те математические модели, которые описываются конечным набором чисел, и использовать только конечные последовательности арифметических действий.

Математическими моделями различных явлений служат функции, производные, интегралы, дифференциальные уравнения и т.п. При работе на компьютере эти исходные модели следует заменить такими, которые описываются конечными наборами чисел с указанием конечной последовательности действий для их обработки. Для этого функцию заменяют таблицей, определённый интеграл — суммой и т.д. Кроме того, вычислительная машина обладает конечной памятью и может оперировать с числами конечной длины, поэтому промежуточные результаты округляются. В результате этого даже точный метод с конечным числом действий становится приближенным.

Таким образом, решение, полученное численным методом, является приближенным.

Причинами появления погрешностей являются:

• Несоответствие математической модели изучаемому реальному явлению
• Погрешность исходных данных.
• Погрешность метода решения.
• Погрешности округлений в арифметических и других действиях над числами.

Погрешность решения, вызванная первыми двумя причинами, называется неустранимой — она не зависит от математика.

Погрешность метода возникает потому, что численным методом, как правило, решается не исходная задача, а более простая. Кроме того, обычно численный метод основан на бесконечном процессе, который приходится обрывать на некотором шаге.

Большинство численных методов зависит от одного или от нескольких параметров. Выбор параметров метода позволяет регулировать погрешность метода.

Погрешность округлений не должна быть существенно больше погрешности метода. А погрешность метода целесообразно выбирать в 2-5 раз меньше неустранимой погрешности.

1.2 Приближенные числа

На практике часто приходится иметь дело с числами, которые выражают истинную величину не точно, а приблизительно. Такие числа называются приближенными .

Обозначим точное числовое значение некоторой величины a , приближённое числовое значение этой же величины a * . Тогда a » a * .

Заменяя точное число a приближенным числом a * , мы совершаем ошибку (погрешность).

Определение 1.1. Абсолютной погрешностью приближенного числа a * называется абсолютная величина разности между этим числом и его точным значением | a — a * | .

Поскольку точное значение величины обычно бывает неизвестно, то невозможно вычислить и абсолютную погрешность. Но можно указать положительное число D ( a * ) , удовлетворяющее неравенству:

hm.tpu.ru

Приближенные вычисления

1.6.1 Правило подсчета цифр.

Различают приближенные вычисле­ния со строгим учетом погрешностей и без строгого учета. В менее ответственных вычислениях с приближенными числами пользуются вторым способом, основанным на так называемых правилах подсчета цифр. В этих правилах используются понятия десятичных знаков, значащих, точных и сомнительных цифр. Напомним, что десятичными знаками числа называют все, его цифры, стоящие правее запятой. Например, числа 3,5 и 3,05 имеют соответственно один и два десятичных знака. Значащими цифрами числа называются все его цифры, начиная с отличной от нуля первой слева, кроме нулей, стоящих в конце записи числа на месте отброшенных при округлении цифр (эти нули обычно подчеркивают или пишут меньшими, также можно поступать и с добавленными неверными знаками).

Пример. В числе 3,5 — две значащие цифры, в числе 0,0307— три значащие цифры. В числе 35000, полученном в результате округле­ния до тысяч, две значащие цифры.

Если граница абсолютной погрешности приближенного числа равна половине единицы разряда последней его цифры, то все цифры этого числа называют точными. Если же эта граница больше половины единицы разряда последней цифры числа, то последняя цифра такого числа называется сомнительной.

Пример. В числе 2,06±0,005 цифры 2, 0, 6 точные. В числе 2,06±0,01 цифры 2 и 0 точные, а 6—сомнительная. В числе 35000, полученном в результате округления до тысяч, цифры 3 и 5 точные, а все три нуля — сомнительные.

Вычисления с приближенными числами, записанными таким спо­собом, выполняют, как над точными числами, но, придерживаясь следующих правил.

Правило 1. При сложении и вычитания приближен­ных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном, данном с наименьшим числом десятичных знаков.

Пример. Найти сумму приближенных чисел 127,42; 67,3; 0,12 и 3,03.

Правило 2. При умножении и делении приближенных чисел в произведении надо сохранить столько значащих цифр, сколько, их есть в данном числе с наименьшим количеством значащих цифр.

Пример. Умножить приближенные числа 3,4 и 12,32

Задача. Теплота реакции горения приближенно равна 7,6 кДж, количество вещества — 0,38 моль.Чему равна молярная теплота сгорания?

Молярная теплота сгорания равна частному от деления 7,6 на 0,38. Действие деления выполняют так: если числа не делятся на цело, то делят до следующего знака превышающего число наименьших значащих цифр и заканчивают деление, округляя последний знак, если числа делятся нацело, то округляют следующий за значащей цифрой знак.

Правило 3. При возведении приближенных чисел в квадрат и куб в результате сохраняется столько значащих цифр, сколько их в основании.

Примеры. 2,3 2 = 5,29 »5,3; 0,8 3 = 0,512 » 0,5.

Правило 4. В промежуточных вычислениях результатах следует брать одной цифрой больше, чем рекомендуют предыдущие правила, а округление производить после окончания вычислений.

Правило 5. Если данные можно брать с произвольной точностью, то для получения результата с n цифрами данные следует брать с таким чис­лом цифр, которое дает согласно перечисленным правилам n + 1 цифр в результате.

Сформулированные выше правила подсчета цифр имеют вероятностный смысл: они наиболее вероятны, хотя суще­ствуют примеры, не удовлетворяющие этим правилам. Поэтому вычис­ления способом подсчета цифр — самый грубый способ оценки погреш­ности результата действий. Однако он очень прост и удобен, а точность таких вычислений вполне достаточна для большинства технических расчетов. Поэтому этот способ широко распространен в вычислительной практике.

В ответственных вычислениях пользуются способом границ или способом граничных погрешностей, а также логарифмическим методом.

1.6.2 Приближенные вычисления по способу границ

Наилучшим в смысле строгости из известных способов приближен­ных вычислений является способ границ. Пользуясь этим способом, по известным нижним и верхним границам данных чисел находят от­дельно нижнюю и верхнюю границы результата. Вообще, нижняя граница суммы приближенных чисел равна сумме нижних границ слагаемых, а верхняя — сумме верхних границ сла­гаемых. Символически это можно записать так:

НГ(х + у) = НГх + НГу; ВГ(х + у) = ВГх + ВГу.

Аналогичные правила справедливы для умножения:

НГ(х×у) = НГх • НГу; ВГ (х×у) = ВГх • ВГу.

Для обратных действий — вычитания и деления — соответствую­щие правила имеют вид:

НГ(х — у) = НГх — ВГу;

ВГ(х — у) = ВГх — НГу;

Из определения НГ и ВГ вытекают также следующие правила:

1) округлять НГ можно только по недостатку, а ВГ — по избытку;

2) чем меньше разность ВГх — НГх, тем точнее опреде­ляется х;

3) в качестве приближенного значения хрекомендуется брать среднее арифметическое чисел НГх и ВГх; или число, близкое к нему.

Применение способа границ при вычислениях рассмотрим на примере: , если а»9,21 (±0,01), б»3,05 (±0,02), с»2,33 (±0,01).

Определяем НГ и ВГ каждого из чисел а, 6, с и, выполнив над ними соответствующие действия, находим НГ и ВГ числа х. Запись удобно оформить в виде таблицы.

studopedia.org

ШВЕЦОВ К.И., БЕВЗ Г.П.
СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ
АРИФМЕТИКА, АЛГЕБРА, 1965

Вычисления с приближенными числами, записанными таким способом, выполняют как и над точными числами, но, придерживаясь таких правил.

2. Правила подсчета цифр.

I. При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.

Пример. Найти сумму приближенных чисел 127; 42; 67; 3; 0,12 и 3,03.

Пример. Найти разность чисел: 418,7 — 39,832

II. При умножении и делении приближенных чисел в произведении надо сохранить столько значащих цифр, сколько их есть е данном числе с наименьшим количеством значащих цифр.

Пример. Умножить приближенные числа 3,4 и 12,32.

Задача. Площадь прямоугольной грядки приближенно равна 7,6 кв. м, ширина -2,38 м. Чему равна ее длина?

Решение. Длина грядки равна частному от деления 7,6 на 2,38.

Действие деления выполняют так:

Последнюю цифру частного 9 можно было и не писать, а, получив в частном две значащие цифры, заметив, что остаток больший половины делителя, округлить частное с избытком.

III. При возведении приближенных чисел в квадрат, и куб в результате сохраняется столько значащих цифр, сколько их в основании.

IV. В промежуточных результатах следует брать одной цифрой больше, чем рекомендуют предыдущие правила.

V. Если некоторые данные имеют больше десятичных знаков (при действиях первой ступени) или больше значащих цифр (при действиях II и III ступеней), чем другие, то их предварительно следует округлить, сохраняя лишь одну запасную цифру.

VI. Если данные можно брать с произвольной точностью, то для получения результата с k цифрами данные следует брать с таким числом цифр, которое дает согласно правилам I — IV k + 1 цифру в результате.

3. Применение правил. Применение вычислений способом подсчета цифр рассмотрим на примере.

Пример. Найти значение , если а ≈ 9,31, b ≈ 3,1, с ≈ 2,33.

х = 14,5 : 12,4 ≈ 1,2.

Примечание. Сформулированные выше правила подсчета цифр имеют вероятностный смысл: они наиболее вероятны, хотя существуют примеры, не удовлетворяющие этим правилам. Поэтому вычисления способом подсчета цифр — самый грубый способ оценки погрешности результатов действий. Однако он очень прост и удобен, а точность таких вычислений вполне достаточна для большинства технических расчетов. Поэтому этот способ широко распространен в вычислительной практике.

В более ответственных вычислениях пользуются способом границ или способом граничных погрешностей.

wap.cartalana.org