Правила задач на проценты

Задача 1. Вода составляет 76% картофеля. Сколько килограммов воды в 35 кг картофеля?

Решение. Вода составляет 76% от 35 кг. По правилу нахождения процентов от данного числа (чтобы найти проценты от данного числа нужно обратить проценты в десятичную или обыкновенную дробь, а затем умножить данное число на эту дробь) получаем 0,76∙35=26,6 кг.

Ответ : в 35 кг картофеля содержится 26,6 кг воды.

Задача 2. В классе 28 учеников. 75% из них занимаются спортом. Сколько учеников в классе занимаются спортом?

Решение. Так как 75%=0,75, то умножая число 28 на дробь 0,75 получаем: 0,75·28=21.

Получается, что 21 человек посещает спортивные кружки.

Ответ : 21 ученик в классе занимается спортом.

Задача 3. В классе 20 человек. Контрольную работу по математике 25% учащихся написали на «5», 35 % написали на «4», 10% всех учащихся получили «2». Сколько пятерок, четверок, троек и двоек получил класс?

Решение. Количество пятерок составляет 25% от 20. По правилу нахождения процентов от данного числа это 0,25∙20=5 учащихся. Четверки получили 35% от 20. Это 0,35∙20=7 учащихся. Двоек 10%. Это 1/10 часть от 20 учащихся, т.е. 2 человека. Остальные учащиеся получили оценку «3». Их 20-5-7-2=6 человек.

Ответ: оценку «5» получило 5 учащихся; оценку «4» получили 7 учащихся; оценку «3» получило 6 учащихся и оценку «2» получили 2 ученика.

Задача 4. В школьной библиотеке 5780 учебников, что составляет 85% всех книг, имеющихся в библиотеке. Сколько всего книг в школьной библиотеке?

Решение. Потребуется найти число по его процентам. Применяем правило нахождения числа по его процентам (чтобы найти число по его процентам нужно обратить проценты в десятичную дробь, а затем разделить данное число на эту дробь). 1) 85%=0,85; 2) 5780:0,85=578000:85=6800 книг.

Ответ: всего в библиотеке 6800 книг.

Задача 5. Токарю нужно было сделать 120 деталей, но он перевыполнил план на 10%. Сколько деталей изготовил токарь?

Решение. 10% от 120 деталей – это одна десятая часть от 120, т.е. это 12 деталей. Токарь изготовил 120+12=132 детали.

Ответ: 132 детали изготовил токарь.

Задача 6. Фирма платит рекламным агентам 5% от стоимости заказа. На какую сумму нужно выполнить заказ, чтобы заработать 2000 рублей?

Решение. 2000 рублей – это 5% от заказа. Число (все его 100%) по его процентам мы найдем по правилу нахождения числа по его процентам. Обращаем 5% в десятичную дробь и делим 2000 на эту дробь. 1) 5%=0,05; 2) 2000:0,05=200000:5=40000.

Ответ: заказ должен быть на сумму 40000 рублей.

Задача 7. После уценки на 10% цена холодильника стала 11430 рублей. Какова была цена холодильника до уценки?

Решение. Имеем: 11430 рублей – это 90% от начальной цены холодильника. Находим число по его процентам. 1) 90%=0,9; 2) 11430:0,9=114300:9=12700 рублей.

Ответ: до уценки холодильник стоил 12700 рублей.

Задача 8. Сколько процентов число 36 составляет от 48?

Решение. По соответствующему правилу: чтобы найти, сколько процентов составляет первое число от второго нужно первое число разделить на второе и результат умножить на 100% — записываем:

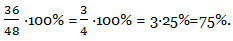
Ответ: 75% составляет число 36 от числа 48.

Задача 9. За 1 час станок-автомат изготовлял 240 деталей. После реконструкции этого станка он стал изготовлять в час 288 таких же деталей. На сколько процентов повысилась производительность станка?

Решение. Производительность станка повысилась на 288-240=48 деталей в час. Нужно узнать, сколько процентов от 240 деталей составляют 48 деталей. Для того чтобы узнать, сколько процентов число 48 составляет от числа 240 нужно число 48 разделить на 240 и результат умножить на 100%.

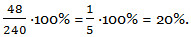
Ответ : производительность станка повысилась на 20%.

Тест 5.8.2. Задачи на проценты. Углы. Круговые диаграммы

Математика. 5 класс. Тест 8. Вариант 2.

1. В школьной библиотеке 3400 книг, из них 2890 учебников. Сколько процентов всех книг составляют учебники?

А) 70%; B) 75%; C) 90%; D) 80%; E) 85%.

2. Автотуристы в первый день проехали 36% всего пути, во второй день 39% всего пути, а в третий день — оставшиеся 200 км. Каков весь путь?

А) 700 км; В) 600 км; С) 800 км; D) 1000 км; Е) 900 км.

3. . на которые точка разбивает прямую, называются дополнительными лучами.

А) отрезки; В) прямые; С) фигуры; D) лучи; Е) стороны.

4. Найти градусные меры / ABC и / MNK.

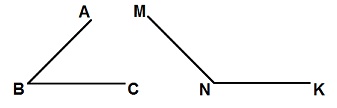А) / ABC=135°, / MNK=45°;

B) / ABC=120°, / MNK=45°;

C) / ABC=105°, / MNK=135°;

D) / ABC=45°, / MNK=135°;

E) / ABC=60°, / MNK=135°.

5. Угол АОВ равен 87°. Внутри этого угла проведен луч ОС. Найдите градусную меру угла АОС, если / ВОС=61°.

А) 36°; В) 31°; С) 26°; D) 16°; E) 158°.

6. Решить задачу, составив уравнение. Угол МОК равен 120°. Внутри этого угла проведен луч OD. Угол MOD больше угла DOK на 50°. Сколько градусов содержит угол DOK?

A) 35°; B) 85°; C) 45°; D) 60°; E) 70°.

7. . угол равен половине развернутого угла.

А) тупой; В) острый; С) любой; D) полный; Е) прямой.

8. Сколько градусов содержит угол, если он составляет 3/5 развернутого угла?

А) 45°; В) 72°; С) 135°; D) 120°; Е) 108°.

9. Сколько градусов составляет угол, если он равен 7/15 прямого угла?

А) 54°; В) 36°; С) 60°; D) 42°; Е) 66°.

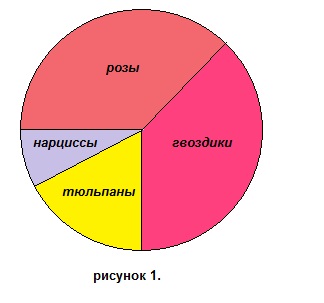10. Определить по круговой диаграмме, изображенной на рисунке 1, процентное содержание гвоздик в цветнике. Результат округлить до целых.

А) 38 %;

В) 44%;

С) 17%;

D) 8 %;

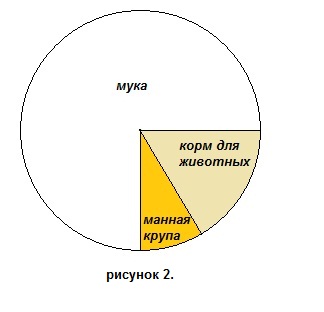11. Используя круговую диаграмму, приведенную на рисунке 2, найти процентное количество корма для животных, получающегося в результате помола пшеницы. Округлить до целых.

А) 4 %;

В) 17 %;

С) 25 %;

D) 80 %;

Е) 60 %.

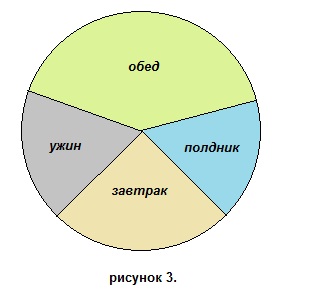12. Используя круговую диаграмму, приведенную на рисунке 3, найти в процентах норму пищи, рекомендуемую к употреблению за завтраком. Округлить до целых.

А) 17 %;

В) 10 %;

С) 45 %;

D) 35 %;

Е) 25 %.

Ответы к тестам Вы найдете на странице «Ответы« .

Нужно учиться решать задачи на проценты, так как тема «Проценты» уже никогда не закончится! Приобретайте лучшее наглядное пособие «Как решать задачи на проценты». В электронной книге не только правила и текстовые объяснения, но и обучающие видео (круговым диаграммам в книге также нашлось место!) Посмотреть подробнее можно здесь!

5.6.1. Проценты

Тема «Проценты» станет понятнее с книгой «Как решать задачи на проценты»! Узнать подробнее здесь!

Процентом называется одна сотая часть.
Чтобы выразить проценты дробью или натуральным числом, нужно число процентов разделить на 100%. (4%=0,04; 32%=0,32).
Чтобы выразить число в процентах, нужно его умножить на 100%. (0,65=0,65·100%=65%; 1,5=1,5·100%=150%).
Чтобы найти проценты от числа, нужно выразить проценты обыкновенной или десятичной дробью и умножить полученную дробь на данное число.
Чтобы найти число по его процентам, нужно выразить проценты обыкновенной или десятичной дробью и разделить на эту дробь данное число.
Чтобы найти, сколько процентов составляет первое число от второго, нужно разделить первое число на второе и результат умножить на 100%.

Пример 1. Выразить проценты дробью или натуральным числом: 130%, 65%, 4%, 200%.

130%=130%:100%=130:100=1,3;
65%=65%:100%=65:100=0,65;
4%=4%:100%=4:100=0,04;
200%=200%:100%=200:100=2.

Пример 2. Записать следующие числа в виде процентов: 1; 1,5; 0,4; 0,03.

1=1·100%=100%;
1,5=1,5·100%=150%;
0,4=0,4·100%=40%;
0,03=0,03·100%=3%.
Пример 3. Найти 15% от числа 400.

Пример 4. Найти число, если 18% его равны 900.

Пример 5. Определить, сколько процентов составляет число 320 от числа 1600.

www.mathematics-repetition.com

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Проценты в математике.

Что такое проценты в математике? Как решать задачи на проценты? Эти вопросы всплывают, увы, внезапно… Когда выпускник читает задание ЕГЭ. И ставят его в тупик. А зря. Это очень простые понятия.

Единственно, что нужно запомнить железно – что такое один процент. Это понятие — и есть главный ключ к решению задач на проценты, да и к работе с процентами вообще.

Один процент – это одна сотая часть какого-то числа. И всё. Нет больше никаких мудростей.

Резонный вопрос – а сотая часть какого числа? А вот того числа, о котором идёт речь в задании. Если там говорится о цене, один процент – это одна сотая часть цены. Если о скорости, один процент – это одна сотая часть скорости. И так далее. Понятно, что само число, о котором идёт речь, составляет всегда 100%. А если нет самого числа, то и проценты смысла не имеют…

Другое дело, что в сложных задачах само число так запрячут, что и не найдёшь. Но мы на сложное пока не замахиваемся. Разбираемся с процентами в математике.

Я не зря акцентирую слова один процент, одна сотая. Запомнив, что такое один процент, вы легко найдёте и два процента, и тридцать четыре, и семнадцать, и сто двадцать шесть! Сколько надо, столько и найдёте.

А это, между прочим, основное умение для решения задач на проценты.

Давайте найдём 3% от 400. Сначала найдём один процент. Это будет одна сотая, т.е. 400/100 = 4. Один процент – это 4. А нам сколько процентов надо? Три. Вот и умножаем 4 на три. Получим 12. Всё. Три процента от 400 – это 12.

5% от 20 это будет 20 поделить на 100 (одна сотая – 1%), и умножить на пять (5%):

5% от 20 это будет 1. Всё.

Проще некуда. Давайте-ка быстро, пока не забылось, потренируемся!

Найдите, сколько будет:
5% от 200 рублей.
8% от 350 километров.
120% от 10 литров.
15% от 60 градусов.
4% отличников от 25 учащихся.
10% двоечников из 20 человек.

Ответы (в полном беспорядке): 9, 10, 2, 1, 28, 12.

Эти числа – количество рублей, градусов, учеников и т.д. Я не написал, сколько чего, чтобы решать интересней было…

А если нам нужно записать х% от какого-то числа, например, от 50? Да всё то же самое. Один процент от 50 – это сколько? Правильно, 50/100 = 0,5. А у нас этих процентов – х. Ну и умножим 0,5 на х! Получим, что х% от 50 это – 0,5х.

Надеюсь, что такое проценты в математике вы уяснили. И легко сможете найти любое количество процентов от любого числа. Это просто. Вам сейчас по силам примерно 60% от всех задач на проценты! Уже больше половины. Ну что, добиваем оставшееся? Ладно, как скажете!

В задачах на проценты частенько встречаются обратная ситуация. Нам дают величины (какие угодно), а надо найти проценты. Освоим и этот нехитрый процесс.

3 человека из 120 – это сколько процентов? Не знаете? Ну, тогда, пусть это будет х процентов.

Вычислим х% от 120 человек. В человеках. Это мы умеем. 120 делим на 100 (вычисляем 1%) и умножаем на х (вычисляем х%). Получаем 1,2х.

х процентов от 120 человек, это 1,2х человек. А таких человек у нас три. Остаётся приравнять:

Вспоминаем, что за икс мы брали количество процентов. Значит 3 человека от 120 человек – это 2,5%.

Можно и по-другому. Обойтись простой смекалкой, безо всяких уравнений. Соображаем, во сколько раз 3 человека меньше 120? Делим 120 на 3 и получаем 40. Значит, 3 меньше 120 в 40 раз.

Искомое количество людей в процентах будет во столько же раз меньше 100%. Ведь 120 человек – это и есть 100%. Делим 100 на 40, 100/40 = 2,5

Вот и всё. Получили 2,5%.

Есть ещё способ пропорций, но это, в сущности, то же самое в сокращенном варианте. Все эти способы – правильные. Как вам удобнее, привычнее, понятнее – так и считайте.

Посчитайте, сколько процентов составляют:
3 человека из 12.
10 рублей от 800.
4 учебника из 160 книг.
24 правильных ответа на 32 вопроса.
2 угаданных ответа на 32 вопроса.
9 попаданий из 10 выстрелов.

Ответы (в беспорядке): 75%, 25%, 90%, 1,25%, 2,5%, 6,25%.

В процессе вычислений вы вполне можете столкнуться с дробями. В том числе и неудобными, типа 1,333333… А кто вам велел калькулятором пользоваться? Сами? Не надо. Считайте без калькулятора, как написано в теме «Дроби». Проценты всякие бывают…

Вот мы и освоили переход от величин к процентам и обратно. Можно браться за задачки.

Задачи на проценты.

В ЕГЭ задачи на проценты очень популярны. От самых простых до сложных. В этом разделе мы работаем с простыми задачами. В простых задачах, как правило, нужно перейти от процентов к тем величинам, о которых идёт речь в задаче. К рублям, килограммам, секундам, метрам, и так далее. Или наоборот. Это мы уже умеем. После этого задача становится понятной и легко решается. Не верите? Смотрите сами.
Пусть у нас есть такая задачка.

«Проезд на автобусе стоит 14 рублей. В дни школьных каникул для учащихся ввели скидку 25%. Сколько стоит проезд на автобусе в дни школьных каникул?»

Как решать? Если мы узнаем, сколько 25% в рублях – то и решать-то нечего. Отнимем скидку от исходной цены – и все дела!

Но мы уже умеем это узнавать! Сколько будет один процент от 14 рублей? Одна сотая часть. То есть 14/100 = 0,14 рубля. А таких процентов у нас 25. Вот и умножим 0,14 рубля на 25. Получим 3,5 рублей. Вот и всё. Величину скидки в рублях мы установили, остаётся узнать новую стоимость проезда:

Десять с половиной рублей. Это ответ.

Как только от процентов перешли к рублям, всё стало просто и понятно. Это общий подход к решению задач на проценты.

Понятное дело, не все задачи одинаково элементарны. Есть и посложнее. Подумаешь! Мы и их сейчас порешаем. Сложность в том, что всё наоборот. Нам даны какие-то величины, а найти надо проценты. Например, такая задача:

«Раньше Вася решал правильно две задачи на проценты из двадцати. После изучения темы на одном полезном сайте, Вася стал решать правильно 16 задач из 20. На сколько процентов поумнел Вася? За стопроцентный ум считаем 20 решённых задач.»

Раз вопрос про проценты (а не рубли, килограммы, секунды и т.д.), то и переходим к процентам. Узнаем, сколько процентов Вася решал до поумнения, сколько процентов после – и дело в шляпе!

Считаем. Две задачки из 20 – это сколько процентов? 2 меньше 20 в 10 раз, правильно? Значит, количество задачек в процентах будет в 10 раз меньше, чем 100%. То есть 100/10 = 10.

10%. Да, немного решал Вася… На ЕГЭ делать нечего. Но вот он поумнел, и решает 16 задач из 20. Считаем, сколько это будет процентов? Во сколько раз 16 меньше 20? Навскидку и не скажешь… Придётся делить.

В 5/4 раза. Ну а теперь делим 100 на 5/4:

Вот. 80% это уже солидно. А главное – не предел!

Но это ещё не ответ! Читаем задачу снова, чтобы не ошибиться на ровном месте. Да, нас спрашивают, на сколько процентов поумнел Вася? Ну, это просто. 80% — 10% = 70%. На 70%.

70% — это правильный ответ.

Как видите, в простых задачках достаточно перевести заданные величины в проценты, или заданные проценты – в величины, как всё и проясняется. Ясное дело, что в задачке вполне могут быть и дополнительные навороты. Которые, часто, к процентам отношения и не имеют вовсе. Тут, главное, внимательно условие читать и по шагам, не спеша, разворачивать задачку. Об этом мы в следующей теме поговорим.

Но есть в задачах на проценты одна серьёзная засада! Многие в неё попадают, да… Выглядит эта засада вполне невинно. Например, вот такая задачка.

«Красивая тетрадка летом стоила 40 рублей. Перед началом учебного года, продавец поднял цену на 25%. Однако, тетрадки стали покупать так плохо, что он снизил цену на 10%. Всё равно не берут! Пришлось ему снизить цену ещё на 15%. Вот тут торговля пошла! Какова была окончательная цена тетрадки?»

Ну, как? Элементарно?

Если вы стремительно и радостно дали ответ «40 рублей!», то вы попали в засаду…

Фокус в том, что проценты всегда считаются от чего-то.

Вот и считаем. На сколько рублей продавец взвинтил цену? 25% от 40 рублей — это 10 рублей. То есть, подорожавшая тетрадка стала стоить 50 рублей. Это понятно, да?

А теперь нам надо сбросить цену на 10% от 50 рублей. От 50, а не 40! 10% от 50 рублей – это 5 рублей. Следовательно, после первого удешевления тетрадь стала стоить 45 рублей.

Считаем второе удешевление. 15% от 45 рублей (от 45, а не 40, или 50!) – это 6,75 рубля. Стало быть, окончательная цена тетрадки:

45 – 6,75 = 38,25 рубля.

Как видите, засада заключается в том, что проценты считаются каждый раз от новой цены. От последней. Так бывает практически всегда. Если в задаче на последовательное повышение-понижение величины открытым текстом не сказано, от чего считать проценты, надо считать их от последнего значения. И то, правда. Продавец откуда знает, сколько раз эта тетрадка дорожала-дешевела до него и сколько она стоила в самом начале…

Кстати, теперь вы можете подумать, зачем в задачке про умного Васю написана последняя фраза? Вот эта: «За стопроцентный ум считаем 20 решённых задач»? Вроде и так всё ясно… Э-э-э… Как сказать. Если этой фразы не будет, Вася вполне может посчитать за 100% свои начальные успехи. То есть две решённые задачки. А 16 задач – в восемь раз больше. Т.е. 800% ! Вася сможет вполне оправданно говорить о собственном поумнении аж на 700%!

А ещё можно и 16 задач взять за 100%. И получить новый ответ. Тоже правильный…

Отсюда вывод: самое главное в задачах на проценты – чётко определить, от чего надо считать тот или иной процент.

Это, кстати, и в жизни надо. Там, где проценты используются. В магазинах, банках, на акциях всяких. А то ждёшь 70% скидки, а получаешь 7%. И не скидки, а удорожания… И всё честно, сам просчитался.

Ну вот, представление о процентах в математике вы получили. Отметим самое важное.

1. В задачах на проценты – переходим от процентов к конкретным величинам. Или, если надо – от конкретных величин к процентам. Внимательно читаем задачу!

2. Очень тщательно изучаем, от чего нужно считать проценты. Если об этом не сказано прямым текстом, то обязательно подразумевается. При последовательном изменении величины, проценты подразумеваются от последнего значения. Внимательно читаем задачу!

3. Закончив решать задачу, читаем её ещё раз. Вполне возможно, вы нашли промежуточный ответ, а не окончательный. Внимательно читаем задачу!

Решите несколько задач на проценты. Для закрепления, так сказать. В этих задачках я постарался собрать все главные трудности, которые поджидают решающих. Те грабли, на которые чаще всего наступают. Вот они:

1. Элементарная логика при анализе простых задачек.

2. Правильный выбор величины, от которой нужно считать проценты. Сколько народу споткнулось на этом! А ведь есть оч-ч-чень простое правило.

3. Проценты от процентов. Мелочь, а смущает здорово.

4. И ещё одни вилы. Связь процентов с дробями и частями. Перевод их друг в друга.

«В олимпиаде по математике принимали участие 50 человек. 68% учеников решили мало задач. 75% оставшихся решили средне, а остальные – много задач. Сколько человек решило много задач?»

Подсказка. Если у вас получаются дробные ученики – это неправильно. Читайте внимательно задачу, есть там одно важное слово… Ещё задачка:

«Вася (да-да, тот самый!) очень любит пончики с повидлом. Которые пекут в булочной, через одну остановку от дома. Стоят пончики по 15 рублей за штуку. Имея в наличии 43 рубля, Вася поехал в булочную на автобусе за 13 рублей. А в булочной шла акция «Скидка на всё – 30%. ». Вопрос: сколько дополнительных пончиков не смог купить Вася из-за своей лени (мог бы и пешком прогуляться, правда?)»

На сколько процентов 4 меньше 5?

На сколько процентов 5 больше 4?

Коля устраивался на несложную работу, связанную с расчётом процентов. При собеседовании начальник с хитрой улыбкой предложил Коле два варианта оплаты труда. По первому варианту Коле сразу назначалась ставка 15000 руб в месяц. По второму Коле, если он согласится, первые 2 месяца будут выплачивать пониженную на 50% зарплату. Типа, как новичку. Зато потом увеличат его пониженную зарплату аж на 80%!

Коля посещал один полезный сайт в Интернете. Поэтому, подумав шесть секунд, с лёгкой улыбкой выбрал первый вариант. Начальник улыбнулся в ответ и установил Коле постоянную зарплату в 17000 руб.

Вопрос: Сколько денег в расчёте за год (в тысячах рублей) Коля выиграл на этом собеседовании? Если сравнивать с самым неудачным вариантом? И ещё: что они всё время улыбались-то!?)

Опять короткая задачка.

И снова длинная.)

Скорый поезд №205 «Красноярск — Анапа» сделал остановку на станции «Сызрань-город». Василий и Кирилл пошли в привокзальный магазинчик за мороженым для Лены и гамбургером для себя. Когда они купили всё необходимое, уборщица магазина сообщила, что их поезд уже поехал. Василий и Кирилл быстро-быстро побежали и успели заскочить в вагон. Вопрос: успел бы в этих условиях заскочить в вагон чемпион мира по бегу?
Считаем, что в обычных условиях чемпион мира бежит на 30% быстрее Василия и Кирилла. Однако, стремление догнать вагон (он был последний), угостить Лену мороженым и съесть гамбургер, увеличило их скорость на 20%. А мороженое с гамбургером в руках чемпиона и шлёпанцы на ногах уменьшили бы его скорость на 10%.

А вот задачка без процентов. Интересно, зачем она здесь?)

Определить, сколько весит 3/4 яблока, если всё яблоко весит 200 граммов?

В скором поезде №205 «Красноярск — Анапа» попутчики разгадывали сканворд. Лена отгадала 2/5 всех слов, а Василий отгадал одну треть оставшихся. Затем подключился Кирилл и разгадал 30% всего сканворда! Серёжа отгадал последние 5 слов. Сколько всего слов было в сканворде? Верно ли, что Лена отгадала больше всех слов?

Ответы в традиционном беспорядке и без наименований единиц. Где пончики, где ученики, где рубли с процентами – это вы уж сами…

10; 50; да; 4; 20; нет; 54; 2; 25; 150.

Ну и как? Если всё сошлось — поздравляю! Проценты — не ваша проблема. Можно смело идти работать в банк.)

Что-то не так? Не получается? Не умеете быстро считать проценты от числа? Не знаете очень простых и понятных правил? От чего считать проценты, например? Или, как перевести дроби в проценты?

Тогда вам в Особый раздел 555. Там, в теме «Задачи на проценты», детально разобраны решения всех этих задач. Приведены очень простые и понятные правила работы с процентами. Тем, кто знает эти правила, проценты уже не страшны. Они им симпатичны.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

А вот здесь можно познакомиться с функциями и производными.

www.egesdam.ru

Как решать задачи на проценты в 6 классе

Предлагаю вашему вниманию легкий способ разобраться, как решать задачи на проценты в 6 классе.

При решении задачи на проценты первым делом нужно определить вид задачи. Задачи на проценты в 6 классе можно подразделить на три вида:

Определить вид задачи на проценты можно по записи ее условия. Если напротив 100% стоит число, то это — задача на нахождение процентов от числа. Если число напротив 100% неизвестно, то это — задача на нахождение числа по его процентам. Если же неизвестное значение стоит в колонке процентов, то это — задача на нахождение процентного отношения двух чисел.

Рассмотрим на примерах, как научиться определять вид задачи на проценты.

1. Из картофеля выходит 20% крахмала. Сколько крахмала выйдет из 45 т картофеля?

Это задача на нахождение процентов от числа (так как напротив 100% стоит число).

2. Руда содержит 67% железа. Сколько нужно руды для получения 13,4 т железа?

Это задача на нахождение числа по его процентам (так как напротив 100% стоит ?)

3. Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.

Это задача на процентное отношение (так как в колонке процентов стоит ?).

31 Comments

Спасибо, вы очень помогли) Хороший сайт, интересный подход к задачам…только…не было бы этих пошлых реклам =

Уважаемый (ая) ххх! Работа над сайтом требует много сил и времени. Кроме того, нужно оплачивать хостинг и доменное имя. Поэтому хорошо, когда реклама есть.

Здравствуйте ваш сайт меня спасает , ? у вас есть задачи на 8 — 9 классы ?

огромное вам спасибо мне завтра cдавать экзамены для поступления в кадетское училище и сайт очень помог я все вспомнил что мы проходили в школе

Саша, желаю Вам успешной сдачи экзаменов!

А расскажите, пожалуйста, простой способ, как можно решить подобную задачу:

Прайс повысился сначала на 7%, а потом еще на 5%. На сколько процентов выросла первоначальная цена?

Или вот еще такое:
УСН составляет 6% Как узнать, на сколько процентов нужно увеличить сумму платежа, чтобы полностью компенсировать эти 6% (если просто прибавить к сумме 6%, то и значение для 6% увеличится, а значит сумма «на руки» тоже получится чуть меньше…).

Мне скоро поступать в финский ВУЗ на бизнес-специальность. Математика была давно. А таких задач в тесте — больше половины ? Вроде, и не сложно. Но я пока не могу сообразить, что к чему.

Самый простой способ (но это на мой взгляд) — первоначальную цену можно обозначить, к примеру, а. Это 100%. После увеличения на 7% цена составила 107% от первоначальной, то есть 1,07а. После увеличения цены еще на 5% получим 1,05∙1,07а=1,1235а. Разница между новой и первоначальной ценой составляет 1,1235а-а=0,1235. Переводим десятичную дробь в проценты: 0,1235=12,35%. Здесь подробнее.
Другую задачу завтра посмотрю. Извините, засыпаю. Еще ошибусь где-либо, дети станут возмущаться: «Как вы смеете других учить, а сами ошибки делаете?» ?

Я для себя решил немного по-другому. В задачах о процентах всегда есть первоначальное число — база (Б), результат изменения (Р) и пропорция — коэффициент изменения базы (к).

Одно соотношение: Р=Б*к.

Если база Б уменьшилась на 6%, то к=0,94.

при известном результате (сумма платежа, допустим 100 единиц) — Р, базу находим так:

проверка: если от 106,383 вычесть 6%, получится 100.

Вся беда и путаница в калькуляторах в том, что знак процентов работает только с одним типом задач «нахождение результата при известной базе».
Так мне кажется.

Спасибо огромное Вам, Светлана! Дочь проболела все задачи на проценты. Чтобы ей помочь, обратилась к Вашему сайту. Все так понятно и просто! Успехов Вам и удачи во всем!

Спасибо, Ольга! Желаю здоровья и успехов Вам и дочери!

спасибо завтра а олимпиаду ехать а я забыл темы много болел отличник но забыл по болезням

Игорь, желаю Вам здоровья и отличного результата на олимпиаде!

Здравствуйте Светлана. У меня такая задача сможете помочь с ответом. Гуля весит 42 кг, а Боря 82 кг. Вот вопрос на сколько % Гуля меньше чем Боря . И на скобки % Боря тежелее чем Гуля . У этой задачи 1 ответ должен быть . Или нет .

Гуля, это две разные задачи.
1. Так как нужно найти, на сколько процентов вес Гули меньше веса Бори, то 100% здесь — вес Бори (как уровень для сравнения).
________кг_______%
Боря____82____100
Гуля____42_____х

1) Составляем пропорцию и решаем её:

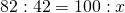
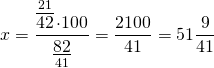
Значит, вес Гуля составляет 51 9/41 % от веса Бори.

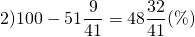
на столько процентов вес Гули меньше веса Бори.
2. Так как требуется найти, на сколько Боря тяжелее, чем Гуля, в качестве 100% здесь берём вес Гули.
________кг_______%
Гуля____42_____100
Боря____82______х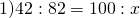

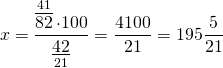
столько процентов составляет вес Бори от веса Гули.

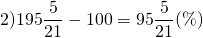
на столько процентов Боря тяжелее Гули.

Помогите пожалуйста решить задачку! Мужчина продал машину за 220000 руб, он заработал на ней 20%. за какую сумму он ее купил?

Первоначальная цена машины составляет 100%. Так как мужчина заработал на продаже 20%, то он продал её за 120% от первоначальной цены.
____________руб___________%
Купил_____х___________100
Продал___220000____120
Составляем пропорцию и решаем её: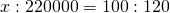

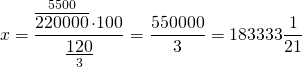
За столько рублей мужчина купил машину.

Помогите пожалуйста с задачей!У Алёши 80 марок, у Бори на 20% больше,а у Вовы на 25% меньше. Сколько марок у Вовы и у Бори в отдельности?

20% — это 1/5 часть числа. 80:5=16. Значит, у Бори на 16 марок больше, чем у Алёши, то есть у него 80+16=96 марок.
25% — это 1/4 часть числа. 80:4=20. Следовательно, у Вовы на 20 марок меньше, чем у Алёши, то есть у Вовы 80-20=60 марок.

доброе утро. Сегодня котрольная,не могу решить такую залачу, помогите пожалуйста. Сплав, который используется при паянии, составляет 58% свинца и 2,5% разных примесей. Остальной сплав — олово. Найдите массу куска этого сплава, если в нем свинца на 22,2 г больше, чем олова.

Добрый день, Алёша!
1) 100-(58+2,5)=39,5 (%) сплава составляет олово
2) 58-39,5=18,5 (%) на столько свинца больше, чем олова.
3) 22,2:18,5=1,2 (г) в 1%
4) 1,2∙100=120 (г) масса сплава.

На покраску куба размером 2×2×2 требуется 2 грамма краски сколько краски потребуется на покраску куба размером 6×6×6

В 9 раз больше. Но какое отношение Ваш вопрос имеет к решению задач на проценты в 6 классе?

Последняя задача про краску не дает мне покоя, так как у меня другой ответ. Начинаю в себе сомневаться. Пожалуйста, подтвердите мое решение или опровергните, если не трудно.
2*2*2=8
6*6*6=216
216/8=27 раз
2г*27=54г
Заранее благодарна

Речь идет о площади поверхности куба. Поверхность куба состоит из 6 граней, каждая грань — квадрат со стороной а. Соответственно, площадь поверхности куба вычисляется по формуле S=6a². Для куба с ребром a=2 S=6∙2²=24, для куба с ребром a=6 — S=6∙6²=216. Площадь поверхности увеличилась в 9 раз.

Светлана Михайловна, спасибо большое!. Меня заклинило на объемах, я поняла.Очень Вам благодарна.

Задача про веса Бори и Гули очень помогла разобраться, спасибо большое!

Здравствуйте, Светлана.Решите пожалуйста задачу. Бак автомобиля вмещает 60 л бензина. Сколько литров бензина в баке, если заполнено 55% его объема?

Это задача на нахождение процентов от числа.
1) 55%=0,55
2) 0,55∙60=33(л) бензина в баке.

ПОМОГИТЕ РЕШИТЬ!!
В первый день посадили лес на 38% всей площади,во второй день на 32.8 %,а в третий на оставшихся 7.3га.Чему равна площадь отведенная под посадку леса?

Весь лес — 100%. На третий день посадили 100- (38+32,8)=29,2%. Проще всего решить задачу с помощью пропорции. Примем площадь леса за х:
х:100=7,3:29,2. Отсюда х=7,3∙100:29,2 и х=25.
Если пропорцию ещё не изучали — тогда нахождение числа по его процентам: 1)29,2%=0,292; 2) 7,3:0,292=35 (га).

www.for6cl.uznateshe.ru