Правила суммы и произведения в комбинаторике

Большинство комбинаторных задач решается с помощью двух основных правил — правила суммы и правила произведения.

Правило суммы. Если некоторый объект 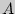можно выбрать 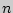способами, а другой объект 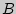можно выбрать 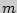способами, то выбор «либо 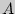, либо 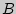» можно осуществить 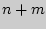способами.

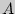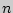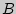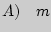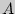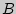Правило произведения. Если объект можно выбрать способами, а после каждого такого выбора другой объект можно выбрать (независимо от выбора объекта способами, то пары объектов и можно выбрать способами.

Пусть 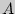= <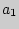, , 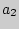. 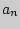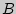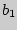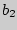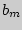>, = <, , . > и А — число элементов множества 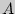. Составим декартово произведение 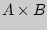множеств 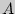и 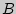, т.е. множество пар (, .

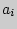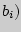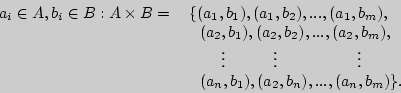
Тогда правило произведения записывается следующим образом:

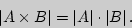
Пример 6. Сколько существует двузначных чисел?

Решение. Поскольку в двузначном числе цифра, обозначающая число десятков, должна быть отлична от нуля, то 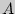= <1, 2, . 9>, 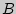= <0, 1, 2, . 9>и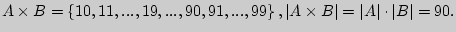

Размещениями из 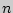элементов по 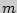называются такие выборки, которые, имея по 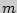элементов, выбранных из числа данных 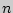элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Число размещений из 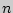элементов по 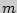обозначим 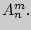Используя основное правило комбинаторики, получаем

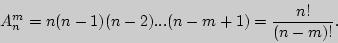
Если , то 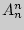— число таких размещений, которые отличаются только порядком расположения элементов. Такие размещения называются перестановками. Их число 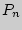находится по формуле

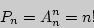
Выборки из 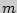элементов, взятых из данных 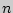, отличающихся только составом элементов, называются сочетаниями из 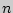элементов по 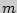. Число 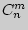таких сочетаний находится

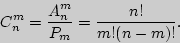
Пример 7. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, немецкого, французского, испанского — на любой другой из этих пяти языков?

Решение. Поскольку важен порядок, с какого языка задается перевод на другой, то для ответа на вопрос необходимо найти число размещений из пяти по два.

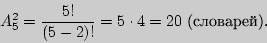
Пример 8. В соревнованиях на первенство университета по волейболу участвуют 8 команд. Насколько более продолжительным будет турнир, организованный по круговой системе, чем по олимпийской?

Решение. При проведении турнира по круговой системе каждый участник встречался с каждым и порядок их вхождения в пару не важен. Следовательно, по круговой системе потребуется провести 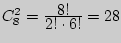встреч, а по олимпийской только — 7 (четыре встречи в 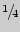финала, две — в полуфинале и одна в финале).

В данных выборках допускается повторение элементов, что является достаточно естественным (например, в телефонных и автомобильных номерах возможно использование одной цифры несколько раз).

Число размещений из 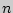элементов по 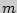с повторениями обозначается 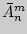и находится как

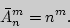
Число перестановок 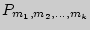, в которых 1-й элемент повторяется 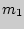раз, 2-й — 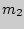раз, а 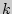-й — 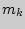раз, находится следующим образом:

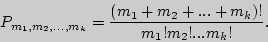
Пример 9. Сколько «слов» можно получить, переставляя буквы в слове МАТЕМАТИКА?

Решение. Заметим, что если бы все буквы были различны, то получили бы 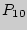новых «слов», но буква «М» употребляется в «слове» 2 раза, «А» — 3 раза, «Т» — 2 раза, оставшиеся три буквы — по разу. Следовательно, искомое число будет в 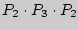раз меньше, чем 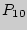, и равно

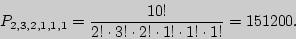
Число сочетаний с повторениями 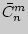из 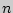элементов по 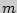выражается через число сочетаний без повторений:

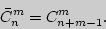
Пример 10. В кафе в продаже имеются 5 сортов пирожных. Сколькими способами 8 студенток могут заказать себе по одному пирожному?

Решение. Зашифруем каждую покупку 8 пирожных единицами по 5 сортам, разделяя сорта нулями. Тогда каждой покупке будет соответствовать упорядоченный набор из 8 единиц и 4 (= 5 — 1) разделительных нулей, а общее число покупок будет соответствовать числу перестановок этих нулей и единиц 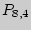. Таким образом,

Вопросы для самоконтроля

1. Основные правила комбинаторики и их иллюстрация на графе.
2. Порядок решения комбинаторных задач.
3. Приведите примеры размещений и перестановок без повторений.
4. Свойства сочетаний без повторений.
5. Как получить треугольник Паскаля, и где он применяется?
6. Приведите примеры выборок с повторениями.
7. Каких выборок больше: с повторениями или без повторений?
8. Что понимают под словом длины 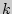над алфавитом ?

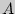I 11. В чемпионате России по футболу участвуют 16 команд. Сколькими способами может определиться тройка призеров?

12. Из колоды, содержащей 36 карт, вынули 10 карт. Сколькими различными способами это можно сделать? В скольких случаях среди этих карт окажется хотя бы один туз? В скольких случаях окажется ровно один туз?

13. Сколькими способами 8 человек могут встать в очередь друг за другом?

14. Сколькими способами можно расставить на книжной полке 5 учебников по комбинаторике, 4 — по алгебре и 3 — по математическому анализу, если учебники по каждому предмету одинаковые?

15. На физмате работают 76 преподавателей. Из них 49 знают английский язык, 32 — немецкий и 15 — оба языка. Сколько преподавателей на физмате не знает ни английского, ни немецкого языков?

16. В цветочном магазине продаются цветы 4 сортов. Сколько можно составить различных букетов из пяти цветов в каждом?

II 17. В азбуке Морзе буквы представляются последовательностями тире и точек. Сколько символов потребуется, чтобы закодировать буквы русского алфавита?

18. Какова вероятность выиграть хотя бы один из призов в спортлото?

III 19. Доказать с помощью комбинаторных рассуждений тождество

cito-web.yspu.org

Как решать задачи по комбинаторике?

Комбинаторная теория является одной из важнейших областей математики, без знания которой не обойтись ни менеджеру, ни программисту, ни другим специалистам. Знать, как проводится решение задач по комбинаторике, значит быть востребованным работником, умеющим решать широкий круг практических задач.

Возникновение комбинаторной теории

Комбинаторика – это область математики, изучающая вопрос, сколько разных комбинаций (наборов) можно составить из элементов заданного множества. При этом нужные комбинации подчиняются определенным требованиям, что приводит к различным методам решения задач по комбинаторике.

Истоки этой науки были положены знаменитым математиком и философом Готфридом Лейбницем.

Два основных правила комбинаторной теории

Теория комбинаторики зиждется на двух основных принципах – это правило сложения и правило умножения. Рассмотрим их подробнее.

Правило сложения: Пусть объект А мы можем выбрать из множества $m$ способами, а объект В можно выбрать $n$ способами, то объект «А+В» можно выбрать $m+n$ способами.

Возможно, это правило покажется непосвященному человеку абракадаброй, но ничего сложного нет. Рассмотрим пример – пусть в одном ящике есть $m$ шариков, а во втором ящике – $n$ шариков. Сколькими способами можно вытащить шарик из одного этих ящиков. Очевидно, что ОДИН шарик можно достать $m+n$ способами.

Правило умножения: Пусть объект А выбирается $m$ способами, объект В выбирается $n$ способами, то оба объекта можно выбрать $mn$ способами.
Все очень просто – каждый из $m$ способов выбора объекта А комбинируется с каждым из $n$ способов выбора объекта В, то есть количество способов просто умножается друг на друга.

Рассмотрим простой пример: сколько чисел можно составить из цифр 0,1,2,3,4,5,6,7,8,9, если число должно быть двузначным?
Можно составить 90 чисел – первую цифру числа (объект А) можем выбрать 9 способами, так как число не может начинаться с нуля. Вторую цифру числа (объект В) можем выбрать 10 способами, так как у нас есть 10 цифр. Итого получается $9*10=90$ чисел.

Это были главные правила, на которые опираются все методы решения задач по комбинаторике. Еще больше теории о началах комбинаторики вы найдете в онлайн учебнике: Элементы комбинаторики онлайн.

Готовые решения задач по теории вероятностей, в том числе по комбинаторике — более 400 решений. Найди свою задачу:

Примеры решения задач по комбинаторике

Перейдем к более продвинутым случаям и рассмотрим другие понятия комбинаторики.

Есть 5 книг. Сколькими способами их можно расположить на книжной полке?
Ответ – 120 способов. Первую книгу можем выбрать 5 способами, вторую книгу 4 способами и т.д. Перемножая числа с 5 до 1, получим 120.

С этой задачи начинается понятие факториала. N-факториал или N! – это количество перестановок из N объектов, вычисляемое по формуле $P_N =N!= 1*2*3*…*(N-1)*N$.

Следующий пример – в чемпионате мира участвуют 18 команд по футболу. Сколькими способами можно распределить золотые, серебряные и бронзовые комплекты?
Ясно, что золотые медали может получить любая из команд, значит золотого призера (объект А) можно выбрать 18 способами. Остается два комплекта и 17 команд. Серебряным медалистом может стать одна из 17 команд, а бронзовым – одна из 16 команд. Значит, серебряного и бронзового медалиста можно выбрать 17 и 16 способами.
Итого, три комплекта медалей могут распределиться 18*17*16 = 4896 способами.

www.matburo.ru

2. Правила суммы и произведения

В комбинаторике, которая возникла раньше теории множеств, правило нахождения числа элементов объединения двух непересекающихся конечных множеств называют правилом суммы и формулируют в таком виде:

Если объект а можно выбрать т способами, а объект b – k способами (не такими, как а), то выбор «либо а, либо в» можно осуществить т + k способами.

Задача 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?

Решение. По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу суммы, можно осуществить 5 + 4 = 9 способами.

Правило нахождения числа элементов декартова произведения двух множеств называют в комбинаторике правилом произведения и формулируют в таком виде:

Если объект а можно выбрать т способами, а объект b – k способами, то пару (а, b) можно выбрать m  k способами.

Замечание. Правило суммы и произведения, сформулированные для двух объектов можно обобщить и на случай t.

Задача 2. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из яблока и апельсина?

Решение. По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе пары (яблоко, апельсин), то ее, согласно правилу произведения, можно выбрать 5  4 = 20 способами.

Задача 3. Сколько всего двузначных чисел можно составить из цифр 7, 4 и 5 при условии, что они в записи числа не повторяются?

Решение. Чтобы записать двузначное число, надо выбрать цифру десятков и цифру единиц. Согласно условию на месте десятков в записи числа может быть любая из цифр 7, 4 и 5. Другими словами, выбрать цифру десятков можно тремя способами. После того, как цифра десятков определена для выбора цифры единиц остаются две возможности, поскольку цифры в записи числа не должны повторятся. Так как любое двузначное число – это упорядоченная пара, состоящая из цифры десятков и цифры единиц, то ее выбор, согласно правилу произведения, можно осуществить 3  2 = 6 способами.

Задача 4. Сколько трехзначных чисел можно составить, используя цифры 7, 4 и 5?

Решение. В данной задаче рассматриваются трехзначные числа, так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбирать тремя способами каждую. Поскольку запись трехзначного числа представляет собой каждую. Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 27 способами, так как 3  3  3 = 27.

Задача 5. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?

Решение. Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру – цифру тысяч можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо нуль, либо три, т.е. два способа выбора. Сколько же способов выбора имеется для цифры десятков и цифры единиц.

Итак, цифру тысяч можно выбрать одним способом, цифру сотен – двумя, цифру единиц двумя. Чтобы узнать сколько всего четырехзначных чисел можно составить из цифр 0 и 3, согласно правилу произведения, способы выбора каждой цифры надо перемножить: 1 2  2  2 = 8.

Таким образом, имеем 8 четырехзначных чисел.

Задача 6. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?

Решение. Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить также пятью способами, поскольку цифры в записи числа не должны повторятся, а одна из шести данных цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что всего трехзначных чисел (из данных шести цифр) можно образовать 100: 5  5  4 = 100.

studfiles.net

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

.

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

ya-znau.ru

Комбинаторика. Правила суммы и произведения. Решение задач

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Напоминаем, что в соответствии с профстандартом педагога (утверждён Приказом Минтруда России), если у Вас нет соответствующего преподаваемому предмету образования, то Вам необходимо пройти профессиональную переподготовку по профилю педагогической деятельности. Сделать это Вы можете дистанционно на сайте проекта «Инфоурок» и получить диплом с присвоением квалификации уже через 2 месяца!

Только сейчас действует СКИДКА 50% для всех педагогов на все 111 курсов профессиональной переподготовки! Доступна рассрочка с первым взносом всего 10%, при этом цена курса не увеличивается из-за использования рассрочки!

Непосредственное применение комбинаторных правил произведения (умножения) и суммы.

1) Правило суммы. Если объект Х можно выбрать n способами, а объект Y можно выбрать m способами, причём эти способы выбора несовместны, то объект « Х или Y » можно выбрать n + m способами.

Несовместность способов выбора означает, что ни один способ выбора объекта Х не совпадает ни с одним способом выбора объекта Y .

Пример 1. Сколькими разными способами можно заказать напиток в кафе, где есть 8 видов сока и 5 видов минеральной воды?

Решение. Напиток – это или сок (объект Х ), или минеральная вода (объект Y ). Сок можно выбрать 8-ю разными способами, минеральную воду – 5-ю, причем способы выбора несовместны. Тогда по правилу суммы напиток (объект « Х или Y ») можно выбрать 8+5=13-ю способами.

Пример 2. Пусть есть колода карт (36 листов). Объект Х – карта червовой масти – может быть выбран 9-ю разными способами. Объект Y – туз – может быть выбран 4-мя разными способами. Сколькими способами может быть выбран объект « Х или Y » – «червовая карта или туз»?

Решение. В этом примере правило суммы не работает , так как способы выбора объектов X и Y совместны: один из способов выбора объекта X совпадает с одним из способов выбора объекта Y (выбор червового туза – это и способ выбора объекта X , и способ выбора объекта Y ).

Задача решается перебором подходящих карт: червовых карт 9 и ещё 3 туза (один уже учтён). Значит, червовую карту или туз можно выбрать 9+3=12-ю способами.

Пример показывает, что при использовании правила суммы необходимо проверять несовместность выборов. В противном случае, можно получить неверный ответ.

На практике интуиция учащихся обычно работает так, что при решении задачи рассматриваются несовместные выборы. Поэтому постоянная проверка условия несовместности «надоедает» и её перестают осуществлять. А это может привести к тому, что «в один прекрасный момент» правило суммы ошибочно будет применено там, где оно не работает! Можно посоветовать учащимся при получении явно неверного ответа вспомнить, что ошибка могла быть именно в этом!

Правило суммы может быть применено к любому конечному числу объектов.

Пример 3. На книжной полке стоит 3 учебника по математике, 4 детектива, 2 задачника по теории вероятностей, 3 любовных романа, 2 сборника стихов и справочник по математике. Сколькими разными способами можно выбрать почитать художественную книгу?

Решение. Художественная книга – это или детектив (объект X ), или роман (объект Y ), или сборник стихов (объект Z ). Детектив можно выбрать 4-мя разными способами, роман – тремя, сборник стихов – двумя. Способы выбора несовместны, так как книг смешанного жанра нет. Тогда, применяя правило суммы к трём объектам, получаем, что художественную книгу, то есть объект « X или Y , или Z », можно выбрать 4+3+2=9-ю способами.

2) Правило произведения. Пусть объект Х может быть выбран n способами и после каждого такого выбора объект Y может быть выбран m способами. Тогда пара « Х и Y » может быть выбрана способами.

Пример. В гардеробе имеется 3 юбки (чёрная, коричневая, фиолетовая) и 4 блузки (белая, сиреневая, желтая и розовая). Сколько разных нарядов можно из них составить?

Решение. Эту задачу можно решать перед формулировкой правила произведения. При этом целесообразно использовать граф для перебора всех вариантов:

Юбку можно выбрать тремя разными способами. Для каждого из них блузку можно выбрать 4-мя способами. Тогда по правилу произведения весь наряд, то есть юбку и блузку, можно выбрать 3 -ю способами.

Правило произведения справедливо для выбора любого конечного числа объектов.

Правило произведения в общем виде. Пусть элемент может быть выбран числом способов. Для каждого способа выбора следующий элемент может быть выбран числом способов. Для каждого способа выбора двух элементов , третий элемент может быть выбран числом способов и т.д. Наконец, для каждого способа выбора элементов элемент может быть выбран числом способов. Тогда кортеж может быть выбран числом способов.

Пример. Сколько существует различных четырёхзначных чисел, составленных из чётных цифр так, что все цифры в числе различны?

Решение. Чётные цифры: 0, 2, 4, 6, 8. Четырёхзначное число – это число, состоящее из четырёх цифр, причем первая цифра не равна нулю. То есть это кортеж . Начинаем составлять число с требуемыми свойствами. Первую цифру можно выбрать 4-мя способами (любую чётную цифру, кроме нуля). Для любого из 4-х способов выбора первой цифры вторую цифру можно выбрать тоже 4-мя способами (любую чётную, кроме той, которая уже выбрана на первое место). После этого третью цифру можно выбрать 3-мя способами. А для любого способа выбора первых трёх цифр четвёртую всегда можно выбрать 2-мя способами. Тогда по правилу произведения все четыре цифры, то есть нужное число, можно выбрать 4 способами. Следовательно, существует 96 различных четырёхзначных чисел, в которых все цифры не повторяются.

Замечание. Необходимо обратить внимание учащихся на равносильность вопросов:

«Сколько существует четырёхзначных чисел, в которых все цифры различны?»

«Сколькими способами можно выбрать четырёхзначное число, в котором все цифры различны?»

«Сколько можно составить четырёхзначных чисел так, чтобы цифры в числе не повторялись?»

Договориться с учениками о способе оформления задач на правило произведения (ступенька!)

1 . Ф. Сколько различных трехзначных чисел, в записи которых цифры могут повторяться, можно записать с помощью цифр: 1)1, 2, 3,4; 2)0,1,2,3?

1) Составляем трехзначные числа из цифр 1, 2, 3, 4 с повторениями: первую цифру можно выбрать 4 способами, вторую и третью -тоже 4 способами, всего можно составить 4-4-4 = 4 =64 различных трехзначных чисел.

2) Составляем трехзначные числа из цифр 0, 1, 2, 3 с повторениями: первую цифру можно выбрать 3 способами (ноль нельзя), вторую и третью — 4 способами каждую; всего можно составить 3 • 4 • 4 = 48 различных трехзначных чисел.

Ответ: 1) 64; 2) 48.

2 . Ф. Сколько различных трехзначных чисел можно записать с помощью цифр 6, 7, 8, 9, 0 при условии, что цифры в числе: 1) могут повторяться; 2) должны быть различными?

1) Составляем трехзначные числа из пяти цифр 6, 7, 8, 9, 0 с повторениями:

первую цифру выбираем 4 способами (ноль нельзя); вторую и третью цифры — 5 способами каждую, всего можно составить 4 • 5 • 5 = 100 различных трехзначных чисел.

2) Составляем трехзначные числа из пяти цифр 6, 7, 8, 9, 0 без
повторений: первую цифру можно составить 4 способами (ноль нельзя),

М-задачи из уч. пособия А.Г.Мордковича

Т- под ред. С.А.Теляковского

вторую — тоже 4 способами (из пяти данных цифр, включая ноль, но исключая цифру, выбранную на первую позицию), третью цифру — 3 способами, всего можно составить: 4 • 4 3 = 48 различных трехзначных чисел.

Ответ: 1) 100; 2)48.

3. Т. Сколько существует четырехзначных чисел, кратных 10, если цифры в числах могут повторяться?

Четырехзначное число кратно 10, если его первая цифра не ноль, а последняя — только ноль. Задачу проще всего решить прямым применением правила произведения: первую цифру можно выбрать 9 способами, вторую — 10, третью -10 (выбор с повторением), четвертую — 1. По правилу произведения количество чисел равно: = 900.

Ответ: 900 чисел.

4. Т. Из цифр 1, 2, 3, 5 составили все возможные четырехзначные числа (без повторения цифр). Сколько среди них таких чисел, которые больше 2000, но меньше 5000?

Четырехзначные числа, большие 2000, но меньшие 5000, начинаются с цифр 2 или 3 (из данных 4 цифр). Задачу проще всего решить прямым применением правила произведения: выбор первой цифры — 2 способа, второй — 3 способа, третьей -2 способа, четвертой — 1; по правилу произведения количество чисел равно чисел.

5. Т. Из села Дятлова в село Матвеевское ведут три дороги, а из села Матвеевское в село Першино — четыре дороги. Сколькими способами можно попасть из Дятлова в Першино через Матвеевское?

Для проезда из Дятлова в Матвеевское можно выбрать одну из трех дорог; после этого для проезда из Матвеевского в Першино можно выбрать одну из четырех дорог. Каждый вариант первого выбора может сочетаться с каждым вариантом второго выбора, потому по правилу произведения общее количество вариантов равно: = 12.

Замечание. В задаче 2 выбора, но каждый выбор осуществляется из своего множества вариантов; выбираемые пары являются упорядоченными (сначала — путь из Д в М, затем — путь из М в П).

6.Т. В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?

По условию задачи последовательно осуществляются три выбора, но каждый выбор — из своего множества вариантов; поэтому выборы независимы, а каждая выбираемая тройка блюд оказывается упорядоченной (первое — второе — третье). По правилу произведения общее число способов выбрать обед равно

Ответ: 30 способов.

7.Ф. Имеется 6 видов овощей. Решено приготовить салат из 3 видов. Сколько различных (по сочетанию видов овощей) вариантов салатов можно приготовить?

Если считать, что порядок выбора овощей для салата важен и должен учитываться (что кажется странным), то можно приготовить: 6 • 5 • 4 = 120 вариантов салата. Если порядок выбора значения не имеет, то это число нужно разделить на количество различных перестановок из трех элементов, равное = 3! = 6; тогда получим =20 различных вариантов салатов.

Ответ: 120 или 20.

8. Ф. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций из юбок и кофт имеется у Светланы?

Юбку можно выбрать 3 способами, после этого кофту — 5 способами; всего = 15 различных комбинаций

Ответ: 15 комбинаций.

9. Т. Петр решил пойти на новогодний карнавал в костюме мушкетера. В ателье проката ему предложили на выбор различные по фасону и цвету предметы: пять пар брюк, шесть камзолов, три шляпы, две пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?

В задаче 4 последовательных выбора, каждый из своего множества вариантов. Общее количество различных карнавальных костюмов по правилу произведения равно: =180.

Ответ: 180 различных костюмов.

10. Ф. На стол бросают два игральных тетраэдра (серый и белый), на гранях каждого из которых точками обозначены числа от 1 до 4. Сколько различных пар чисел может появиться на гранях этих тетраэдров, соприкасающихся с поверхностью стола?

Первый тетраэдр может лечь на стол одной из 4 своих граней; второй тетраэдр — также одной из 4 своих граней; всего = 16 Различных пар граней (чисел).

Ответ: 16 пар чисел.

11. Ф. Мама решила сварить компот из фруктов двух видов. Сколько различных (по сочетанию видов фруктов) вариантов компотов может сварить мама, если у нее имеется 7 видов фруктов?

Начиная варить компот, мама может выбрать первым один из 7 видов фруктов, а вторым — один из 6 оставшихся; по правилу произведения получаем = 42 варианта выбора. Однако эти 42 варианта учитывают каждую пару выбранных фруктов дважды, с учетом порядка выбора (т. е. считается яблоки-груши и груши — яблоки). Однако при приготовлении компота разные фрукты закладываются в кастрюлю, как правило, одновременно. И в условии задачи говорится о вариантах по сочетанию видов фруктов, а сочетания порядок не учитывают. Поэтому полученное количество вариантов нужно разделить на 2, чтобы не учитывать порядок выбора. Получаем = 21 вариант.

Ответ: 21 вариант.

12. М. Игральный кубик бросили дважды и записали выпавшие очки. Найдите число всех возможных результатов.

Результатом двух последовательных бросаний является пара чисел — исходов (выпавшие очки при первом и при втором бросаниях). Первое бросание кубика может закончиться одним из 6 исходов, после этого второе бросание также может закончиться одним из 6 исходов. Каждый исход первого бросания может сочетаться с каждым исходом второго, поэтому общее число возможных пар исходов по правилу произведения равно = 36. Это и есть число всех возможных результатов двух бросаний кубика.

Ответ: 36 результатов.

13. Ф. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 0, 1,2, 3, 4, 5, если цифры в числе: 1) могут повторяться; 2) должны быть различными?

В этом случае на первую позицию нельзя выбрать ноль.

1)Если цифры могут повторяться, то выбор первой цифры возможен 5 способами (без нуля), а выбор второй цифры — 6 способами (любую из данных 6 цифр, считая и ноль, и цифру, выбранную первой). Всего возможно составить = 30 различных двузначных чисел.

2)Если цифры не могут повторяться, то выбор первой цифры возможен 5 способами (без нуля), а выбор второй цифры – также 5 способами (считая и ноль, но исключая ненулевую цифру, выбранную первой). Всего возможно составить = 25 чисел.

Ответ: 1) 30; 2) 25.

14. М. а) Сколько двузначных чисел можно составить из цифр 1,3,5,7,9?

б) Сколько среди них чисел, кратных 11?

в) Сколько среди них чисел, кратных 3?

а) Цифру на первую позицию в составленном числе мы можем выбрать 5 разными способами; после этого на вторую позицию цифру можно выбрать также 5 способами (предполагается, что цифры могут повторяться); всего по правилу произведения есть = 25 разных способов выбора и соответственно 25 разных двузначных чисел.

б) Двузначное число кратно 11, если обе его цифры равны, поэтому для составления такого числа достаточно сделать один выбор и выбранную цифру записать на обоих позициях. Одну цифру из 5 данных можно выбрать пятью разными способами, поэтому получаем 5 разных двузначных чисел, кратных 11.

в) Число кратно 3, если сумма его цифр делится на 3. Чтобы подсчитать количество таких чисел, нужно узнать, сколько среди всевозможных пар, отличающихся составом, но не учитывающих порядка расположения цифр в паре, можно составить из 5 данных цифр, а затем подсчитать, сколько среди этих пар таких, сумма цифр которых делится на 3 (фактически мы используем при этом метод полного перебора).

Составим все возможные пары цифр из 1,3, 5, 7, 9 (без учета порядка):

Таких пар 15. Среди них 5 пар (1-5, 3-3, 3-9, 5-7 и 9-9), сумма цифр которых делится на 3, причем три пары (1-5, 3-9 и 5-7) допускают перестановку, т. е. могут образовать по два разных числа. Таким образом, из данных 5 цифр можно составить 5 + 3 = 8 различных двузначных чисел, кратных 3.

Ответ: а) 25; б) 5; в) 5; г) 8.

15. М. Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.

а) Сколько всего стран могут использовать такую символику?

б) Сколько всего стран могут использовать такую символику с верхней белой полосой?

в) Сколько всего стран могут использовать такую символику с нижней зеленой полосой?

г) Сколько всего стран могут использовать такую символику с синей и красной полосами, расположенными рядом?

Прежде всего отметим, что в условии задачи противоречие: сначала говорят о вертикальных полосах, а потом – о верхней и нижней. Будем считать , что флаг состоит из четырех горизонтальных полос( это несущественно).

а) Нужно определить, сколько есть разных способов переставить местами 4 полосы разного цвета.

Цвет верхней полосы можно выбрать одним из 4 способов, цвет второй полосы — одним из 3 оставшихся, цвет третьей полосы -одним из 2 оставшихся, а цвет четвертой полосы — 1 способом (без выбора); по правилу произведения всего есть = 24 разных способа расположения полос на флаге, т. е. 24 разных флага.

б) Если фиксировать цвет верхней полосы, то цвета следующих полос можно выбрать =6 разными способами; получаем 6 флагов с белой верхней полосой.

в) Если фиксировать цвет нижней полосы, то цвета трех расположенных над ней полос можно выбрать =6 разными способами; получаем 6 флагов с нижней зеленой полосой.

г) Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно будет составить =6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная или красная, а под ней синяя. Каждую из этих двух двойных полос можно переставлять с оставшимися белой и зеленой полосами, получая по =6 вариантов флага. Поэтому общее количество вариантов по комбинаторному правилу суммы равно 6 + 6=12.

Ответ: а) 24; 6)6; в) 6; г) 12.

Замечание. Можно использовать в рассуждениях и правило произведения: каждый из 2 вариантов «склеивания» полос может сочетаться с 6 вариантами перестановок полос; всего 2 • 6 = 12 вариантов флага.

16.Ф. Сколько существует способов занять 1-е, 2-е и 3-е места на чемпионате по футболу, в котором участвуют: 1) 10 команд; 2) 11 команд?

На первое место можно поставить любую из 10 команд, на второе- любую из 9 оставшихся, на третье- любую из 8 оставшихся; по правилу произведения общее число способов равно

Рассуждая аналогично, получаем различных способов.

Ответ: 1) 720; 2) 990.

17.М. В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты.

а) Сколько команд участвовали в турнире?

б) Сколько команд играли в зеленых футболках?

в) У скольких команд футболки и трусы были разного цвета?

г) У скольких команд футболки и трусы были разного цвета, причем трусы были не красные?

а) Количество команд равно количеству способов выбора двух цветов из 5 данных с учетом порядка (один цвет — для футболки, другой — для трусов). В условии говорится о «всех возможных вариантах», т. е. допускается, что футболка и трусы могут быть одинакового цвета. Поэтому цвет футболки можно выбрать 5 способами, цвет трусов — также 5 способами, всего возможно 5 • 5 = 25 вариантов формы, т. е. в турнире участвовали 25 команд.

б) Если цвет футболки фиксирован, то цвет трусов можно выбрать одним из 5 способов; следовательно, в зеленых футболках играло 5 команд.

в) Если футболки и трусы должны быть разного цвета, то цвет футболки можно выбрать 5 способами, а после этого цвет трусов — только 4 оставшимися; общее число способов выбора равно 5 • 4 = 20, т. е. у 20 команд футболки и трусы разного цвета.

г) Рассмотрим два взаимоисключающих случая:

для футболки выбран не красный цвет;

для футболки выбран красный цвет.

В первом случае есть 4 способа выбрать цвет футболки, а после этого — 3 способа выбрать цвет трусов (кроме красного и цвета Футболки), всего 12 способов.

Во втором случае цвет футболки фиксирован (красный, а цвет трусов можно выбрать 4 способами (кроме красного); всего есть 4 способа выбора формы.

По комбинаторному правилу суммы общее число способов выбора формы в этом случае равно 12 + 4 = 16 способов, т. е. у 16 команд футболки и трусы разного цвета, причем трусы — не красные.

Ответ: а) 25; б) 5; в) 20; г) 16 команд.

18.Ф. Завуч составляет расписание уроков. В пятницу в 7 А классе должно быть 5 уроков, причем обязательно один сдвоенный урок — алгебра. Сколько различных вариантов расписания уроков может составить завуч на пятницу, если 3 оставшихся урока он комбинирует из литературы, истории и физики?

Будем рассматривать сдвоенный урок как один урок, тогда всего нужно поставить в расписание 4 урока. Первый урок можно выбрать из 4 вариантов, второй — из 3, третий — из 2 вариантов, а четвертым поставить оставшийся урок (возможно, это будет сдвоенный урок алгебры). Общее число вариантов расписания равно = 24.

Ответ: 24 варианта.

19.М. В контрольной работе будет пять задач — по одной из каждой пройденной темы. Задачи будут взяты из общего списка по 10 задач в каждой теме, а всего было пройдено 5 тем. При подготовке к контрольной Вова решил только по 8 задач в каждой теме. Найдите:

а) общее число всех возможных вариантов контрольной работы;

б) число тех вариантов, в которых Вова умеет решать все пять задач;

в) число тех вариантов, в которых Вова не сможет решить ни одной задачи;

г) число тех вариантов, в которых Вова умеет решать все задачи, кроме первой.

а) Первая задача может быть выбрана 10 способами, вторая тоже 10 (из задач другой темы), третья, четвертая и пятая задачи также могут быть выбраны 10 способами каждая; по правилу произведения общее число всех возможных вариантов контрольной работы равно = 105 = 100000.

б) Число вариантов, в которых Вова умеет решать все пять задач, равно = 85 = 32768.

в) Число вариантов, в которых Вова не сможет решить ни одной задачи, равно = 25 = 32.

г) Число тех вариантов, в которых Вова умеет решать все задачи, кроме первой, равно = 2-84 = 8192.

Ответ: а) 100000; б) 32768; в) 32; г) 8192.

20. Ф. При игре в крестики-нолики на поле размером клетки неопытный первый игрок делает 1-й ход: ставит крестик в любую из клеток; вторым ходом второй неопытный игрок ста вит нолик в любую из оставшихся свободных клеток, затем третьим ходом первый игрок ставит крестик и т. д. Сколько существует вариантов заполнения клеток после: 1) двух ходов; 2) трех ходов; 3) четырех ходов?

Первая клетка для заполнения может быть выбрана из 9 свободных клеток, вторая — из 8 оставшихся, и т. д.

После 2 ходов могут быть заполнены любые две клетки из = 72 возможных вариантов их выбора.

После 3 ходов могут быть заполнены любые три клетки из = 504 возможных вариантов их выбора. После 4 ходов могут быть заполнены любые 4 клетки из = 3024 возможных вариантов их выбора.

Ответ: 1) 72; 2) 504; 3) 3024.

21. М. Три вершины правильного 10-угольника покрасили в рыжий цвет, а остальные — в черный. Сколько можно провести отрезков с разноцветными концами?

Первую рыжую вершину можно соединить отрезком с любой из 10 — 3 = 7 черных вершин, после этого вторую рыжую вершину можно соединить отрезком с любой из 6 оставшихся черных вершин, а третью рыжую — с любой из 5 оставшихся черных вершин. Общее число вариантов (отрезков с разноцветными концами) по комбинаторному правилу произведения равно: = 210.

Ответ: 210 отрезков.

22.Ф. Сколькими различными способами можно назначить двух ребят на дежурство по столовой, если в классе: 1) 24 учащихся; 2) 25 учащихся?

Назначая двух дежурных по столовой, мы не учитываем порядок выбора пары из учащихся данного класса.

1) Если в классе 24 учащихся, то первого дежурного можно выбрать из 24 человек, а второго — из 23 человек. Составленные так пары учитывают порядок выбора: могут быть выбраны Иванов, затем Петров, или Петров, затем Иванов. Поэтому двух дежурных можно выбрать одним из способов.

2)Если в классе 25 учащихся, то, рассуждая аналогично, находим число способов назначения дежурных: =300 способов.

Ответ: 1) 276 способов: 2) 300 способов.

23. Ф. Имеется 7 книг, причем две из них одинаковые, а остальные книги отличаются от этих двух и различны между собой. Сколькими способами можно расставить эти книги на книжки полке при условии, что одинаковые книги в любой последовательности должны стоять рядом?

Поскольку две «склеенные» книги одинаковые, неразличимые то мы не рассматриваем перестановки их между собой.

Ответ: 720 способов.

24. Т. Учащиеся 9 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 24 учащихся?

Возможны две модели:

а) считаем, что в каждой паре только один (первый) учащийся передает свою фотографию, а второй только принимает, ничего не отдавая. Тогда порядок выбора имеет значение: есть 24 способа выбрать отдающего и 23 способа выбрать принимающего, всего 24 = 552 пары, в каждой из которых передается фотография.

б) Считаем, что в каждой паре происходит передача одновременно двух фотографий, т. е. учащиеся в паре равноправны, неразличимы. Тогда при образовании пар порядок выбора не имеет значения; количество таких пар равно =276. Количество фотографий будет в 2 раза больше, чем пар, т. е. = 552.

Можно рассуждать и проще: в классе 24 ученика, каждый должен отдать 23 своих фотографии; общее количество фотографий есть 24 • 23 = 522 (это наша первая модель).

Ответ: 522 фотографии.

25. Ф. Вася забыл вторую и последнюю цифры пятизначного номера телефона приятеля. Какое наибольшее число звонков предстоит сделать Васе, если он решил перепробовать комбинации всех забытых цифр, чтобы в результате дозвониться до приятеля?

Васе предстоит проверить 10 вариантов выбора второй цифры и 10 вариантов выбора пятой цифры телефонного номера; остальные цифры, известные Васе, на перебор никак не влияют. По правилу произведения наибольшее число вариантов номеров, которые предстоит проверить Васе, равно = 100 вариантов.

Ответ: максимум 100 вариантов.

Афанасьев В.В. Теория вероятностей в примерах и задачах, — Ярославль: ЯГПУ , 1994.

Баврин И. И. Высшая математика: Учебник для студентов химико-математических специальностей педагогических вузов-2-е издание, переработанное. — М.:Просвещение, 1993.

Бунимович Е. А., Булычёв В.А. Вероятность и статистика. 5-9 классы: Пособие для общеобразовательных учебных заведений, — М.:Дрофа , 2005.

Виленкин Н. Я. и другие. Алгебра и математический анализ для 10 класса: Учебное пособие для учащихся школ и классов с углублённым изучением математики. — М.:Просвещение,1992.

Виленкин Н. Я. и другие. Алгебра и математический анализ для 11 класса: Учебное пособие для учащихся школ и классов с углублённым изучением математики — М.:Просвещение, 1990.

Глейзер Г.И. История математики в школе: 9-10 класс. Пособие для учителей. — М.: Просвещение 1983.

Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Математика 9:Алгебра. Функции. Анализ данных — М.: Дрофа, 2000.

Колягин и другие. Алгебра и начала анализа 11 класс. Математика в школе — 2002 — №4 — с.43,44,46.

Люпшкас В.С. Факультативные курсы по математике: теория вероятностей: Учебное пособие для 9-11 классов.- М.,1991.

Макарычев Ю.Н., Миндюк Н.Г. Элементы статистики и теории вероятностей: Учебное пособие для учащихся 7-9 классов.- М.: Просвещение, 2005.

Мордкович А.Г., Семенов П.В. Алгебра и начала анализа 10 класс: Учебник для общеобразовательных учреждений (профильный уровень) – М.: Мнемозина, 2005.

Ткачева М.В., Федорова Н.Е. Элементы статистики и вероятность: Учебное пособие для учащихся 7-9 классов.- М.: Просвещение, 2005.

infourok.ru