Нахождение дроби от числа и числа по его дроби

Нахождение дроби от числа выполняется тогда, когда известно некоторое число, но не известна часть числа, которая выражена количеством долей от целого.

Так как дробь — это часть от числа, а число — натуральное или именованное число, то нахождение дроби от числа — это вычисление той части числа, которая определена только дробью.

Часть от числа находится умножением.

Правило. Чтобы найти дробь от числа , надо число умножить на эту дробь.

Если часть от числа — правильная дробь, то результат вычисления меньше заданного числа .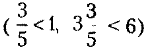

Если часть от числа — смешанная или неправильная дробь, то результат вычисления больше заданного числа .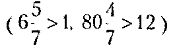

Нахождение числа по его дроби выполняется тогда, когда число неизвестно, но известна часть числа, которая выражена долями от целого.

Число по его части находится действием деления.

Правило. Чтобы найти число по его дроби , надо число представляющее дробь, разделить на эту дробь

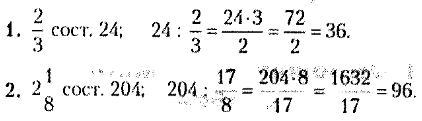
Если часть числа выражена правильной дробью, то результат вычисления больше заданного числа ( 24).

Если часть от числа представлена смешанной или неправильной дробью, то результат вычисления меньше заданного числа (2 > 1, 96 Тимур говорит:

В некоторых школьных учебниках, как и на вашем сайте, встречается тема «нахождение числа по его дроби». Такая постановка вопроса является неверной. И если, читая учебник 6 класса,можно предположить, что словом «дробь» не корректно подменяется понятие доля или часть, то после прочтения этой темы на вашем сайте становится ясно, что само понятие дроби дается не верно. Дробь не является частью числа вообще, дробь — это часть (или несколько частей) ЕДИНИЦЫ.

shkolo.ru

Как найти число по его дроби

Правило нахождения числа по его дроби:

Чтобы найти число по данному значению его дроби, нужно это значение разделить на дробь.

Рассмотрим, как найти число по его дроби, на конкретных примерах.

1) Найти число, 3/4 которого равны 12.

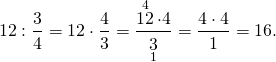
Чтобы найти число по его дроби, это число делим на эту дробь. Чтобы разделить число на дробь , надо данное число умножить на число, обратное к дроби (то есть на перевернутую дробь). Чтобы умножить дробь на число , надо числитель умножить на это число, а знаменатель оставить без изменения. Сокращаем 12 и 3 на 3. Так как в знаменателе получили единицу, ответ — целое число.

2) Найти число, если 9/10 его равняются 3/5.

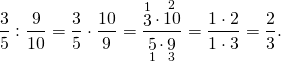
Чтобы найти число по данному значению его дроби, это значение делим на эту дробь. Чтобы разделить дробь на дробь, первую дробь умножаем на обратную ко второй (перевернутую). Чтобы умножить дробь на дробь, числитель умножаем на числитель, знаменатель — на знаменатель. Сокращаем 10 и 5 на 5, 3 и 9 — на 3. В результате получили правильную несократимую дробь, значит это — окончательный результат.

3) Найти число, 9/7 которого равны

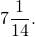
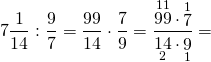
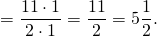
Чтобы найти число по значению его дроби, это значение делим на эту дробь. Смешанное число переводим в неправильную дробь и умножаем его на число, обратное ко второму (перевернутую дробь). Сокращаем 99 и 9 на 9, 7 и 14 — на 7. Поскольку получили неправильную дробь, необходимо выделить из нее целую часть.

www.for6cl.uznateshe.ru

Нахождение числа по его дроби

Если известно сколько составляет часть от целого, то по известной части можно «восстановить» целое.

Для этого пользуемся правилом нахождения целого (числа) по его дроби (части).

Чтобы найти число по его части, выраженной дробью, нужно данное число разделить на дробь.

Пример. Рассмотрим задачу.

Поезд прошёл 240 км, что составило

всего пути. Какой путь должен пройти поезд?

Решение. 240 км — часть всего пути. Эти же километры выражены дробью 15/23 от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части, и 15 таких частей составляют 240 км (числитель дроби равен 15 ).
Значит, можно найти, сколько составляет

Значит, чтобы найти весь путь ( 23 части, каждая из которых по 16 км) нужно:

Кратко запись решения такой задачи можно сделать следующим образом.

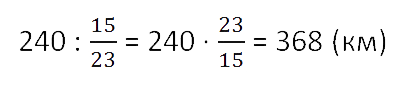
Ответ: поезд должен пройти 368 км.

Сложные задачи на нахождение числа по его части

Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в несколько действий.

При подготовке к диктанту по английскому языку Оля выучила четверть всех слов , заданных учителем. Если бы она выучила ещё 4 слова , то была бы выучена треть всех слов . Сколько всего слов надо было выучить Оле?

Решение. Как обычно подчеркнём в условии задачи все важные данные.

Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде разности дробей.

math-prosto.ru

«Нахождение дроби от числа». Математика. 6-й класс

Разделы: Математика

Цели:

  1. Ввести понятие дроби от числа, правила нахождения дроби от числа, ознакомление учащихся с новым типом задач на нахождение дроби от числа. Дать четкое понятие структуры данных задач, состоящей из трех составляющих: всё число, значение дроби, дробь.
  2. Развитие умения анализировать, делать выводы, развитие вычислительных навыков.
  3. Воспитание познавательного интереса к предмету путем применения новейших технологий обучения, воспитание самоконтроля и взаимоконтроля.

Задача урока:

Материализацией умственной деятельности при прохождении данной темы в виде выделенных отдельных шагов – операций действия и видимой схемы действия – таблицы трех составляющих, добиться четкого понятия структуры задач на нахождение дроби от числа, а также последующих тем на нахождение числа по его дроби и на нахождение дроби-части, которую одно число составляет от другого и умения распознавать эти задачи, выполнять соответствующие преобразования. Применение компьютерных технологий облегчает выполнение этой задачи, так как после урока, уже не имея материализованной опоры перед глазами, остается ориентация на наглядные приведенные таблицы и рисунки.

Оборудование: компьютер, мультимедийный проектор, доска, файл презентации.

Учебник: математика. 6-й класс: учебник для общеобразоват. учреждений / Н.Я. Виленкин и др., -М.: Мнемозина, 2007. 288 с.: ил.

ХОД УРОКА

1. Проверка домашнего задания. Устная проверка № 474. Решение № 478 (а, в) записано учеником на доске во время перемены.

2. Устная работа (слайд № 1. Презентация). а) Повторение умножения обыкновенных дробей; б) повторение понятия процента и его представления в виде десятичной дроби.

3. Постановка проблемы (слайд № 2).

а) Задача: Обезьянке в зоопарке утром на завтрак дали пучок из шести бананов. Она съела 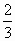пучка. Сколько бананов съела обезьянка?

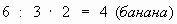
Итак, обезьянка съела 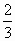от всего пучка, то есть 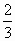от 6 бананов.

Записывают 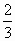от 6.

Читают “дробь 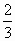от числа 6”

Сегодня учимся находить дробь от числа. В тетрадях записывается тема “Нахождение дроби от числа”, переписывается с доски в тетрадь запись:

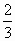“ от 6 ”
дробь число

с поясняющими надписями “дробь”, “число”. Объявляется, что ответ задачи “4 банана” — это значение дроби.

“ 4 — значение дроби ”

Итак, сегодня мы решаем задачи на нахождение дроби от числа.

б) Постановка вопроса (слайд № 3): можно ли решение рассмотренной задачи записать в виде другого выражения?

Ставится наводящий вопрос в случае затруднения: “Какие действия с обыкновенными дробями мы научились выполнять?”.

Ожидаемый ответ: 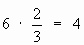. После чего, на слайде происходит анимированное преобразование первоначального решения.

Далее учащиеся приходят к выводу, что дробь от числа находится умножением и формулируется правило.

4. Объяснение новой темы. Читаем правило в учебнике, проговариваем хором. № 486 (а, б, в, г):

а) решает учитель с комментариями, б), в), г) учащиеся на доске с повторением правила. Ответы оцениваются.

5. Физкультминутка.

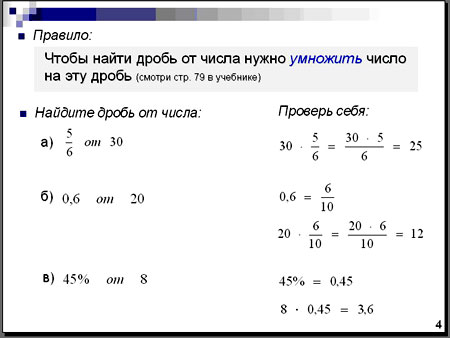
6. Закрепление (слайд № 4). А) Повторяется правило на слайде и рассматриваются 3 примера, в которых “дробь” представлена в трех вариантах: обыкновенная дробь, десятичная дробь и проценты. После обсуждения решения, учащиеся приступают к самостоятельному выполнению задания. Далее проводится обмен тетрадей в парах и проверка решения соседа по парте по появившемуся решению на слайде и самооценка работы по объявленному критерию. Выборочно проставляются оценки.

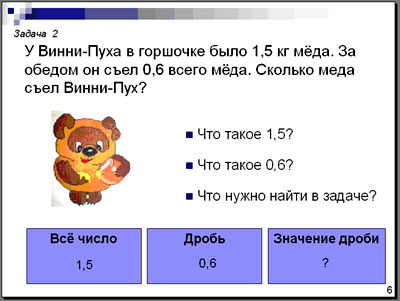
б) Закрепление распознавания трех составляющих “все число”, “дробь”, “значение дроби” в задачах на нахождение дроби от числа. (слайды № 5, № 6, № 7) Рассматриваются три задачи с обсуждением данных понятий. Обращается внимание учащихся на то, что во второй задаче “все число” — десятичная дробь, в третьей задаче — “дробь” больше 1. Для решения задач вызываются к доске трое учащихся. Таблицы трех составляющих остаются на слайде. Решение проверяется по слайду. После оформления решения учащимися на доске, ответы проверяются по слайду. Ответы оцениваются.

7. Домашнее задание: № 523, № 526.

8. Подведение итогов (слайд № 9).

xn--i1abbnckbmcl9fb.xn--p1ai

Нахождение части числа и числа по его части

В процессе решения задач 149–156 надо подвести учащихся к пониманию правила нахождения части числа:

Чтобы найти часть числа, выраженную дробью, можно это число разделить на знаменатель дроби и полученный результат умножить на ее числитель.

Разумеется, это правило учащиеся могут формулировать лишь для конкретных ситуаций: чтобы найти 3 /4 числа 24, можно это число разделить на знаменатель дроби 4 и полученный результат умножить на числитель 3.

149. а) На ветке сидели 12 птиц; 2 /3 их числа улетели. Сколько птиц улетело?

б) В классе 32 учащихся; 3 /4 всех учащихся каталось на лыжах. Сколько учащихся каталось на лыжах?

150. а) Велосипедисты за два дня проехали 48 км. В первый день они проехали 2 /3 всего пути. Сколько километров они проехали во второй день?

б) Некто, имея 350 рублей, потратил 5 /7 своих денег. Сколько денег у него осталось?

в) В тетради 24 страницы. Девочка исписала 5 /8 числа всех страниц тетради. Сколько осталось неисписанных страниц?

151. Старинная задача. Купивши комод за 36 р., я потом вынужден был продать его за 7 /12 цены. Сколько рублей я потерял при этой продаже?

152. Автотуристы за три дня проехали 360 км; в первый день они проехали 2 /5, а во второй день — 3 /8 всего пути. Сколько километров проехали автотуристы в третий день?

153. 1) В драмкружке занимаются 24 девочки и несколько мальчиков. Число мальчиков составляет 3 /8 числа девочек. Сколько учащихся занимается в драмкружке?

2) В коллекции имеется 45 юбилейных рублевых монет. Число 3-х и 5-ти рублевых монет составляет 2 /9 числа рублевых монет. Сколько всего юбилейных монет в 1, 3 и 5 рублей в коллекции?

Задачи 154–156 учащиеся должны решать, находя сначала указанную часть величины, а потом увеличивая или уменьшая эту величину на найденную часть. Другой способ решения будет показан позже.

154. 1) Уменьшите 90 рублей на 1 /10 этой суммы.

2) Увеличьте 80 рублей на 2/5 этой суммы.

155. В прошлом месяце цена товара составляла 90 р. Теперь она понизилась на 3 /10 этой суммы. Какова теперь цена товара?

156. В прошлом месяце зарплата составляла 400 р. Теперь она увеличилась на 2 /5 этой суммы. Какова теперь зарплата?

В процессе решения задач 157–158 и следующих задач нужно подвести учащихся к пониманию и правильному применению правила нахождения числа по его части:

Чтобы найти число по его части, выраженной дробью, можно эту часть разделить на числитель дроби и полученный результат умножить на ее знаменатель.

Формулировка этого правила сложна из-за необходимости
как-то называть число, которое у нас названо «частью». Эту трудность вынуждены обходить и авторы учебников. Так в учебнике И.В. Барановой и З.Г. Борчуговой правило формулируется лишь для конкретных случаев: чтобы найти число, 3 /5 которого составляют 90 км, надо 90 км разделить на числитель дроби 3 и полученный результат умножить на знаменатель дроби 5. [3]

Именно в таком виде им могут пользоваться учащиеся. Правда, говоря о числе, лучше не использовать наименований, так как число и величина не одно и то же. Позднее в том же учебнике на с. 226 формулируется общее правило, в котором применяемому нами термину «часть» соответствует оборот «число, ей соответствующее», что вряд ли проще.

157. а) 120 р. составляют 3 /4 имеющейся суммы денег. Какова эта сумма?

б) Определите длину отрезка, 3 /5 которого равны 15 см.

158. а) Сыну 10 лет. Его возраст составляет 2 /7 возраста отца. Сколько лет отцу?

б) Дочери 12 лет. Ее возраст составляет 2 /5 возраста матери. Сколько лет матери?

На покупку овощей хозяйка израсходовала 6 р., что составило 1 /6 имевшихся у нее денег. Затем она купила 2 кг яблок по 7 р. за килограмм. Сколько денег у нее осталось после этих покупок?

160. Отец купил сыну костюм за 24 р., на что израсходовал 1 /3 своих денег. После этого он купил несколько книг, и у него осталось 39 р. Сколько стоили книги?

161. Сыну 8 лет, его возраст составляет 2 /9 возраста отца. А возраст отца составляет 3 /5 возрастадедушки. Сколько лет дедушке?

162.* Из папируса Ахмеса (Египет, ок. 2000 г. до н. э.).

Приходит пастух с 70 быками. Его спрашивают:

— Сколько приводишь ты из своего многочисленного стада?

— Я привожу две трети от трети скота. Сочти!

www.shevkin.ru