В генераторах электрического тока, с которыми мы знакомились до сих пор – электростатических машинах, гальванических элементах (§ 75), аккумуляторах (§ 79) и термоэлементах (§ 83), – э. д. с. с течением времени не меняла своего направления: положительный электрод всегда оставался положительным, отрицательный – отрицательным, и ток во внешней цепи постоянно шел в одном и том же направлении: от положительного электрода к отрицательному. Такой ток называют прямым или постоянным. До тех пор, пока не происходило никаких внутренних изменений в самом генераторе, т. е. пока не сказывались, например, явления поляризации электродов в гальванических элементах, или не менялась скорость вращения электростатической машины, или не менялась температура между спаями термоэлемента, оставалась постоянной и э. д. с., а стало быть, и напряжение на зажимах генератора и сила тока в цепи.

Напротив, в генераторах, установленных на электростанциях и дающих ток, которым мы пользуемся для освещения, приведения в действие электродвигателей (моторов) и для других целей, всегда возникает переменная э. д. с., непрерывно изменяющая свое значение и много раз в секунду меняющая свое направление. С некоторыми деталями устройства этих генераторов мы познакомимся в следующей главе, но для понимания того, каким образом в них создается переменная э. д. с., нам необходимо уже сейчас выяснить основной принцип их устройства.

В современной технике применяются почти исключительно индукционные генераторы, т. е. машины, в которых э. д. с. возникает в результате процесса электромагнитной индукции. Основная схема устройства такого генератора, на которой видны все принципиально важные его детали, показана на рис. 288. Между полюсами сильного магнита 1, т. е. в магнитном поле, вращается проволочная рамка 2 концы которой припаяны к кольцам 3 и 4, вращающимся вместе с рамкой; к этим кольцам прижимаются пружинящие пластинки 5 и 6 (так называемые щетки), от которых идут провода к внешней цепи. При вращении рамки в магнитном поле пронизывающий ее магнитный поток все время изменяется и, следовательно, в рамке возникает индуцированная э. д. с. Таким образом, процесс, происходящий во всех промышленных генераторах тока, это – повторение в гигантских масштабах основного индукционного опыта Фарадея, который мы рассмотрели в § 138.

Рис. 288. Модель индукционного генератора

Рассмотрим теперь подробнее, какова будет возникающая в рамке индуцированная э. д. с. Для простоты будем считать магнитное поле, в котором вращается рамка, однородным. Магнитный поток через рамку (§ 138) есть произведение магнитной индукции поля на площадь рамки и на синус угла между плоскостью рамки и направлением поля:

.

Если рамка вращается равномерно и совершает полный оборот за время , то за единицу времени рамка поворачивается на угол . Поэтому, если время отсчитывать от того момента, когда рамка стояла параллельно линиям поля, то значение угла в некоторый момент времени будет равно . Обозначая частоту вращения рамки, т. е. число ее оборотов в единицу времени, буквой , а угловую скорость (см. том I) буквой , можно написать:

, .

.

Подставив это выражение в формулу для магнитного потока, мы увидим, что закон его изменения с течением времени имеет вид

. (151.1)

График, изображающий зависимость магнитного потока через рамку от времени, представляет собой синусоиду (рис. 289,а). Магнитный поток меняет свой знак два раза за каждый оборот рамки, обращаясь в нуль в те моменты, когда она параллельна направлению поля, и достигая максимальных значений (того или иного знака) в моменты, когда она перпендикулярна к полю.

Рис. 289. График изменения с течением времени мгновенных значений: а) магнитного потока ; б) индуцированной э. д. с. в опыте, изображенном на рис. 288

Индуцированная в рамке э. д. с. определяется не значением самого магнитного потока, а скоростью его изменения, т. е. величиной (§ 141). Нетрудно видеть, что и эта величина не остается постоянной, а все время изменяется при вращении рамки. На рис. 289,а показаны изменения магнитного потока за одинаковые промежутки времени для момента , когда , и для момента , когда имеет максимальное значение. Первое значение гораздо больше второго, и, следовательно, мгновенное значение индуцированной э. д. с. в момент имеет максимальное значение, а по мере вращения рамки убывает, достигая нулевого значения к моменту .

При дальнейшем повороте рамки э. д. с. меняет свой знак. Действительно, по правилу Ленца (§ 139) индуцированная э. д. с. всегда направлена так, чтобы магнитное поле создаваемого ею тока тормозило процесс, вызывающий индукцию. Поэтому в течение первой четверти периода, когда магнитный поток через рамку возрастает, поле индукционного тока должно ослаблять внешнее поле, а в течение следующей четверти периода, когда магнитное поле убывает, оно должно усиливать это поле. Отсюда ясно, что в моменты прохождения э. д. с. через нуль должно происходить изменение ее знака.

На рис. 289,б графически показана зависимость мгновенных значений индуцированной э. д. с. от времени. Можно показать, что эта кривая, как и график магнитного потока, представляет собой синусоиду, но только смещенную на четверть периода по отношению к синусоиде, изображающей изменение магнитного потока.

Действительно, для момента поток , для момента поток . Следовательно, за время изменение потока

.

Согласно известной теореме тригонометрии это выражение можно представить в виде

.

Если очень мало, то , a . Итак, изменение потока за малое время

.

Следовательно, э. д. с., равная , есть

,

т. е. действительно выражается синусоидой той же частоты, но сдвинутой на (четверть периода).

Само собой разумеется, что по такому же закону синусоиды изменяется и мгновенное значение напряжения и на зажимах машины или между двумя любыми точками сети. Графики изменения этой величины имеют такой же вид, как и приведенные на рис. 289 графики индуцированной э. д. с. Говорят, что такого рода кривые воспроизводят «форму» переменного напряжения. Ток, возникающий под влиянием переменного напряжения, также будет переменным, и «форма» его подобна «форме» напряжения.

Не только в нашей модели, но и в машинах, применяемых в электротехнике, в подавляющем большинстве случаев имеют дело с напряжениями и токами, которые можно считать синусоидальными. Закон изменения мгновенных значений этих величин со временем выражается формулами

, , (151.2)

причем через и обозначены максимальные значения напряжения и тока.

sernam.ru

По какому закону эдс постоянная

Рассмотрим переходные процессы в цепи, содержащей последовательно соединенные резистор R и индуктивность L . Уравнение Кирхгофа для такой цепи

,

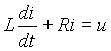где u = u(t ) — напряжение на входе цепи. Найдем решение этого уравнения для свободной составляющей тока, т.е. при u = 0, в виде i с = Ie pt . Для этого подставим выражение для тока в исходное уравнение и найдем значение p

.

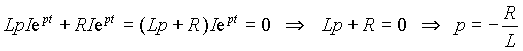Выражение Lp + R=0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных тока на p k , где k — порядок производной.

Таким образом, общее решение для тока при переходном процессе в R-L цепи можно представить в виде

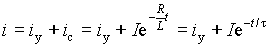
где t = 1/|p| = L/R — постоянная времени переходного процесса; I — постоянная интегрирования, определяемая по начальным значениям; i — установившийся ток в цепи, определяемый по параметрам R и L и напряжению на входе u.

Длительность переходного процесса в цепи, определяемая значением t , возрастает с увеличением L и уменьшением R.

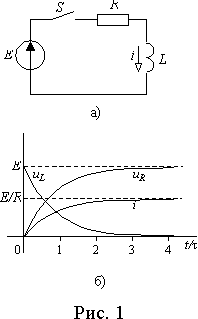
Рассмотрим подключение R—L цепи к источнику постоянной ЭДС E (рис. 1 а)).

Установившийся ток в этой цепи будет определяться только ЭДС E и резистивным сопротивлением R , т.к. после окончания переходного процесса i = const и uL = Ldi/dt = 0, т.е. i у = E/R .

Полный ток в переходном процессе из выражения (1)

.

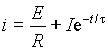Для определения постоянной I найдем начальное тока. До замыкания ключа ток очевидно был нулевым, а т.к. подключаемая цепь содержит индуктивность, ток в которой не может измениться скачкообразно, то в первый момент после коммутации ток останется нулевым. Отсюда

.

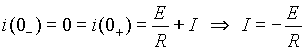Подставляя найденное значение постоянной I в выражение для тока, получим

.

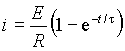Из этого выражения можно определить падения напряжения на резисторе uR и индуктивности uL

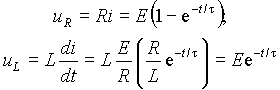
Из выражений (1)-(3) следует, что ток в цепи нарастает по экспоненте с постоянной времени t = L/R от нулевого до значения E/R (рис. 1 б)). Падение напряжения на сопротивлении uR повторяет кривую тока в измененном масштабе. Напряжение на индуктивности uL в момент коммутации скачкообразно возрастает от нуля до E , а затем снижается до нуля по экспоненте (рис. 1 б)).

Подставляя выражения (3) в уравнение Кирхгофа для цепи после коммутации, можно убедиться в его справедливости в любой момент времени

.

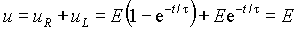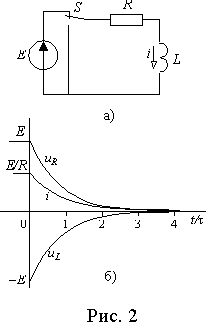
Пусть рассмотренная выше R—L цепь длительное время была подключена к источнику ЭДС E, а затем замкнута накоротко (рис. 2 а)).

В этом случае установившийся ток будет равен нулю и задача сводится к отысканию его свободной составляющей. Из выражения (1)

.

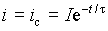Постоянную I можно определить из начальных условий. Установившийся ток в цепи до переключения ключа S был равен i(0 — ) = E/R , а т.к. в первый момент после коммутации ток в индуктивности сохраняет свое значение, то i(0 — ) =i(0+) = I = E/R . Отсюда ток и падения напряжения в цепи

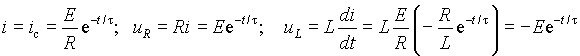
Из выражений (4) следует, что при замыкании цепи накоротко ток уменьшается от E/R до нуля по экспоненте с постоянной времени t = L/R (рис. 2 б)). Падение напряжения на резисторе изменяется по такому же закону, а напряжение на индуктивности в момент коммутации скачком изменяется от нуля до — E , а затем снижается до нуля ( рис. 2б)).

Общее падение напряжения на резисторе и индуктивности в любой момент времени

,

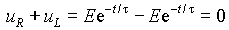как и следовало ожидать, равно нулю и в переходном процессе происходит преобразование энергии магнитного поля в тепло.

При отключении цепи содержащей индуктивность в ней могут возникать падения напряжений опасные для ее элементов. Пусть R—L цепь с подключенным к ней вольтметром отключается от источника постоянной ЭДС E (рис. 3).

Так как цепь содержит индуктивность, то после размыкания ключа S ток не сможет изменить своего значения и будет протекать в контуре R—L—V . Значение тока до коммутации i(0 — ) = E/R = i(0+) = i (0) Уравнение Кирхгофа для этого контура

где RV — сопротивление вольтметра.

Обычно RV>>R , поэтому напряжение на вольтметре и на индуктивности в момент отключения превосходят ЭДС источника в RV/R раз. Это может быть опасным для вольтметра и изоляции катушки. Если индуктивность цепи достаточно велика, то запасенной в ней энергии может оказаться достаточно для разрушения изоляции или входных цепей прибора. Поэтому при отключении цепи постоянного тока с большой индуктивностью ее предварительно замыкают на малое сопротивление, а измерительные приборы отключают .

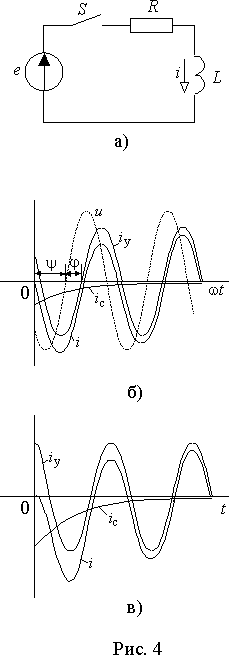
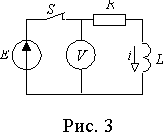
Рассмотрим теперь процесс подключения R—L цепи к источнику переменной синусоидальной ЭДС (рис. 4 а)).

Ток после коммутации в соответствии с выражением (1)

.

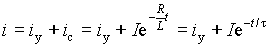de.ifmo.ru

Журнал «Квант»

Генератор переменного тока

Электрические машины, преобразующие механическую энергию в электрическую, называют генераторами. В современной энергетике применяют индукционные генераторы переменного тока, в которых используется явление электромагнитной индукции. Они позволяют получать большие токи при достаточно высоком напряжении.

Простейшей моделью такого генератора может служить рамка abcd (рис. 1), вращающаяся в однородном магнитном поле вокруг своей оси ОО’, перпендикулярной индукции магнитного поля.

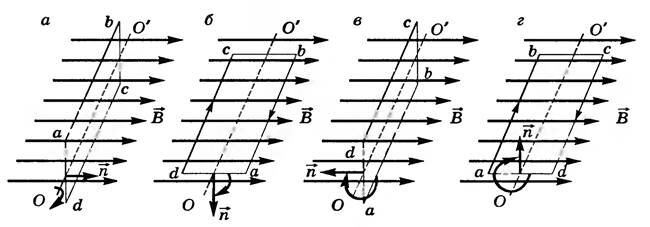
Пусть в начальный момент времени t = 0 плоскость рамки перпендикулярна вектору магнитной индукции (рис. 1, а), ее пронизывает максимальный магнитный поток \(

\Phi_m \left( \alpha = 0\right).\) При равномерном вращении рамки пронизывающий ее магнитный поток уменьшается. Вследствие этого, согласно закону электромагнитной индукции, в рамке возникает ЭДС индукции \(

\varepsilon_i.\) Когда плоскость рамки станет параллельна вектору индукции магнитного поля (рис. 1, б), пронизывающий ее магнитный поток станет равным нулю \(

\left( \Phi = 0, \alpha = \frac <\pi>2\right).\) Скорость же изменения магнитного потока при прохождении рамки через это положение наибольшая, так как проводники рамки аЬ и cd движутся в этот момент перпендикулярно линиям индукции. Возникающая ЭДС индукции, пропорциональная скорости изменения магнитного потока, будет максимальная, и создаваемый ею в этом случае индукционный ток направлен (согласно правилу правой руки) от Ь к a и от d к с. При дальнейшем повороте рамки магнитный поток увеличивается, ЭДС, не изменяя своего знака, будет уменьшаться по величине и в положении (рис. 1, в) \(

\Phi = \Phi_0, \frac <\Delta \Phi> <\Delta t>= 0,\) так как при прохождении через это положение проводники витка аЬ и cd скользят вдоль линии поля, не пересекая их. Следовательно, ЭДС индукции, возникающая в контуре в этом случае, \(

\varepsilon_i = 0.\) При дальнейшем вращении рамки магнитный поток уменьшается. Скорость изменения магнитного потока увеличивается и ЭДС индукции возрастает. Согласно рисунку 1, г \(

\left | \varepsilon_i \right | = \left | \varepsilon_ \right |,\) но направление индукционного тока в витках (согласно правилу правой руки) совпадает с направлением от a к и от с к d (противоположно таковому на рис. 1, б). Это направление будет сохраняться и при дальнейшем движении рамки и начнет убывать, так как магнитный поток хотя и увеличивается, но скорость изменения его уменьшается.

При последующих оборотах рамки все эти явления будут повторяться вновь. Таким образом, ЭДС индукции во вращающейся рамке за один оборот изменяется от \(

Выясним, по какому закону будет изменяться ЭДС индукции в рамке площадью S, если рамка вращается с постоянной угловой скоростью ω (ω = const) в однородном магнитном поле с индукцией \(

\vec B \) вокруг оси, расположенной в плоскости рамки и перпендикулярной вектору \(

За время t рамка повернется на угол \(

\varphi = wt,\) и угол между нормалью к рамке и вектором магнитной индукции будет \(

\alpha = wt.\) Магнитный поток, пронизывающий рамку, в момент времени t равен \(

Согласно закону Фарадея, мгновенное значение ЭДС индукции, возникающей в рамке, равно первой производной магнитного потока по времени \(

\varepsilon_i = — \Phi’.\) Поэтому

\varepsilon_i = wBS \sin wt = \varepsilon_0 \sin wt,\)

\varepsilon_0 = wBS \) — амплитудное значение ЭДС, которое, как видно, тем больше, чем быстрее вращается рамка, чем больше площадь рамки, тем больше магнитная индукция поля.

Таким образом, при равномерном вращении рамки в однородном магнитном поле в ней возникает синусоидальная ЭДС с частотой колебаний, равной частоте вращения рамки, которая будет создавать синусоидальный ток в цепи той же частоты, но фаза колебания тока не обязательно должна совпадать с фазой изменения ЭДС. Поэтому в общем случае мгновенное значение силы тока \(

I = I_0 \sin \left( wt + \varphi,\right)\) где \(

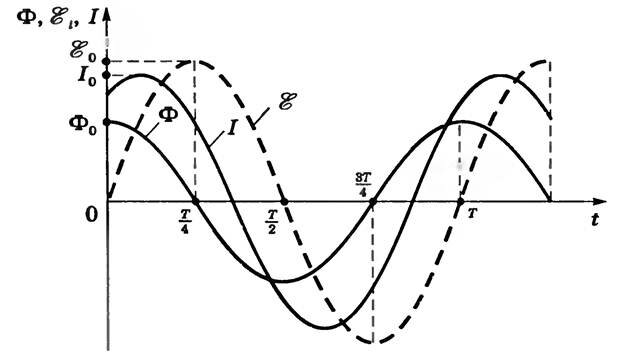
\varphi \) — разность фаз между колебаниями силы тока и ЭДС (рис. 2).

Чтобы использовать переменный ток, рамки соединяют с двумя изолированными кольцами, к кольцам прижимают щетки, к которым присоединяют контакты внешней цепи (рис. 3).

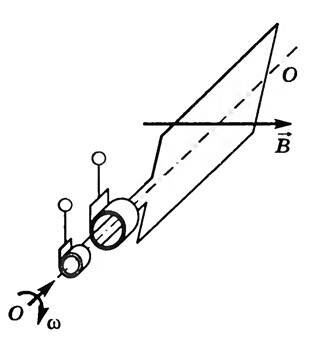
Мы рассмотрели принцип работы генератора переменного тока. Устройство генератора переменного тока гораздо сложнее. В настоящее время имеется много различных типов индукционных генераторов. Однако в каждом из них есть одни и те же основные части: 1) электромагнит (или постоянный магнит), создающий магнитное поле. Он называется индуктором;

2) обмотка, в которой индуцируется ЭДС. Эта часть носит название якорь;

3) состоящий из металлических колец коллектор;

4) щетки, соединяющие неподвижные проводники с вращающимися проводниками.

Неподвижная часть генератора называется статором. В описанном случае статором является индуктор. Подвижная часть генератора — ротор. В рассмотренном случае ротором является якорь. Для получения ЭДС индукции важно относительное перемещение проводника и магнитного поля. Поэтому на практике индуктор делают вращающимся, а якорь — неподвижным. Это вызвано тем, что с помощью подвижных контактов практически невозможно отводить от генератора токи высокого напряжения (большой амплитуды) из-за сильного искрения в подвижных контактах. Индуктором же является электромагнит, для питания которого нужен сравнительно слабый постоянный ток, и при таком слабом токе скользящие контакты хорошо работают.

Для того чтобы увеличить амплитуду ЭДС, необходимо увеличить магнитный поток через витки якоря. А это можно сделать, сконцентрировав магнитный поток в том месте, где находится якорь. Поэтому магнитную систему генератора изготавливают в виде замкнутой цепи, состоящей из двух сердечников, сделанных из железа. Обмотки индуктора размещены в пазах одного из сердечников, а обмотки якоря — в пазах другого. Один из сердечников, обычно внутренний, вращается вместе с индуктором. Другой сердечник с якорем в пазах неподвижен (статор). Зазор между сердечниками статора и ротора делают как можно уже. Этим достигается наибольшее значение потока магнитной индукции.

Сердечники изготавливают из тонких изолированных друг от друга железных пластин, чтобы уменьшить токи Фуко (см. Закон электромагнитной индукции), при протекании которых происходит нагревание сердечников.

Для увеличения амплитудного значения ЭДС индукции якорь изготавливают из большого числа витков. Амплитуда возникающей ЭДС индукции будет равна в этом случае \(

\varepsilon_0 = N \Phi_0 w,\) где N — число витков.

Когда у ротора имеется одна пара магнитных полюсов, то частота вращения совпадает с частотой переменного тока. В нашей стране и странах СНГ используется промышленный переменный ток частотой 50 Гц. В случае N пар полюсов частота переменного тока в N раз больше частоты вращения ротора. Одну пару полюсов делают у турбогенераторов, роторы которых приводятся во вращение паровой турбиной, а тихоходные многополюсные генераторы устанавливаются на гидростанциях. Так, на Братской ГЭС — 24, на Волжской ГЭС — 44, на Угличской на Волге — 48 пар полюсов.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 396-399.

www.physbook.ru

Закон электромагнитной индукции. ЭДС индукции в движущихся проводниках.

ЭДС индукции в проводниках, которые движутся в постоянном магнитном поле, соответствует 2му типу электромагнитной индукции, который обусловлен не переменным внешним магнитным полем, а действием сил Лоренца на свободные заряды проводника.

ЭДС индукции, которая возникает на концах проводника имеющего длину l, и который движется с постоянной скоростью v под определнным углом α к вектору индукции однородного магнитного поля, равна:

.

где A — работа силы Лоренца по перемещению заряда q на пути l, FL — сила Лоренца, которая действу­ет на заряд, что движется.

Если такой проводник является частью замкнутой цепи, осталь­ные части которой неподвижны, то в цепи образуется электрический ток.

.

где R — сопротивление нагрузки (лампочки); r — сопротивление проводника, который играет роль внутреннего сопротивления источни­ка тока (сопротивлением соединяющих проводников пренебрегаем).

С другой стороны, эту же ЭДС индукции можно получить, применив основной закон электромагнитной индукции:

.

В этом случае изменение потока происходит не за счет изменения индукции поля, а за счет изменения площади контура, который равен ΔS = -lvΔt. В результате имеем:

www.calc.ru