Округление результатов измерений (по материалам СПб АСМС)

Правила записи чисел по СТ СЭВ 543 — 77

1. Значащие цифры данного числа — все цифры от первой слева, не равной нулю, до последней справа. При этом нули, следующие из множителя 10, не учитывают.

а) Число 12,0 имеет три значащие цифры.

б) Число 30 имеет две значащие цифры.

в) Число 120 . 10 имеет три значащие цифры.

г) 0,514 . 10 имеет три значащие цифры.

д) 0,0056 имеет две значащие цифры.

2. Если необходимо указать, что число является точным, после числа указывают слово «точно» или последнюю значащую цифру печатают жирным шрифтом. Например, в печатном тексте: 1 кВт . ч = 3600 Дж (точно).

3. Различают записи приближенных чисел по количеству значащих цифр.

а) Различают числа 2,4 и 2,40. Запись 2,4 означает, что верны только целые и десятые доли, истинное значение числа может быть, например, 2,43 и 2,38. Запись 2,40 означает, что верны и сотые доли: истинное значение числа может быть 2,403 и 2,398, но не 2,41 и не 2,382.

б) Запись 382 означает, что все цифры верны: если за последнюю цифру ручаться нельзя, то число должно быть записано 3,8 . 10 .

в) Если в числе 4720 верны лишь две первые цифры, оно должно быть быть записано 47 * 10 или 4,7 * 10 .

4. Число, для которого указывают допустимое отклонение, должно иметь последнюю значащую цифру того же разряда, как и последняя значащая цифра отклонения.

а) Правильно: 17,0 + 0,2. Неправильно: 17 + 0,2 или 17,00 + 0,2.

б) Правильно: 12,13 + 0,17. Неправильно: 12,13 + 0,2.

в) Правильно: 46,40 + 0,15. Неправильно: 46,4 + 0,15 или 46,402 + 0,15.

5. Числовые значения величины и её погрешности (отклонения) целесообразно записывать с указанием одной и той же единицы величины.

6. Интервалы между числовыми значениями величин целесообразно записывать:

от 60 до 100, свыше 120 до 150.

Правила округления чисел по СТ СЭВ 543 — 77

1. Округление числа представляет собой отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда.

2. В случае, если первая из отбрасываемых цифр (считая слева направо) менее 5, то последнюю сохраняемую цифру не меняют.

Пример: Округление числа 12,23 до трех значащих цифр дает 12,2.

3. В случае, если первая из отбрасываемых цифр (считая слева направо) равна 5, то последнюю сохраняемую цифру увеличивают на единицу.

Пример: Округление числа 0,145 до двух цифр дает 0,15.

Примечание. В тех случаях, когда следует учитывать результаты предыдущих округлений, поступают следующим образом.

Если отбрасываемая цифра получена в результате округления в меньшую сторону, то последнюю оставшуюся цифру увеличивают на единицу (с переходом при необходимости в следующие разряды).

Пример: Округление числа 0,25 (полученного в результате предыдущего округления числа 0,252) дает 0,3 .

4. В случае, если первая из отбрасываемых цифр (считая слева направо) более 5, то последнюю сохраняемую цифру увеличивают на единицу.

Пример: Округление числа 0,156 до двух значащих цифр дает 0,16.

Округление выполняют сразу до желаемого количества значащих цифр, а не по этапам.

Пример: Округление числа 565,46 до трех значащих цифр дает 565.

6. Целые числа округляют по тем же правилам , что и дробные.

Пример: Округление числа 23456 до двух значащих цифр дает 23* 10 .

Из книги Л.И. Любимов, И.Д. Форсилова, Е.З. Шапиро

«Поверка средств электрических измерений. Справочная книга».

Ленинград, Энергоатомиздат, Ленинградское отделение, 1987 год

стр. 47 . 2.7. Правила округления и записи результатов измерений

Погрешность результата измерений позволяет определить те цифры результата, которые являются достоверными. Нецелесообразно удерживать в выражении для измеренного значения физической величины большое число цифр, т.к. цифры младших разрядов могут оказаться недостоверными.

Существуют определенные правила округления.

1. В выражении погрешности удерживается не более двух значащих цифр, причем последняя цифра обычно округляется до нуля или пяти. Две цифры следует обязательно удерживать в том случае, когда цифра старшего разряда менее 3.

2 . Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.

Пример. 235,732 + 0,15 округляется до 235,73 + 0,15, но не до 235,7 + 0,15.

При промежуточных вычислениях целесообразно, чтобы используемые числа содержали на одну значащую цифру больше, чем будет в окончательном результате. Это позволяет уменьшить погрешность от округления.

3. Если первая из отбрасываемых цифр (считая слева направо) меньше пяти, то остающиеся цифры не меняются.

Пример. 442,749 + 0,4 округляется до 442,7 + 0,4.

4. Если первая из отбрасываемых цифр больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.

Пример. 37,268 + 0,5 округляется до 37,3 + 0,5; 37,253 + 0,5 округляется до 37,3 + 0,5.

5. Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление может привести к ошибкам.

Пример. Поэтапное округление результата измерения 220,46 + 4 дает на первом этапе 220,5 + 4 и на втором 221 + 4, в то время как правильный результат округления 220 + 4.

Особенно внимательно нужно относиться к записи результата измерения без указания погрешности (что в общем случае крайне нежелательно). В этом случае в записываемом числе оставляются только те цифры, за достоверность которых можно ручаться, т.е. все значащие цифры записанного числа должны быть достоверными. Значащими цифрами числа считаются все цифры от первой слева, не равной нулю, до последней записанной справа цифры, при этом нули, записанные в виде множителя 10 в степени п, не учитываются. Поэтому записи 2,4 х 10 В в степени 3 и 2400 В не являются тождественными. Первая запись означает, что верны цифры тысяч и сотен вольт и истинное значение может быть, например, 2,42 или 2,38 кВ. Запись 2400 В означает, что верны и единицы вольт, истинное значение может быть 2400,2 или 2390,8 В, но не 2420 или 2380 В.

Из книги П.В. Новицкий и И.А. Зограф

«Оценка погрешностей результатов измерений»

Ленинград, Энергоатомиздат, Ленинградское отделение, 1991 год

стр. 25 1 — 4. ПРАВИЛА ОКРУГЛЕНИЯ ЗНАЧЕНИЙ ПОГРЕШНОСТИ И РЕЗУЛЬТАТА ИЗМЕРЕНИЙ

Рассчитывая значения погрешности, особенно при пользовании электронным калькулятором, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчета являются нормируемые значения погрешности средств измерения, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна — две значащие цифры. При этом приходится учитывать следующее. Если полученное число начинается с цифр 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30 — 50 %), что недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, т. е. указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности.

Исходя из этого на практике установилось такое правило: если полученное число начинается с цифры, равной или большей 3, то в нем сохраняется лишь один знак; если же оно начинается с цифр, меньших 3, т. е. с цифр 1 и 2, то в нем сохраняют два знака. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5 % указываются два знака, но в числах 0,5; 4; 6 % указывается

В итоге можно сформулировать три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.

1 . Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, — если первая есть 3 и более.

2 . Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.

3 . Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним — двумя лишними знаками.

Пример . На вольтметре класса точности 2,5 с пределом измерений 300 В был получен отсчет измеряемого напряжения Х = 267,5 В.

Расчет погрешности удобнее вести в следующем порядке: сперва необходимо найти абсолютную погрешность, а затем — относительную. Абсолютная погрешность /\ (Х) = jo X к /100; при jo = 2,5 % и Х к = 300 В это даёт /\ (Х) = 2,5 х 300 / 100 = 7,5 В

8 В; относительная

jo = /\ o x 100 / X = 7,5 x 100 / 267,5 = 2,81 %

Так как первая значащая цифра значения абсолютной погрешности (7,5 В) больше трех, то это значение должно быть округлено по обычным правилам округления до 8 В, но в значении относительной погрешности (2,81 %) первая значащая цифра меньше 3, поэтому здесь должны быть сохранены в ответе два десятичных разряда и указано j ( x ) = 2,8 %. Полученное значение Х = 267,5 В должно быть округлено до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности , т. е. до целых единиц вольт.

Таким образом, в окончательном ответе должно быть сообщено: «Измерение произведено с относительной погрешностью j ( x ) = 2,8 % . Измеренное напряжение Х = (268 + 8) В или Х = 268 В + 8 В.

При этом более наглядно указать пределы интервала неопределенности измеренной величины в виде Х = (260 — 276) В или 260 В

www.metrologie.ru

Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «Так точнее» – считают они. Однако легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего.

Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов.

Правила округления

1. Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу.
   Примеры:

   243.871 ± 0.026 ≈ 243.87 ± 0.03;
   243.871 ± 2.6 ≈ 244 ± 3;
   1053 ± 47 ≈ 1050 ± 50.

   Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5.
   Примеры:

   8.337 (округлить до десятых) ≈ 8.3;
   833.438 (округлить до целых) ≈ 833;
   0.27375 (округлить до сотых) ≈ 0.27.

   Если первая из отбрасываемых цифр больше или равна 5 , (а за ней одна или несколько цифр отличны от нуля), то последняя из остающихся цифр увеличивается на единицу.
   Примеры:

   8.3351 (округлить дл сотых) ≈ 8.34;
   0.2510 (округлитьь до десятых) ≈ 0.3;
   271.515 (округлить до целых) ≈ 272.

   Если отбрасываемая цифра равна 5 , а за ней нет значащих цифр (или стоят одни нули), то последнюю оставляемую цифру увеличивают на единицу, когда она нечетная, и оставляют неизменной, когда она четная.
   Примеры:

   0.875 (округлить до сотых) ≈ 0.88;
   0.5450 (округлить до сотых) ≈ 0.54;
   275.500 (округлить до целых) ≈ 276;
   276.500 (округлить до целых) ≈ 276.

   Примечание.

   1. Значащими называют верные цифры числа, кроме нулей, стоящих впереди числа. Например, 0,00807 – в этом числе имеется три значащих цифры: 8, ноль между 8 и 7 и 7 ; первые три нуля незначащие.
      8.12 · 10 3 – в этом числе 3 значащих цифры.
   2. Записи 15,2 и 15,200 различны. Запись 15,200 означает, что верны сотые и тысячные доли. В записи 15,2 – верны целые и десятые доли.
   3. Результаты физических экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени. Нули, стоящие в начале или конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10 -3 и 2,34·10 5 . Подобная запись упрощает вычисления, особенно в случае формул, удобных для логарифмирования.

   teachmen.ru

   Метрология правила округления

   

   

   

   

   

   Это особенно важно при использовании компьютера или калькулятора, поскольку результаты выдаются с заведомо заданной разрядностью (5 или 9 десятичных знаков) и они гипнотизируют своей будто бы впечатляющей точностью. Однако входными данными, как правило, есть или имела выборка наблюдений, или нормированные значения погрешностей с одной или двумя значащими цифрами. Поэтому при любых расчетах нужно всегда находить погрешности полученной оценки и оставлять в округленном результате лишь 1-2 недостоверных десятичных знаков. Однако при оценке погрешности может оказаться недостоверной даже первая значащая цифра. В этом случае приходится учитывать следующее обстоятельство. Если первая значащая цифра есть 1 или 2, то отбрасывание второго десятичного знака приводит к очень большой ошибке ( до 30-50%). Но если первая значащая цифра, например, 9, то сохранение второго знака ( то есть указание оценки, например, в виде 0,94 вместо 0,9) является дезинформацией, поскольку началу данные не обеспечивают такую достоверность.

   Исходя из этого на практике установилось следующее правило.

   Если первая недостоверная цифра есть 1 или 2, то хранится и второй недостоверный знак; если же она 3 и более, то второй недостоверный знак опускается. Согласно этому правила установлены и нормированы значения погрешностей средств измерений: в числах 1,5 и 2,5% указываются два десятичных знака, но в числах 0,5; 4; 6% — лишь один знак.

   Изложенные правила округления формулируются таким образом:

   1. Округление любого результата расчетов или измерение должно
   проводиться согласно его погрешности, для чего одновременно
   с самым результатом должна быть оцененная и его погрешность.

   2. Результат округляется к тому же десятичного знака, которым
   заканчивается округленное значение его абсолютной погрешности.

   3. Если в полученной оценке недостоверная даже первая значащая
   цифра, то оценка указывается с двумя знаками, если первый с них
   есть 1 или 2, и с одним десятичным знаком, если он есть 3 или более.

   4. Округления проводится лишь в окончательном ответе, а все
   предыдущие расчеты выполняются не менее чем с одним лишним
   знаком.

   literaturki.net

   Правила округления результатов измерений

   Погрешность результата измерения физической величины дает представление о том, какие последние цифры в его числовом значении являются сомнительными. Поэтому нет смысла выражать погрешность более чем одной или двумя цифрами. В соответствии с установленными правилами погрешность выражается двумя значащими цифрами, если первая из них 1 или 2, и одной, начиная с цифры 3.

   Числовое значение результата измерения также следует округлять в соответствии с числовым разрядом значащей цифры погрешности, т.е. числовое значение результата измерения должно оканчиваться цифрой того же разряда или тем же десятичным знаком, которым оканчивается значение абсолютной погрешности. При этом, если старшая отбрасываемая цифра меньше 5, то предыдущая не изменяется. Если старшая отбрасываемая цифра больше или равна 5, но за ней имеются значащие цифры, то предыдущую (оставляемую) цифру увеличивают на единицу. Если отбрасываемая цифра 5 не имеет за собой значащих цифр, то предыдущая не изменяется, если она четная, и увеличивается на единицу, если она нечетная.

   Например, при погрешности ±0,01 приведенные результаты округляются следующим образом:

   1.214 — 1,21;
   1,2151 — 1,22;
   1.215 — 1,22;
   1,225 — 1,22.

   Следует осмотрительно относиться к округлениям, производимым в процессе вычислений. Рекомендуется производить округления в окончательном ответе, а вычисление производить с одним-двумя лишними знаками.

   www.teh-lib.ru

   Правила округлений и формы представления результатов измерений

   Исходя из практики в метрологии сложилось правило оценивать погрешности измерений сверху. Этот принцип означает, что лучше преувеличивать погрешность измерения, чем ее преуменьшать: в первом случае снижается качество измерения, во втором — возможно полное обесценивание всего измерения. Кроме того, исходными данными для расчета погрешностей измерений являются нормируемые значения погрешностей средств измерений, которые указываются всего с одной или с двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только одна-две значащие цифры.

   Исходя из выше сказанного на практике сложились следующие правила округления погрешностей измерений.

   1 Погрешности измерений округляются в большую сторону.

   2 В окончательной записи погрешность измерения принято выражать числом с одной или двумя значащими цифрами. Две цифры удерживают при наиболее точных измерениях, а также если цифра старшего разряда числа, выража-ющего погрешность, равна трем или меньше трех. При приближенном оценивании погрешности, если ее выражают числом с одной значащей цифрой, то цифру 9 не применяют; две значащие цифры сохраняют, если цифра старшего разряда меньше 3, при этом для младшего обычно применяют только цифру 5.

   Наряду с изложенными правилами округления при приближенном оценивании погрешности предложены (например, в работе ) более обоснованные, но и более сложные правила. Для устранения резких скачков относительной погрешности округления предложено каждую декаду возможных значений округляемой погрешности делить на три части: от 0,1 до 0,2; от 0,2 до 0,5 и от 0,5 до 1,0 — и в каждой из этих частей использовать свой шаг округления, соответственно равный 0,02; 0,05 и 0,1. Тогда ряд разрешенных к употреблению округленных значений погрешностей получает вид: 0,10-0,12-0,14-0,16-0,18-0,20-0,25-0,30-0,35-0,40-0,45-0,5-0,6-0,7-0,8-0,9-1,0. Бесспорное преимущество такого ряда состоит в том, что погрешность от округления на границах участков изменяется лишь от 5 до 10 %.

   Округления при обработке результатов наблюдений и при записи результатов измерений следует выполнять, руководствуясь лишь следующими правилами:

   1 Округлять результат измерения следует так, чтобы он оканчивался цифрой того же разряда, что и значение его погрешности. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует младшему разряду числового значения погрешности.

   2 Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют. Лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают.

   3 Если цифра старшего из отбрасываемых разрядов больше или равна 5, а за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.

   4 Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная.

   5 Округление производится лишь в окончательном ответе, а все предварительные проводят с одним-двумя лишними разрядами.

   Остановимся на тех стандартных правилах определения показателей точности измерений и представлений результатов измерений, которые регламентируются ГОСТ 8.207-76 и МИ 1317-86.

   Характеристики погрешностей измерений разбиты на три группы:

   1 Задаваемые в качестве требуемых или допускаемых — нормы погрешностей измерений.

   2 Приписываемые совокупности измерений, выполняемых по определенной (стандартизованной или аттестованной) методике, — приписанные характеристики погрешностей измерений.

   3 Отражающие близость отдельного, экспериментально полученного результата измерения к истинному значению измеряемой величины статистические оценки характеристик погрешностей измерений.

   Нормы и приписанные характеристики погрешностей измерений применяются при массовых технических измерениях, выполняемых при технологической подготовке производства; в процессах разработки, испытаний, производства, контроля и эксплуатации продукции и т.п. Они представляют собой характеристики генеральной совокупности случайной величины — погрешности измерений.

   Статистические оценки погрешностей измерений применяются при измерениях, выполняемых при проведении научных исследований и метрологических работ. Они представляют собой статистические характеристики случайной величины погрешности измерений.

   К вероятностным характеристикам погрешности измерений относят: с.к.о. погрешности измерений — s(D); с.к.о. систематической составляющей погрешности — s(DS); с.к.о. случайной составляющей погрешности — s().

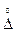   Нижняя и верхняя границы (обозначаются согласно МИ 1317-86 индексами “l” и “h”), в пределах которых находятся погрешности измерений с заданной доверительной вероятностью ().

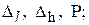
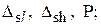
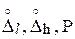   При обозначении характеристик погрешностей в виде норм используется индекс “p”, в виде приписанных погрешностей – индекс “м”, статистические оценки погрешностей отличаются наличием волнистой линии над .

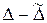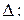
   Основным способом выражения точности измерения согласно ГОСТ 8.207-76 является задание симметричного интервала, в котором с заданной вероятностью Р находится погрешность 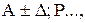где А – результат измерения.

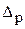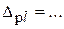   Согласно МИ 1317-86 форма записи результата измерений может, например, иметь следующий вид: А; от до 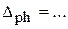; Р=….

   При симметричном интервале 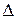результат измерения можно записать в виде А;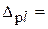 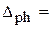…; Р = …

   students-library.com