Второй закон Рауля
Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации (моляльная концентрация, или моляльность, показывает число молей растворенного вещества, содержащихся в 1 кг растворителя моль/кг) раствора и не зависит от природы растворенного вещества. Данный закон справедлив только для бесконечно разбавленных растворов
Для температуры кристаллизации, К называют криоскопической постоянной растворителя и обозначают Kкр
Для температуры кипения, К называют эбулиоскопической постоянной растворителя и обозначают Kэб
Физический смысл криоскопической и эбулиоскопической константы, заключается в понижении температуры кристаллизации и повышения температуры кипения раствора с концентрацией 1 моль/кг.
Второй закон Рауля дает легко осуществимую экспериментально возможность определения молекулярных масс некоторых молекулярных соединений, неспособных к диссоциации в данном растворителе. Действительно, моляльная концентрация растворенного вещества может быть представлена в виде соотношения Cm = gB ∙ 1000 / μB ∙gA, где gA – вес растворителя, gB – вес растворенного вещества, μB – его молекулярная масса. Тогда из ΔT = Kкр · m получим молекулярную массу растворенного вещества:
Пример решения задач на закон Рауля
Вычислите температуру кипения 5%-ного раствора нафталина С10Н8 в бензоле. Температура кипения бензола 80,20 С. Эбулиоскопическая константа его равна 2,57
Из второго закона Рауля
Пусть масса раствора равна 100 грамм, следовательно, масса растворённого вещества равна 5 грамм, а масса растворителя 100 – 5 = 95 грамм.
М (нафталина С10Н8) = 12*10 + 1*8 = 128 г/моль.
Подставляем все данные в формулу и находим повышение температуры кипения раствора по сравнению с чистым растворителем:
ΔT = (2,57*5*1000)/(128*95) = 1,056
Температуру кипения раствора нафталина можно найти по формуле:
www.ximicat.com
Закон Рауля. Криоскопия и эбуллиоскопия;
Третий закон термодинамики.
Расчет абсолютного значения энтропии. Третий закон термодинамики.
Билет №4
Для изолированных систем критерием самопроизвольного течения процесса является рост энтропии.
Энтропия (физический смысл). Каждое макросостояние осуществляется за счет бесчисленного числа микросостояний.
Больцман показал, что чем большее число микросостояний соответствует данному макросостоянию, тем больше термодинамическая вероятность системы, т.е абсолютное значение энтропии является функцией термодинамической вероятности W.
Энтропия – мера молекул состояния, мера хаотичности системы.
Абсолютное значение энтропии всех веществ приводится в справочнике. Для расчета надо:
DS 0 р-ции=ånjDS 0 jпродукты-åniDS 0 iисх.в-в
Энтропия идеального кристалла при 0град. К равна S=0.
Идеальный – кристалл, в котором атомы занимают узлы кристаллической решетки в строгом соответствии с геометрическими законами, т.е. одно возможное микросостояние реализует одно макросостояние.
Энтропия идеального кристалла при 0град.К служит точкой отсчета в шкале энтропии.
Равновесие смещается в том направлении, в котором ослабляется приложенное воздействие, которое уменьшает концентрацию кислорода в воде, за счет его испарения.
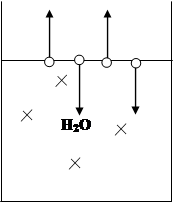(P 0 1-P 0 2)/P1=h2
Рассмотрим чистый растворитель – вод. При определенной температуре на поверхности растворителя наступает момент динамического равновесия, при котором скорость испарения молекул воды равна скорости конденсации. Если в чистый растворитель добавить неэлектролит, то равновесие будет нарушено (концентрация воды в растворе станет меньше). Система отреагирует следующим образом: часть молекул воды из газообразной фазы перейдет в жидкую до тех пор, пока не восстановится равновесие.
Закон Рауля: относительное понижение P 0 1 (давление насыщенного пара раствора над читсым растворителем) прямо пропорционально мольной доле растворенного вещества.
studopedia.su
Коллигативные свойства растворов
Любому раствору характерны те или иные физические свойства, к которым относятся и коллигативные свойства растворов. Это такие свойства, на которые не оказывает влияние природа растворенного вещества, а зависят они исключительно от количества частиц этого растворенного вещества.
К их числу относятся:
- Понижение давление паров
- Повышение температуры кипения
- Понижение температуры затвердевания (кристаллизации)
- Осмотическое давление раствора.
Рассмотрим подробнее каждое из перечисленных свойств.
Понижение давление паров
Давление насыщенного пара (т.е. пара, который пребывает в состоянии равновесия с жидкостью) над чистым растворителем называется давлением или упругостью насыщенного пара чистого растворителя.
Если в некотором растворителе растворить нелетучее вещество, то равновесное давление паров растворителя при этом понижается, т.к. присутствие какого – либо вещества, растворенного в этом растворителе, затрудняет переход частиц растворителя в паровую фазу. Экспериментально доказано, что такое понижение давления паров напрямую зависит от количества растворенного вещества. В 1887 г. Ф.М. Рауль описал количественные закономерности коллигативных свойств растворов.
Первый закон Рауля
Первый закон Рауля заключается в следующем:
Давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально мольной доле растворителя в данном растворе:
p — давление пара над раствором, Па;
p0 — давление пара над чистым растворителем, Па;
χр-ль — мольная доля растворителя.
nв-ва и nр-ля – соответственно количество растворенного вещества и растворителя, моль.
Иногда Первому закону Рауля дают другую формулировку: относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества:
При этом принимаем, что χв-ва + χр-ль = 1
Для растворов электролитов данное уравнение приобретает несколько иной вид, в его состав входит изотонический коэффициент i:
Δp — изменение давления паров раствора по сравнению с чистым растворителем;
i – изотонический коэффициент.
Изотонический коэффициент (или фактор Вант-Гоффа) — это параметр, не имеющий размерности, который характеризует поведение какого – либо вещества в растворе. То есть, изотонический коэффициент показывает, разницу содержания частиц в растворе электролита по сравнению с раствором неэлектролита такой же концентрации. Он тесно связан связан с процессом диссоциации, точнее, со степенью диссоциации и выражается следующим выражением:
n – количество ионов, на которые диссоциирует вещество.
α – степень диссоциации.
Повышение температуры кипения или понижение температуры затвердевания (кристаллизации)
Равновесное давление паров жидкости имеет тенденцию к увеличению с ростом температуры, жидкость начинает кипеть, при уравнивании давления ее паров и внешнего давления. При наличии нелетучего вещества, давление паров раствора снижается, и раствор будет закипать при более высокой температуре, по сравнению с температурой кипения чистого растворителя. Температура замерзания жидкости также определяется той температурой, при которой давления паров жидкой и твердой фаз уравниваются.
Ф.М. Рауль доказал, что повышение температуры кипения, так же как и понижение температуры замерзания разбавленных растворов нелетучих веществ, прямо пропорционально моляльной концентрации раствора и не зависит от природы растворённого вещества. Это правило известно как II закон Рауля:
K — криоскопическая константа,
mв-ва — моляльность вещества в растворе.
Растворы электролитов не подчиняются Законам Рауля. Но для учёта всех несоответствий Вант-Гофф предложил ввести в приведённые уравнения поправку в виде изотонического коэффициента i, учитывающего процесс распада на ионы молекул растворённого вещества:
Осмотическое давление раствора
Некоторые материалы имеют способность к полупроницаемости, т.е. им свойственно пропускать частицы определенного вида и не пропускать частицы другого вида. Так, перемещение молекул растворителя (но не растворенного, в нем вещества), через полупроницаемую мембрану в раствор с большей концентрацией из более разбавленного представляет собой такое явление как осмос.
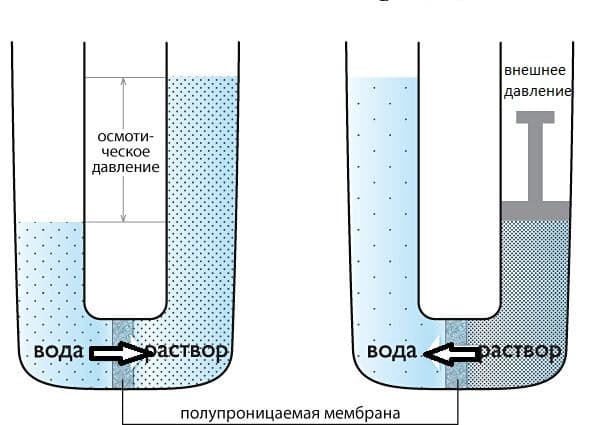ОСМОС
Представим два таких раствора, которые разделены полупроницаемой мембраной, как показано на рисунке выше. Растворы стремятся к выравниванию концентраций, поэтому вода будет проникать в раствор, тем самым уменьшая его концентрацию. Для того, чтобы осмос приостановить, необходимо приложить внешнее давление к раствору. Такое давление, которое требуется приложить, называется осмотическим давлением. Осмотическое давление и концентрацию раствора позволяет связать уравнение Вант — Гоффа, которое напоминает уравнение идеального газа Клапейрона – Менделеева:
где C — молярная концентрация раствора, моль/м 3 ,
R — универсальная газовая постоянная (8,314 Дж/моль·К);
T — абсолютная температура раствора.
Преобразуем уравнение следующим образом:
Для растворов электролитов осмотическое давление определяется уравнением, в которое входит изотонический коэффициент:
где i — изотонический коэффициент раствора.
Для растворов электролитов i > 1, а для растворов неэлектролитов i = 1.
Если полупроницаемой перегородкой разделены два раствора, имеющие одинаковое осмотическое давление, то перемещение растворителя через перегородку отсутствует. Такие растворы называются изотоническими. Раствор, с меньшим осмотическим давлением, по сравнению с более концентрированным раствором, называют гипотоническим, а раствор с большей концентрацией – гипертоническим.
zadachi-po-khimii.ru
Закон Рауля. Расчет характеристик разбавленных растворов по понижению температуры замерзания и по повышению температуры кипения
Для разбавленных растворов закон Рауля формулируется следующим образом: давление насыщенного пара растворителя над раствором (P1) пропорционально мольной доле растворителя в растворе (N1):
(2.6)
где Р1 0 – давление насыщенного пара над чистым растворителем.
(2.7)
В совершенных растворах каждый компонент подчиняется закону Рауля, который в этом случае записывается следующим образом:
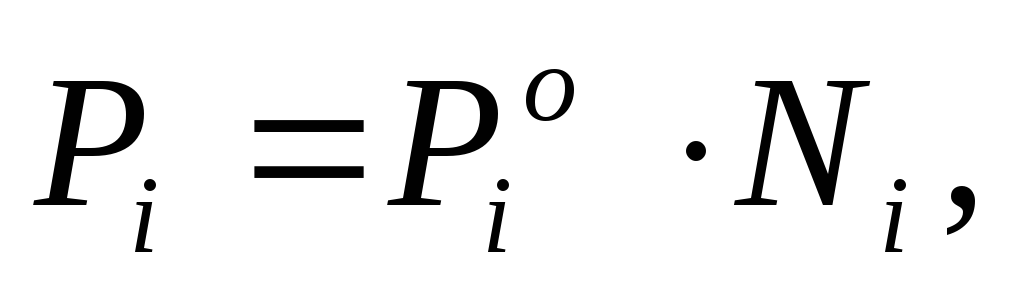(2.7)
где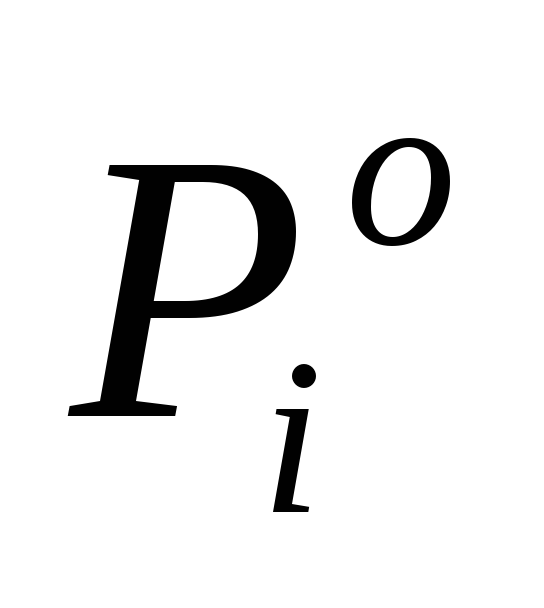 
– давление насыщенного пара над чистым компонентомi.
В этом случае общее давление насыщенного пара над раствором равно сумме парциальных давлений насыщенного пара компонентов раствора:
Уравнение Рауля, учитывающее диссоциацию растворенного вещества в разбавленных растворах, имеет вид:
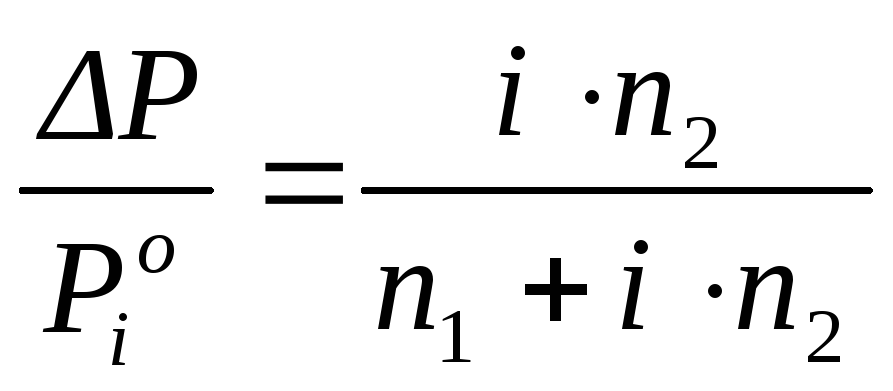, (2.9)
где i – изотонический коэффициент Вант–Гоффа, показывающий, во сколько раз увеличивается число частиц в растворе за счет диссоциации, и связанный со степенью диссоциации α следующим соотношением:
где ν – число частиц, на которые диссоциирует молекула в растворе.
Зависимости повышения температуры кипения (ΔТкип. = Т – Т о кип.) и понижения температуры замерзания (ΔТзам. = Т о зам. – Т) разбавленных растворов от концентрации растворов выражаются следующими уравнениями для недиссоциирующих веществ
и уравнениями для диссоциирующих веществ
Где Токип., Тозам. – температуры кипения и замерзания чистого растворителя;
m – моляльность раствора;
Кэб. и Ккр. – эбулиоскопическая и криоскопическая константы растворителя, зависящие от его природы и не зависящие от природы растворенных веществ. Значения этих констант приводятся в справочной литературе.
По повышению температуры кипения (эбулиоскопический метод исследования – эбулиоскопия) или по понижению температуры замерзания (криоскопический метод исследования –криоскопия) разбавленных растворов можно рассчитывать концентрации растворовm, изотонический коэффициентi, степень диссоциации растворенного веществаαи, учитывая, что моляльность определяется соотношением (2.5), его молярную массуM2:
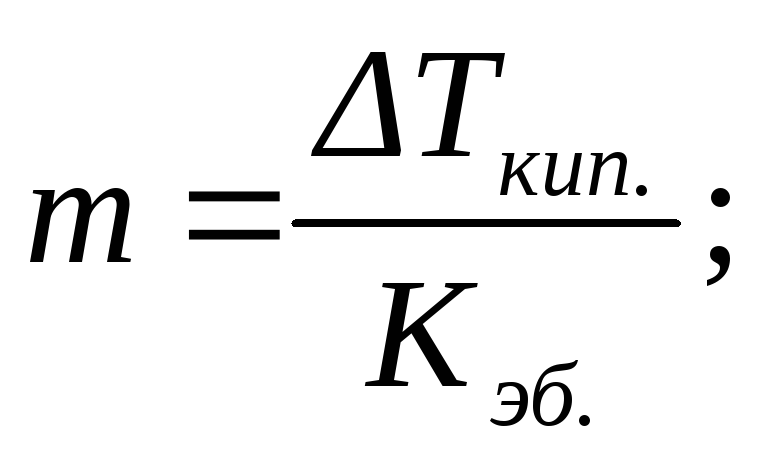или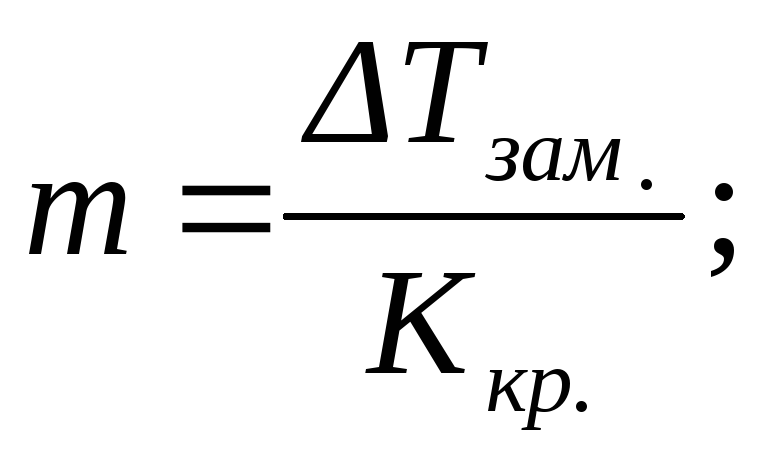 
(2.15)
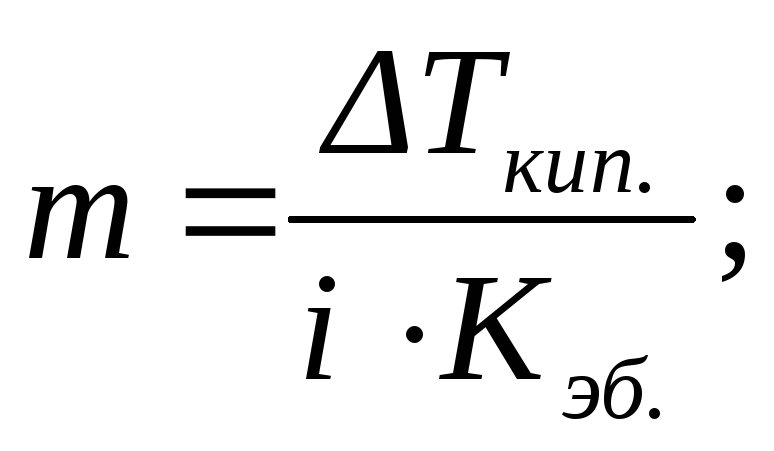или 
(2.16)
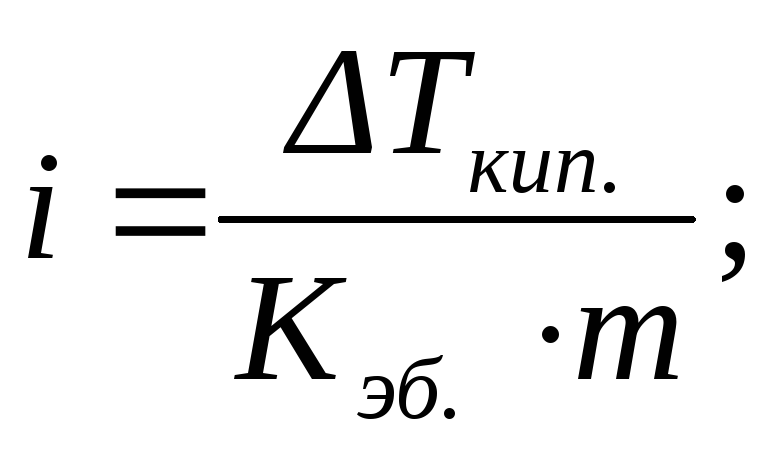или 
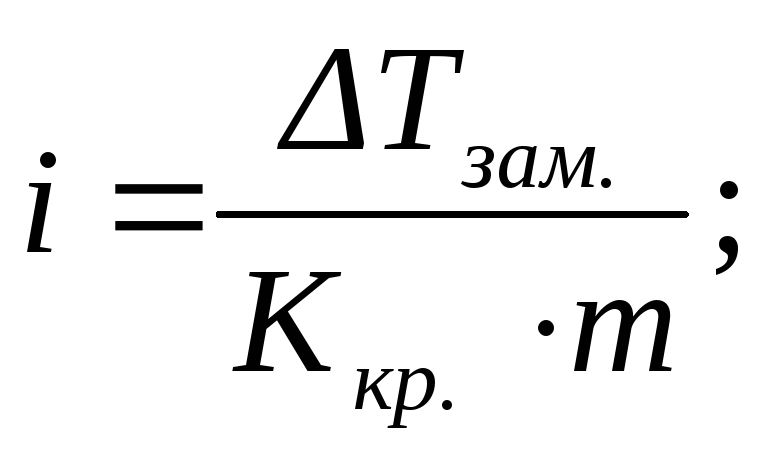(2.17)
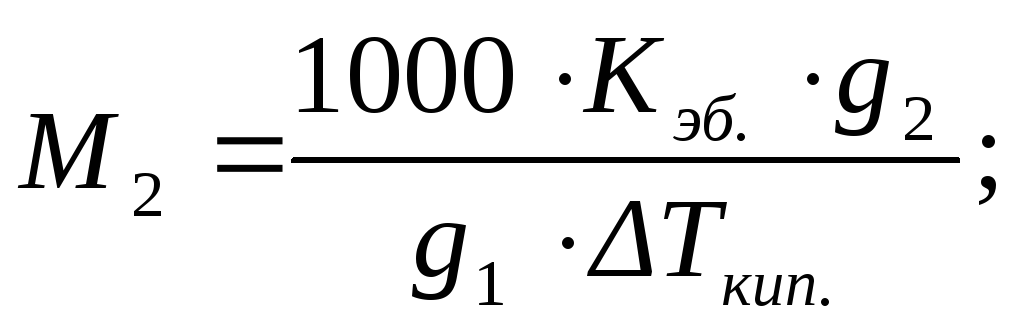или 
(2.18)
П р и м е р 2.2. Давление насыщенного пара воды над раствором нелетучего вещества в воде ниже на 2 % давления пара над чистой водой. Определить моляльность этого раствора. Молярная масса воды М1 = 18 г/моль.
Найдем молярную долю растворенного вещества в данном растворе, для чего воспользуемся уравнением закона Рауля (2.7):
По условию задачи P1 на 2 % ниже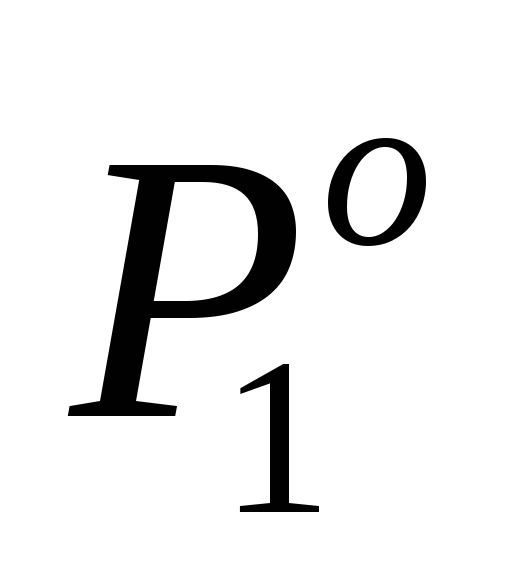
, то есть составляет
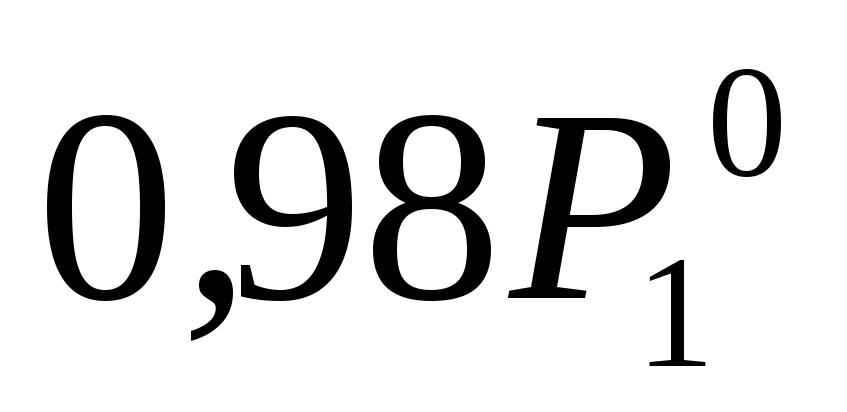, тогда:
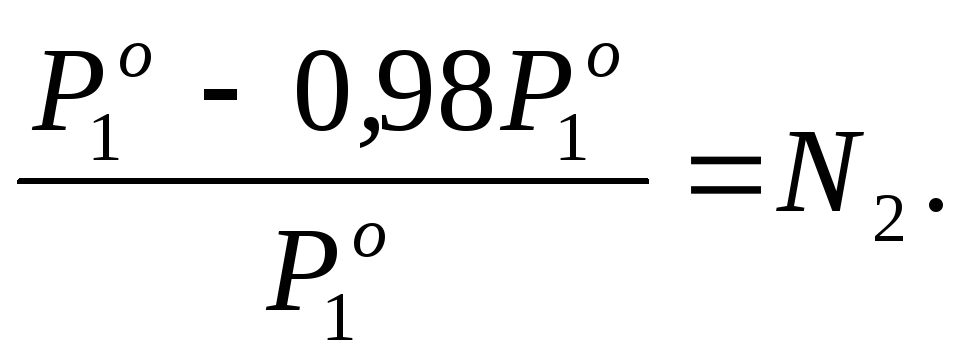
Для определения моляльности mрассчитаем количество молей растворенного веществаn2, приходящееся в растворе на 1000 г воды. В этом случаеm = n2.
Количество молей воды в 1000 г составляет:
В соответствии с определением (2.2) запишем выражение для молярной доли растворенного вещества:
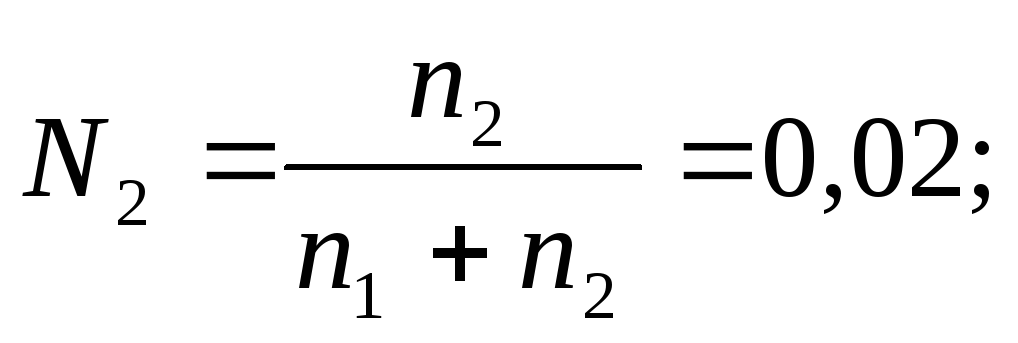
в которое подставим значение n1, а вместо n2 – m, и найдем эту величину:
m = 1,134 моль/1000 г воды.
П р и м е р 2.3. Рассчитать общее давление насыщенного пара над бинарным совершенным раствором при температуре 313 К, состоящим из 200 г дихлорэтана C2H4Cl2 (ДХЭ)и 350 г бензолаC6H6 (Б), если давления насыщенного пара над этими чистыми веществами при указанной температуре составляют:Р о ДХЭ = 2,066·10 4 Па и 
= 2,433·10 4 Па.
Находим количества молей компонентов в растворе:
суммарное количество молей веществ:
Рассчитаем молярные доли каждого компонента в растворе:
Давление насыщенного пара над раствором каждого компонента находится по уравнению закона Рауля для совершенных растворов (2.7):
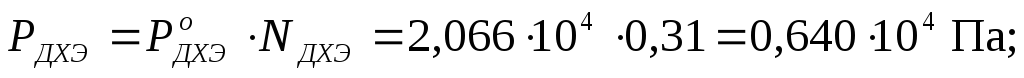
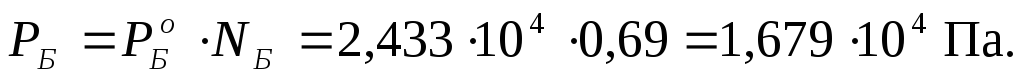
Общее давление рассчитываем по уравнению (2.8):
П р и м е р 2.4. Рассчитать температуру замерзания (кристаллизации) 1 % раствора серы S в железе Fe, если температура кристаллизации чистого железа составляет 1813 К, а его Ккр. = 101,5 К/моль. Молярная масса серы 32 г/моль.
Если данный раствор содержит 1 % растворенного вещества, то в 100 г этого раствора содержится 1 г серы g2 и 99 г железа g1. Рассчитаем моляльность раствора серы в железе по уравнению (2.5):
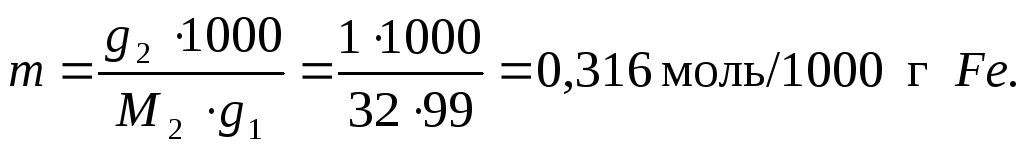
Понижение температуры замерзания рассчитываем по уравнению (2.12):
Температура замерзания раствора серы в железе:
П р и м е р 2.5. Рассчитать, какое количество этиленгликоля C2H4(OH)2 необходимо добавить к 500 г воды g1, чтобы понизить температуру замерзания раствора на 3 градуса. Криоскопическая константа воды Ккр. = 1,86 град/моль. Молярная масса этиленгликоля М2 = 62 г/моль.
Находим моляльность раствора по уравнению (2.15):
Из формулы (2.5) для расчета моляльности:
,
выражаем и рассчитываем величину g2:
П р и м е р 2.6. Вычислить молярную массу вещества, если температура замерзания раствора, содержащего 200 г бензола g1 и 0,4 г исследуемого вещества g2, на 0,17 К ниже температуры замерзания бензола. Криоскопическая константа бензола Ккр. = 5, 16 К/моль.
Расчет производим по формуле (2.18) для криоскопии:
П р и м е р 2.7. Вычислить кажущуюся степень диссоциации соли BaCl2 в 3,2%-ном водном растворе, если температура кипения водного раствора равна 100,21 о С. Молярная масса хлорида бария 208 г/моль. Эбулиоскопическая константа воды Кэб. = 0,512 град/моль.
Определим моляльность раствора по формуле:
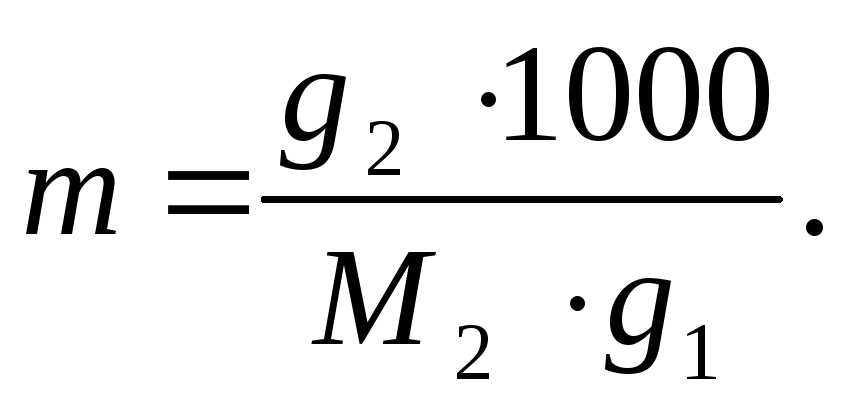
Расчет выполняем для 100г раствора. При указанной массовой концентрации содержание BaCl2 в этом количестве раствора составит 3,2 г g2, а растворителя – воды g1 = 100 – 3,2 = 96,8 г;
моль/1000 г воды.
где 100 о С – температура кипения чистого растворителя (воды).
Находим изотонический коэффициент из уравнения (2.17):
.
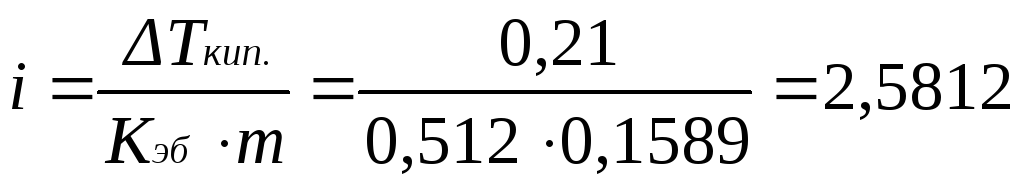Степень диссоциации α находим из соотношения (2.10):
;
для BaCl2 ν = 3, так как при диссоциации одной молекулы этой соли образуются три иона;
.
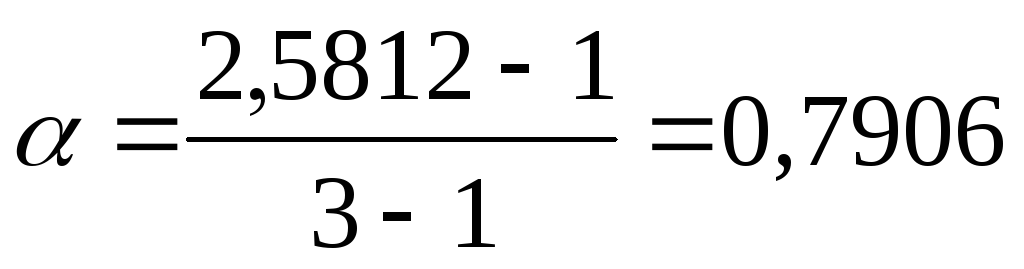Найденная степень диссоциации для сильного электролита является кажущейся, а истинная близка к 1 согласно теории Аррениуса.
studfiles.net
Криоскопия закон рауля
Общим свойством всех жидких систем является давление насыщенного пара жидкости, которое определяется равновесием между жидким и газообразным состоянием вещества. Это равновесие устанавливается на границе раздела фаз жидкость- пар (газ). При растворении в жидкости ( z ) какого-либо нелетучего вещества (х) давление насыщенного пара этой жидкости понижается. Это происходит вследствие того, что концентрация молекул растворителя в поверхностном слое раствора становится меньше чем в чистом растворителе, а значит, равновесие может быть достигнуто при меньшем давлении насыщенного пара. При постоянной температуре величина давления насыщенного пара жидкости зависит от ее летучести и концентрации растворенного вещества. Если обозначить через P ( z ) и Р(у) — давление насыщенного пара растворителя над чистым растворителем и раствором, соответственно, то вышесказанное можно выразить следующими соотношениями:
-разность P ( z ) — P ( y )>0 называется абсолютным понижением давления насыщенного пара растворителя над раствором;
-величина P ( z ) — Р(у) / P ( z ) или D P ( y ) / P ( z ) называется относительным понижением давления насыщенного пара растворителя над раствором.
Первый закон Рауля (1887 г ). Выражает з ависимость относительного понижения давления насыщенного пара растворителя от концентрации раствора неэлектролита. Относительное понижение давления насыщенного пара растворителя над раствором нелетучих веществ равно мольной доле растворенного вещества.
Жидкость закипает, кода давление насыщенного пара этой жидкости становится равным внешнему атмосферному давлению, и кристаллизуется, когда давление насыщенного пара жидкости становится равным давлению насыщенного пара твердой фазы этой жидкости (для воды – лед). Исходя из первого закона Рауля, становится очевидным, что присутствие растворенного вещества понижает температуру кристаллизации раствора и повышает температуру кипения раствора по сравнению с t к p и t кип чистого растворителя.
Второй закон Рауля определяет зависимость температуры кристаллизации и кипения раствора от концентрации растворенного вещества: Повышение температуры кипения и понижение температуры кристаллизации разбавленных идеальных растворов пропорциональны моляльной концентрации растворенного вещества. Δt кип = Ккип·С m , Δt к p = Ккр·С m .
Здесь С m -моляльная концентрация раствора (моль/кг); Ккип — эбуллиоскопическая константа или константа кипения растворителя; Ккр — криоскопическая константа или константа кристаллизации растворителя.
По своему смыслу эбуллиоскопическая и криоскопическая константы показывают повышение температуры кипения и понижение температуры кристаллизации раствора, моляльная концентрация которого равна единице. Используя вышесказанное, можно составить следующие соотношения:
t кип. (у) 0 С = t кип. ( z ) 0 С + Δ t кип , где Δ t кип = t кип( y ) — t кип( z ) .
Например, 1 m водный раствор любого неэлектролита закипает при температуре 100,52°С , а кристаллизуется при температуре –1,86 °С.
Пример 1 . Вычислите осмотическое давление раствора, содержащего в 1,4 л 63 г глюкозы C 6 H 12 O 6 при О°С.
Решение . Согласно закону Вант-Гоффа, Росм = СМ * RT . Сначала рассчитаем молярную концентрацию раствора глюкозы:
V (у) М ( C 6 H 12 O 6 ) · V (у) 180,16 · 1,4
Росм = 0,25 ·8,314 · 273 · 10 3 = 5,67 · 10 5 Па
Пример 2 . Определите температуры кипения и замерзания раствора, содержащего 1 г нитробензола C 6 H 5 NO 2 в 10 г бензола. Температура кипения чистого бензола 80.2 °С, температура кристаллизации -5.4 °С. Ккр = 5,1 °С. Ккип = 2,57 °С .
Решение. Из закона Рауля следует:
где m ( C 6 H 5 NO 2 ) и m (С6Н6) — массы нитробензола и бензола, M ( C 6 H 5 NO 2 ) — молекулярная масса C 6 H 5 NO 2 , которая равна 123,11 г/моль. Подставляя численные значения всех величин в формулы, находим:
Δt к p = [5, l · l ·10 3 ]/ [123,11 · 10] = 4,14 °С,
Δt кип =[2,57 · l ·10 3 ]/ [123,11 · 10] = 2,05 °С.
Находим температуру кипения и кристаллизации раствора:
Криоскопические и эбуллиоскопические константы
24. Найти температуру замерзания и кипения раствора, который содержит 2,4 г неэлектролита (М = 80 г/моль) в 200 г воды.
25. Раствор глюкозы С6Н12 O 6 кристаллизуется при температуре — 0,5 °С. Рассчитайте массу глюкозы, которая приходится на 250 мл воды этого раствора и процентную концентрацию раствора.
26. 25 г неэлектролита (М r = 210 г/моль) растворили в 75 г воды. При какой температуре закипит этот раствор?
27. Давление пара воды над раствором неэлектролита С6Н12 O 6 равно 1707,8 Па при t = 20°С. Рассчитайте массу С6Н12 O 6, содержащегося в 500 г этого раствора, если давление насыщенного пара воды при этой температуре равно 2337,8 Па.
28. Рассчитайте осмотическое давление раствора неэлектролита (М = 180 г/моль) с процентной концентрацией 18% при Т = 290 К. Плотность раствора равна 1,16 г/мл.
29. Сколько граммов воды необходимо взять для растворения 34,2 г сахара С12Н22 O 11, чтобы давление насыщенного пара понизилось на 600 Па при 283 К. При этой температуре давление насыщенного пара воды равно 1227,8 Па.
30. При какой температуре закристаллизуется раствор сахара С12Н22 O 11, если температура кипения его — 100,12 °С . Рассчитайте моляльную концентрацию этого раствора?
31. Водный раствор неэлектролита, содержащий 18,4 г вещества в 200 г воды, кристаллизуется при температуре 0,372 °С. Рассчитайте молекулярную массу растворенного вещества.
32. Сколько граммов неэлектролита (М=186 г/моль) должно содержаться в 1800 г воды, чтобы давление насыщенного пара понизилось на 1000 Па при 283 К. При этой температуре давление насыщенного пара воды равно 1227,8 Па.
33. При одинаковой ли температуре закристаллизуются растворы сахара и глюкозы, содержащие по 24 г в 240 г воды.
4 РАСТВОРЫ ЭЛЕКТРОЛИТОВ
Электролиты — вещества, растворы которых проводят электрический ток. К электролитам относятся кислоты, основания и соли. Электролиты в водных растворах диссоциируют (распадаются) на ионы — катионы (+) и анионы (-). Именно ионы переносят электрический ток в растворах.
Объяснение существования подвижных ионов в растворах электролитов было впервые предложено шведским ученым Аррениусом в 1883 г. Согласно его теории электролитической диссоциации, в растворах электролитов существует равновесие между активной частью электролита, способной проводить электрический ток, и неактивной, не проводящей тока. Теория электролитической диссоциации далее была развита в работах Вант — Гоффа, Менделеева. Диссоциация электролитов происходит при их растворении и является продуктом взаимодействия растворенного вещества и растворителя. К электролитам относятся твердые вещества с ионной кристаллической ионной решеткой (ионная связь), молекулы с полярной ковалентной связью. В общем случае процесс взаимодействия растворенного вещества с растворителем называется сольватацией, а если растворителем является вода, то – гидратацией. Гидратацию можно условно разделить на два составляющих процесса, которые протекают одновременно: разрыв связей в растворяемом веществе (эндотермический процесс) и образование гидратов (экзотермический процесс). Гидраты — это соединения разной прочности между ионами растворенного вещества и полярными молекулами воды. Гидратированные ионы электролита содержат в своем окружении разное число молекул растворителя.
NaCI кр + H 2 O Û NaCI р-р Û Na + * m H 2 O + CI — pH 2 O ,
Твердая фаза раствор гидрат катиона гидрат аниона
где n , p – число молекул растворителя в гидратной оболочке иона. Ч исло молекул растворителя, взаимодействующих с одним ионом, называется числом гидратации. Число гидратации зависит от за
himya.ru