Урок математики в 6-м классе по теме «Сравнение дробей»

Разделы: Математика

Задачи занятия

• Образовательные: научить учащихся сравнивать обыкновенные дроби различными способами
• Развивающие: развивать логическое мышление, познавательные и аналитические способности, учить самостоятельно, добывать новые знания, способствовать развитию правильной математической речи
• Воспитательные: формировать умение работать в коллективе, прислушиваться к мнению сверстников, взаимодействовать со взрослыми.

1 этап (3 минуты)

Приветствие, объявление темы урока.

2 этап (3 минуты)

Как сравнить две обыкновенные дроби с одинаковыми знаменателями? Приведите пример.

Как сравнить две обыкновенные дроби с одинаковыми числителями? Приведите пример.

Как сравнить две обыкновенные дроби с разными знаменателями? Приведите пример.

С какими трудностями мы можем встретиться, сравнивая дроби с разными знаменателями?

Ученики — Иногда бывает трудно подобрать общий знаменатель, встречаются сложные вычисления.

Учитель — Оказывается ребята, наряду с уже хорошо известными нам способами сравнения обыкновенных дробей, существует несколько хитрых приемов, которые помогут нам сравнивать дроби проще и быстрее. Сейчас мы с вами и попробуем догадаться, что это за приемы.

3 этап (15 минут)

Учитель — Представьте частные в виде несократимых дробей:

Ученики — 1/2 2/3 3/4 4/5 5/6

Учитель — Что вы заметили?

Ученики — Числитель дроби на 1 меньше знаменателя.

Учитель — Как вы думаете, в каком порядке расположены дроби?

Ученики — В порядке увеличения.

Учитель — Как доказать?

Ученики — Можно привести к одному знаменателю.

Учитель — Отметьте эти точки на координатном луче, что вы заметили?

Ученики — Чем больше числитель и знаменатель, тем ближе расположено число к 1, т.е. 1/2 отличается от 1 на 1/2, 3/4 отличается от 1 на 1/4, 4/5 отличается от 1 на 1/5

1/2 > 1/3 >1/4 >1/5 > 1/6

Расстояния до 1 сокращаются, значит, сами числа увеличиваются!

Вывод: Обыкновенные дроби можно сравнивать, дополняя их до 1!

Учитель — Используя прием сравнения с 1, сравните: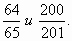

Ученики —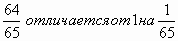

Учитель — Как легче сравнить эти дроби? Приводя к одному знаменателю, или сравнивая с единицей?

Ученики — Конечно, сравнивая с единицей, так как иначе мы столкнемся со сложными вычислениями.

Учитель — Проанализируйте высказывание: если 3 · 7

xn--i1abbnckbmcl9fb.xn--p1ai

Что такое перекрёстное правило

Основные цели: систематизировать и обобщить сведения об обыкновенных и десятичных дробях, научить учащихся пользоваться эквивалентными представлениями чисел в ходе решения задач, обеспечить на этой основе дальнейшее развитие вычислительных навыков и умений решать задачи на проценты, сформировать первоначальные умения статистического анализа больших массивов числовых данных.
Обзор главы. Курс 7 класса начинается с блока арифметических вопросов, своего рода «мостика» между 6 и 7 классами. Здесь еще раз, но уже на новом уровне уделяется внимание взаимосвязи обыкновенных и десятичных дробей, такому важному элементу вычислительной подготовки школьников, как умение сравнивать дроби, совершенствованию навыков выполнения действий с дробными числами. Формирование вычислительных умений продолжается при изучении пункта «Степень с натуральным показателем». Выполняя разнообразные задания с выражениями, содержащими степени, учащиеся одновременно накапливают знания о степенях, которые послужат основой для изучения в последующем свойств степени. В систему упражнений включены задания с буквенными данными; это сделано с целью продолжить обучение числовым подстановкам, вычислению значений буквенных выражений; таким образом, последовательно проводится начатая в 5 классе идея «от чисел к буквам».
В отдельный пункт в данной главе выделено решение задач на проценты. По сравнению с 6 классом, где проценты рассматривались дважды — в связи с изучением обыкновенных и десятичных дробей, здесь предлагаются некоторые новые типы задач; совершенствуется владение такими базовыми техническими приемами, как переход от процентов к дробям и обратно; уделяется внимание умению работать с «большими» процентами, с дробными процентами. Подчеркнем, что этот материал, помимо собственной учебной цели, выполняет еще одну важную функцию: он позволяет продемонстрировать применение математики в быту, в экономике, в социологии и т. д.
Завершается глава пунктом «Статистические характеристики», в котором продолжается начатое в 5—6 классах изучение описательной статистики. Учащиеся знакомятся с такими понятиями описательной статистики, как среднее арифметическое, мода, размах, и приобретают первоначальные умения по их применению для анализа массивов числовых данных.
Начиная с этой главы при решении задач предполагается регулярное использование калькулятора для выполнения громоздких вычислений. Здесь он применяется для нахождения приближенных десятичных значений обыкновенных дробей с большими знаменателями, для вычисления степеней с большими показателями, для получения ответа при решении некоторых задач на проценты, для вычисления статистических характеристик больших массивов числовых данных. Калькулятор позволяет обогатить систему упражнений, включить в нее экспериментальную работу с числами, задания с реальными числовыми данными, что важно с точки зрения усиления прикладного аспекта обучения, его практической ориентации. Но при этом его использование ни в коем случае не отменяет «ручные» вычисления. Наоборот, навыки оценки и прикидки результата, эффективные вычислительные приемы остаются весьма актуальными.
В качестве необязательного материала в пункте «Для тех, кому интересно» предлагается небольшой фрагмент, посвященный исследованию последней цифры степени. В ходе выполнения упражнений учащимся придется экспериментировать с числами, подмечать закономерности, проводить несложные доказательные рассуждения.

1.1. Сравнение дробей

Комментарий к упражнениям

20. Каждый раз обсуждается вопрос о том, какая форма представления дробей будет использоваться. Перед выполнением заданий «д» — «з» нужно вспомнить правила действий с отрицательными числами на простых примерах с целыми данными (особенно это важно в слабом классе).
21. Рекомендуем в каждом случае сопоставить примеры и обсудить порядок выполнения действий.
23. Запись выражения с помощью дробной черты — трудный момент. Важно, чтобы при переходе к записи в виде дроби не менялся порядок действий. Можно восстановить скобки как группирующий символ.
б) ( 2,4 : 1,08 ) ⋅ 0,15 = 2,4 1,08 ⋅ 0,15 = 2,4 ⋅ 0,15 1,08 = . .
24. Каждый знак деления надо заменить дробной чертой.
в) ( 0,324 : 1,08 ) : 0,033 = 0,324 1,08 : 0,033 = = 0,324 ⋅ 100 000 1,08 ⋅ 0,033 ⋅ 100 000 = 32 400 108 ⋅ 33 = 100 11 = 9 1 11 .
29. Можно сначала показать, что в каждом случае берется число, противоположное числу, заключенному в скобках. Например, −(x + y) — это число, противоположное сумме x + y. Поэтому возможно такое решение:

1.3. Степень с натуральным показателем

Изучение степени с натуральным показателем в 7 классе осуществляется в два этапа. Основная цель данного пункта — накопление знаний о степенях на основе практического опыта, создание своего рода основы для последующей формализации (см. гл. 6).
Из курса математики 5—6 классов учащиеся знают, что означают такие числовые выражения, как, например, 6 3 , (−0,5) 4 , есть у них и некоторый опыт вычисления степеней. В результате изучения данного пункта они должны твердо знать обозначение степени в общем виде и соответствующую терминологию, использовать степени в записи разложения чисел на простые множители, в представлении числа в виде суммы разрядных слагаемых. Кроме того, они должны познакомиться с записью больших и малых чисел с помощью степени числа 10. Наконец, учащиеся должны научиться находить значения степеней с отрицательными основаниями, а также знать, как зависит знак степени с отрицательным основанием от того, четным или нечетным числом является показатель степени.
Подчеркнем, что все упражнения к пункту выполняются лишь на основе знания того, что выражение а n , где n — натуральное число, большее 1, означает произведение n множителей, равных а. Никакими формальными правилами действий со степенями учащиеся пока не владеют, и такие упражнения, как, например, 45 и 46, они должны выполнять по смыслу, опираясь только на указанное определение.
Упражнения раздела А весьма разнообразны и позволяют рассмотреть все основные аспекты изучаемого вопроса. В классах с невысоким уровнем подготовки рекомендуем ограничиться упражнениями раздела А (возможно, кроме упражнений 45, 48, 51, 52, 53, 60).

Комментарий к упражнениям

43. Представить степень в виде произведения степеней с одинаковыми основаниями можно разными способами. Например, 5 7 = 5 2 · 5 5 или 5 7 = 5 3 · 5 4 , 5 10 = 5 5 · 5 5 или 5 10 = 5 2 · 5 3 · 5 5 .
44. г) 729 = 3 · 3 · 3 · 3 · 3 · 3 = 3 6 ,
729 = (3 · 3) · (3 · 3) · (3 · 3) = 9 3 ,
729 = (3 · 3 · 3) · (3 · 3 · 3) = 27 2 .
45. Полезно (но необязательно) вспомнить комбинаторику и указать все возможные варианты такого представления для п. «а». В пп. «б» и «в» сделать это труднее, и такая постановка вопроса возможна только для сильных учащихся.
а) Возможны такие варианты: 3 1 · 3 7 = 3 2 · 3 6 = 3 3 · 3 5 = 3 4 · 3 4 .
б) Переберем все варианты. Для этого поступим следующим образом: «зафиксируем» один из показателей и переберем все возможные варианты двух других. Получим пять вариантов:

1.4. Задачи на проценты

Комментарий к упражнениям

в) Рассуждая аналогично, представим условие в виде рисунка (рис. 2, а). Чтобы узнать, какую часть стоимости чашки составляет стоимость блюдца, цену чашки примем за 100% (рис. 2, б). Тогда из рисунка видно, что стоимость блюдца составляет 5 6 стоимости чашки, или в процентах:
5 6 ⋅ 100 % = 83 1 3 % .

1.5. Статистические характеристики

Методический комментарий

В этом пункте продолжается знакомство учащихся с описательной статистикой, начатое в 5 и 6 классах, где рассматривались наглядные способы представления информации — таблицы и диаграммы. Основная цель данного пункта — формирование первоначальных представлений о статистическом анализе ряда данных. Учащиеся знакомятся с такими простейшими статистическими характеристиками, как среднее арифметическое, мода и размах. Разнообразные по сюжетам упражнения позволят учащимся не только поупражняться в нахождении этих характеристик, но и увидеть сферу их практического применения, различные содержательные интерпретации. Так, средний рост солдата — это среднее арифметическое приведенного ряда (см. упражнение 97); размер обуви, пользующийся наибольшим спросом, — это мода ряда размеров (см. упражнение 98); средний балл спортсмена — это среднее арифметическое выставленных оценок (см. упражнение 101).
Все упражнения к пункту в принципе не являются трудными (кроме упражнения 109 — задачи-исследования). Но нужно иметь в виду, что при выполнении заданий раздела Б следует пользоваться вторым способом вычисления среднего арифметического, разобранным в тексте учебника.
В классах с невысоким уровнем подготовки рекомендуем, кроме задач раздела А, разобрать еще, например, упражнения 103 и 108. В ходе классной работы целесообразно выполнить упражнения 94 (а), 95, 96 (а, б), 97, 100, 102, 103, 105, 107, 108. Для работы дома: упражнения 98, 99, 101, 104, 106.

103—105. В задачах при нахождении среднего арифметического нужно сумму одинаковых слагаемых заменять соответствующим произведением, как это показано в объяснительном тексте учебника.
104. Мода равна 4, так как оценку «4» получили 12 человек (наибольшее количество). Средний результат по контрольной работе находим, разделив общую сумму баллов на количество учеников, писавших работу.
107. б) Указание . Умножьте среднее арифметическое на 1200.
108. Он, скорее всего, вычислил для каждой группы сотрудников среднее арифметическое пропущенных дней. В первом случае это ≈ 3,7 дня, а во втором — ≈ 1,65 дня.
109. 2) Выводы делаются на основе наблюдений при выполнении первого задания.
а) Среднее арифметическое и мода ряда увеличатся на это же число, размах не изменится.
б) Среднее арифметическое, мода ряда и размах изменятся во столько же раз.

1.6. Последняя цифра степени
(Для тех, кому интересно)

В этом пункте представлен материал, который может оказаться вполне посильным и интересным для многих учащихся. Интерес может вызвать уже то, что, оказывается, совсем нетрудно узнать, какой цифрой оканчивается такое огромное число, как, например, 2 100 . Для этого нужно немного поэкспериментировать и подметить закономерность, по которой меняется последняя цифра степени с основанием 2.
Из опорных умений, необходимых для выполнения упражнений к данному пункту, помимо умения возводить последовательно число в натуральную степень, нужно еще уметь выполнять деление с остатком.

110. Будем последовательно возводить в степень число 3 и наблюдать, как меняется последняя цифра:
3 1 = 3, 3 2 = 9, 3 3 = 27, 3 4 = 81, 3 5 = 243 и т. д.
Таким образом, степени числа 3 могут оканчиваться цифрами 3, 9, 7 и 1, которые повторяются через четыре шага.
Так как 10 = 4 · 2 + 2, то степень числа 3 10 оканчивается такой же цифрой, что и число 3 2 , т. е. цифрой 9. Так как 15 = 4 · 3 + 3, то степень числа 3 15 оканчивается цифрой 7; так как 120 кратно 4, то степень числа 3 120 оканчивается цифрой 1; так как 126 = 4 · 32 + 2, то степень числа 3 126 оканчивается цифрой 9.
111. Имеем 7 1 = 7, 7 2 = 49, 7 3 = 343, 7 4 = 2401, 7 5 = 16 807, т. е. через четыре шага последние цифры повторяются. Таким образом, степени числа 7 оканчиваются цифрами 7, 9, 3, 1.
112. При делении показателя 10 на 4 в остатке получается число 2. Такой же остаток получается при делении на 4 показателя 102. Значит, числа 2 10 и 2 102 оканчиваются одной и той же цифрой.
113. Указание . Докажите, что при делении чисел 33, 333 и 3333 на 4 получается один и тот же остаток.
114. Это числа 5 и 6, а также любые числа, оканчивающиеся цифрами 0, 1, 5, 6.
115. Числа 4 m и 4 n оканчиваются одной и той же цифрой, если числа m и n оба четные или оба нечетные.
116. Сумма 11 14 · 3 22 делится на 10, так как слагаемое 11 14 оканчивается цифрой 1, слагаемое 3 22 — цифрой 9, а их сумма — цифрой 0. Разность 7 20 − 9 10 делится на 10, так как уменьшаемое 7 20 оканчивается цифрой 1, вычитаемое 9 10 — также цифрой 1, а значит, разность — цифрой 0. Произведение 12 15 · 15 12 содержит множители 2 и 5, а следовательно, делится на 10.

Дополнительные задания к главе 1

Указания и решения

Упростив его, получим x + 83 = 98. Найдем неизвестное число: x = 15.
142. а) Сумма десяти чисел равна 50. Если к ряду этих чисел приписать число 16, то сумма будет равна 66, а чисел станет 11. Найдем среднее арифметическое: 66 11 = 6 .
б) Среднее арифметическое равно частному 32 − 11 7 = 3 .
143. Среднее арифметическое равно частному

old.prosv.ru

Консультация для преподавателей 5 класса (январь)

Тема консультации: «ДРОБИ»

Дидактическая основа

Дидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000. ». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивают личностные и метапредметные результаты образования, соответствующие ФГОС.

Содержание консультации

В соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 5 класса в январе продолжается работа с третьей главой «Дроби». Изучаются § 1. «Понятие дроби» (П.3.1.2 «Основное свойство дроби. Преобразование дробей»; П.3.1.3 «Сравнение дробей») и § 2. «Арифметика дробей» (П.3.2.1 «Сложение и вычитание дробей»), содержание которых продолжает развитие числовой содержательно-методической линии курса.

Вместе с тем, в процессе изучения этих пунктов параллельно развиваются и все остальные линии курса. Такой подход является общим для данного курса: на каждом этапе его изучения, параллельно с ведущей линией, по которой идет расширение понятийной базы, закрепляются и отрабатываются знания и умения по всем остальным разделам курса.

Основные содержательные цели:

• вывести основное свойство дроби, сформировать умение сокращать дроби, приводить дроби к новому знаменателю и числителю;
• сформировать умение сравнивать дроби с помощью приведения дробей к одинаковому числителю, знаменателю, промежуточного числа, дополнения дроби до 1, «перекрёстного» правила;
• сформировать умение складывать и вычитать дроби (общий случай).

Тематическое планирование

В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по учебнику 5 класса возможно в условиях различных учебных планов образовательных учреждений. Поэтому тематическое планирование по изучению данного курса разработано для 5 ч и для 6 ч в неделю. При 6 ч в неделю добавочные часы идут на выполнение дополнительных заданий и уроки рефлексии, позволяющие учащимся лучше усвоить изучаемый материал.

Тематическое планирование разработано в двух вариантах: для учителей, закончивших ознакомительные курсы по программе «Школа 2000. » и работающих на базовом (содержательном) уровне реализации дидактической системы «Школа 2000. », и для учителей, закончивших углубленные курсы по программе «Школа 2000. » и работающих на технологическом уровне реализации дидактической системы «Школа 2000. ».

Мы предлагаем Вам скачать тематическое планирование на III четверть (5 ч в неделю).

Методические рекомендации к организации учебного процесса

§ 1. Натуральные числа и дроби. П.2 Основное свойство дроби. Преобразование дробей

1) В результате изучения пункта 3.1.1 учащиеся повторили известные им из курса начальной школы сведения о дробях. Среди них были зафиксированы правила, которые будут уточняться для общего случая в ходе изучения третьей главы: правила сравнения дробей с одинаковыми числителями, знаменателями, правило сложения и вычитания дробей с одинаковыми знаменателями. В связи с этим учащиеся знакомятся с основным свойством дроби в пункте 3.1.2 «Основное свойство дроби. Преобразование дробей».

2) Для открытия основного свойства дроби можно использовать дополнительные свойства умножения и деления (делимое и делитель можно умножать и делить на одно и то же натуральное число) и знание, что результат деления можно записать в виде дроби, а также умение изображать дроби на числовом луче.

3) Учащиеся учатся применять основное свойство дроби для преобразования дробей – сокращение дроби и приведения дроби к новому числителю (знаменателю). После знакомства учащихся с таким преобразованием дроби, как сокращение дроби, вводится понятие несократимой дроби.

4) Для сокращения дробей предлагается использовать три способа: сокращать дробь на НОД числителя и знаменателя, сокращать дробь последовательно на общие делители (с использованием признаков делимости) или представлять числитель и знаменатель в виде произведения.

5) При выполнении системы заданий №№ 66, 67 (б), 86 – 88 идет последовательная работа по построению алгоритма приведения дробей к наименьшему общему знаменателю (при этом сначала формируется представление о новом знаменателе, как о числе кратном старому знаменателю, затем вводится понятие дополнительных множителей, после чего, при выполнении № 87, вводится понятие общего знаменателя двух дробей и формируется понятие общего знаменателя как общего кратного знаменателей). И только после такой подготовительной работы ставится проблема приведения дробей к наименьшему общему знаменателю. При выполнении №№ 88 – 89 формируется умение применять полученный алгоритм.

6) Аналогичная работа может быть проведена для построения алгоритма приведения дробей к новому числителю.

7) В третьей главе пятиклассникам предлагаются задания, содержащие алгебраические дроби. Так, при отработке умения преобразовывать дроби учащимся могут быть предложены задания сократить алгебраическую дробь, числитель которой имеет вид многочлена (№№ 83 (1, 2, 3), 92). При выполнении заданий такого уровня учителю следует реализовывать принцип минимакса: работать на уроке, ориентируясь на сильных учеников на высоком уровне сложности, оценивая при этом только успех, а контролировать усвоение материала каждым учащимся на уровне минимума, определенного в стандарте.

§ 1. Натуральные числа и дроби. П.3 Сравнение дробей

8) В третьем пункте «Сравнение дробей» учащиеся строят разные способы сравнения дробей: приведение дробей к наименьшему общему знаменателю и к наименьшему общему числителю (№№ 135 – 142). В данном пункте рассматриваются и «хитрые приемы», которые в некоторых случаях удобнее использовать для сравнения дробей: это способ сравнения дробей с единицей (неправильная дробь больше правильной), с промежуточным числом (с половиной), метод дополнения дроби до 1 («ближе к единице»), «перекрёстное» правило.

9) Для отработки приема сравнения с промежуточным числом (1/2) выполняется № 145. При этом учитель может использовать такие модели, как числовой луч или отрезок. После сравнения данных чисел с половиной на моделях учитель может задать вопросы о сравнении пар дробей, одна из которых больше половины, а другая – меньше. Учащимися делается вывод об использовании промежуточного числа для сравнения дробей. Например, можно записать, что 41/80 > 245/504, потому что первая дробь больше половины, а вторая – меньше.

10) Для знакомства учащихся с приемом сравнения правильных дробей путем определения, какая из них «ближе к единице», а значит, и больше (№ 143), можно поступить следующим образом: учащимся предлагается проанализировать данные дроби. Учащиеся должны заметить, что числитель отличается от знаменателя на 1, после чего можно задать вопрос, к какому числу близки данные дроби. Затем учитель предлагает изобразить первую пару дробей и единицу на числовом луче и показать, сколько «не хватает» дроби 8/9 до целого и сколько «не хватает» 15/16, то есть выяснить, какие дроби дополнят данные до единицы. Учащиеся фиксируют, что дополнения составляют в первом случае девятую часть, а во втором – шестнадцатую часть единичного отрезка. Делается вывод: дробь с большим знаменателем «ближе» к единице, а значит, больше. Следующие пары дробей сравниваются уже без числового луча (№ 144).

11) Также учащиеся узнают общее правило сравнения дробей – «перекрёстное» правило ( a/b ad ad = bc , с которым нужно познакомить учащихся. Необходимо заострить внимание учащихся на этом утверждении, так как данное условие позволит им решать уравнения нового вида, а в дальнейшем будет использоваться в 6 классе при изучении тем «Отношение» и «Пропорция». Условие равенства дробей применяется при выполнении № 151.

12) После изучения правил сравнения обыкновенных дробей учащиеся получают возможность построить правила сравнения любых смешанных чисел. Для формирования умения применять правила сравнения смешанных чисел учащимся предлагается выполнить № 147 (7, 8).

13) Таким образом, пятиклассники могут выполнить сравнение дробей следующими способами: приведение дробей к наименьшему общему знаменателю, наименьшему общему числителю, пользуясь свойством «любая неправильная дробь больше правильной», сравнение с промежуточным числом (с 1/2), метод «ближе к 1» и универсальный способ – общее правило сравнения дробей. Использование различных способов для сравнения дробей реализует принцип вариативности ДСДМ, который предполагает формирование у учащихся способностей к систематическому перебору вариантов и адекватному принятию решений в ситуациях выбора (№ 147).

14) Способы сравнения дробей используются учащимися для решения задач (№ 153, № 154).

15) При обсуждении № 155 появляется возможность формировать не только предметные, но и личностные результаты обучения, которые соответствуют новым целям образования. В заданиях учебника математики курса «Учусь учиться» заложены представления о дружбе, доброте, чести, трудолюбии и других ценностных качествах человека, которые опосредованно оказывают эмоциональное воздействие на детей и способствуют выработке морально-этических норм и правил. При выполнении данного задания у учителя появляется возможность выслушать мнения учащихся и подвести их к собственным выводам о самооценке человека.

§ 2. Арифметика дробей. П.1 Сложение и вычитание дробей

16) В начальной школе учащиеся научились складывать и вычитать дроби с одинаковыми знаменателями. В пункте «Сложение и вычитание дробей» они учатся находить значение суммы и разности любых дробей.

17) Перед выполнением пробного задания можно предложить учащимся проанализировать данную сумму 2/21 + 6/35. Пятиклассники фиксируют, что слагаемыми являются дроби с разными знаменателями. При выполнении задания ученики фиксируют затруднение: «не можем найти сумму» или «не можем обосновать своё решение». Причиной затруднения является отсутствие правила сложения дробей с разными знаменателями. В результате работы учащиеся строят алгоритм сложения и вычитания любых дробей:

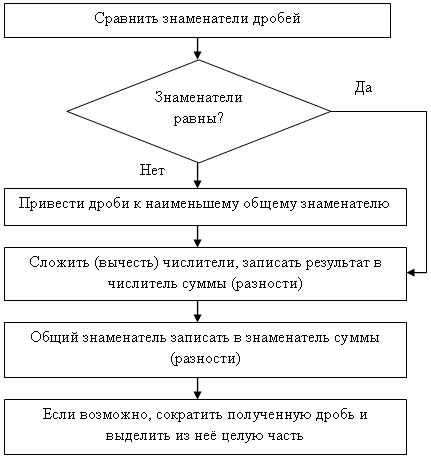
18) На последующих уроках учащиеся применяют алгоритм сложения и вычитания обыкновенных дробей для решения уравнений, нахождения значения буквенных выражений при заданном значении букв, решения задач.

19) Для обыкновенных дробей фиксируются и применяются переместительное и сочетательное свойства сложения и правила вычитания суммы из числа и числа из суммы. (№№ 201 – 202).

20) В результате изучения данных тем у учащихся появляются следующие эталоны: основное свойство дроби, алгоритм приведения дробей к наименьшему общему знаменателю (числителю), несколько способов сокращения дробей, понятие несократимой дроби, правила сравнения дробей, алгоритмы сложения и вычитания дробей (общий случай). Данные эталоны приведены в учебном пособии Л.Г. Петерсон, Л.А. Грушевской «Построй свою математику», которое предусматривает специальную работу с ними.

Приведем пример эталона из указанного пособия:

Методические рекомендации по планированию уроков

При организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствии с зоной ближайшего развития более подготовленных учащихся. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.

Мы предлагаем Вам скачать методические рекомендации по планированию уроков.

С примерами организации уроков по изучению темы «Дроби» Вы можете познакомиться в серии дисков со сценариями уроков в технологии деятельностного метода к учебнику математики для 5 − 6 классов основной школы авторов Г.В. Дорофеева, Л.Г. Петерсон по программе «Учусь учиться».

Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000. ».

Тема: «Сокращение дробей»

Автор: Л.А. Грушевская

1) cформировать понятия сократимой и несократимой дроби, умение сокращать дроби на основе использования основного свойства дроби;

2) повторить и закрепить понятия делителя и кратного, признаки делимости, свойства делимости произведения, чтение и нахождение значений буквенных выражений, тренировать умение строить математические модели текстовых задач.

Мы предлагаем Вам cкачать сценарий урока

(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как. «)

Уважаемые коллеги! В соответствии с Вашими просьбами предлагаем Вам скачать решение задач на смекалку, которые входят в данные параграфы.

Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.

www.sch2000.ru