Частица совершает гармонические колебания. Найти координату и скорость частицы — Колебания и волны

Точка совершает гармонические колебания. Найти круговую частоту колебаний.
Точка совершает гармонические колебания. Максимальная скорость точки .

Маленький шарик совершает гармонические колебания по двум гладким плоскостям
Маленький шарик совершает гармонические колебания с частотой v без трения вниз.

Найти циклическую частоту, амплитуду и начальную фазу результирующего колебания частицы
1)Частицы одновременно учавствуют в двух колебаниях одного направления.

Гармонические колебания
Точка совершает гармонические колебания по закону х = А.cos(wt +φ), где А = 4.

Innocent77, если не сходится, то бывает, именно из-за неправильного решения.
Не стесняйтесь показывать решение и говорить пожалуйста в обращении. Иначе в это всё невозможно поверить.

Теперь из пары этих же уравнений для t=П/8 удастся найти A и потом подставьте в формулы синусоиды и косинусоиды время t=П/8+ 2,4 с и будет вам счастье.

Гармонические колебания
На движущейся со скоростью V тележке,находится груз,при крепленный к ней.

Гармонические колебания
Доброго времени суток. Может кто-то объяснить гармонические колебания? (решение.

Гармонические колебания
Помогите решить задачу точка совершает гармонические которые колебания.

Гармонические колебания
Пожалуйста, помогите решить. Груз массой m = 20 г c совершает гармонические.

www.cyberforum.ru

Механические и электромагнитные колебания

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

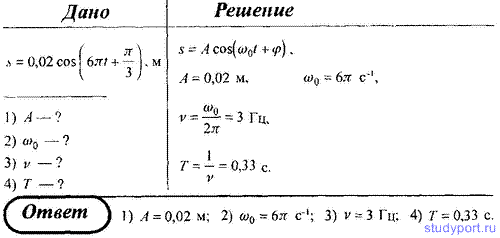
2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

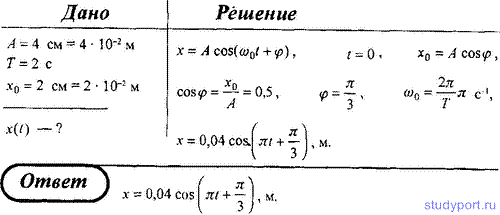
4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

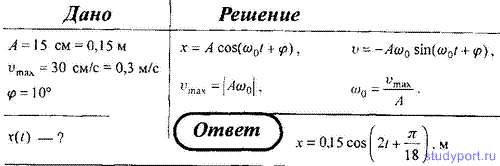
6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

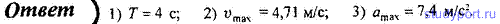
7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

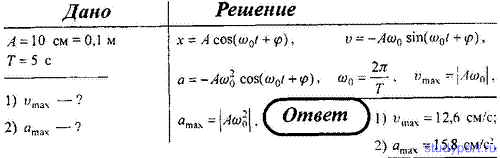
8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

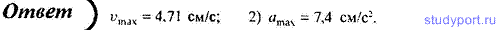
12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

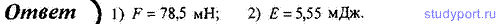
15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

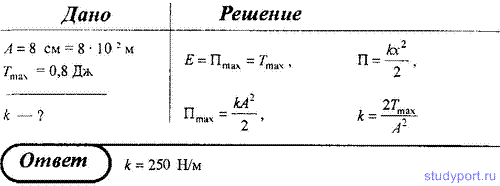
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

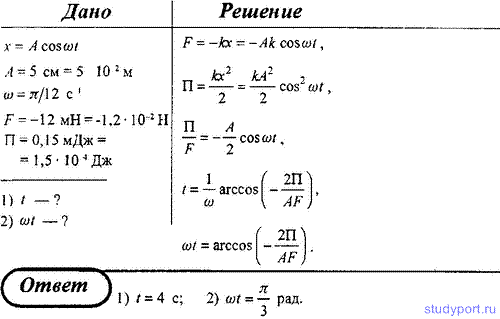
20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с -1 . Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

studyport.ru

Примеры решения задач. ЗАДАЧА 1.Частица совершает гармонические колебания вдоль оси ОХ около положения равновесия х = 0

ЗАДАЧА 1.Частица совершает гармонические колебания вдоль оси ОХ около положения равновесия х = 0. Частота колебаний 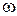= 4,00с –1 . В некоторый момент времени координата частицы х₀= 25,0 см и ее скорость
u₀ = 100 cм/c. Найти координату х и скорость частицы u через время t = 2,4 с после этого момента.

АНАЛИЗ. Для решения воспользуемся уравнениями кинематики гармонических колебаний.

РЕШЕНИЕ. Закон движения частицы, совершающей гармонические колебания, определяется уравнением (1.1.1):

. (1.1.6)

За начало отсчета времени (t = 0) выберем момент, для которого заданы начальные условия: х₀ = 25,0 см = 0,250 м,u₀= 100 см/с = 1,00 м/с, колеблющейся частицы.

Закон изменения скорости со временем найдем, продифференцировав по времени уравнение (1.1.6):

. (1.1.7)

Уравнения (1.1.6) и (1.1.7) в точке t = 0 с учетом начальных условий имеют вид:

x₀= Acos 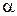, u₀= – A 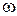sin .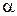

Получили систему из двух уравнений для определения амплитуды А и начальной фазы 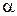. Из них найдем:

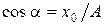, (1.1.8)

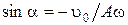. (1.1.9)

Уравнения (1.1.8) и (1.1.9) почленно возведем в квадрат и сложим:

.

Амплитуда колебаний А равна:

м.

Правильность формулы по размерности очевидна.

Разделив выражения (1.1.9) на (1.1.8), найдем тангенс начальной фазы колебаний:

.

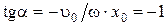Учитывая, что ,определим начальную фазу :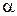

a = 180° – 45° = 135° = 3p/4 = 2,35 рад.

Подставив численные значения А и 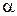в уравнения (1.1.6) и (1.1.7), получим:

, м; 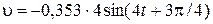, м/с.

Найдем искомые значения координаты x₁и скорости 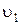в момент времени t₁= 2,40 c:

ЗАДАЧА 2. Колебательный контур (рис. 1.1.5) состоит из конденсатора емкостью С = 0,025мкФ и катушки с индуктивностью L = 1,015Гн. Омическим сопротивлением цепи следует пренебречь. Конденсатор заряжен количеством электричества q₀= 2,5×10 –6 Кл. Написать для данного контура уравнения изменения: 1) разности потенциалов U_C на обкладках конденсатора , 2) падения напряжения U_L на катушке индуктивности, 3) силы тока в цепи в зависимости от времени. Найти сдвиг по фазе между напряжением U_С на обкладках конденсатора и: а) током I в цепи, б) напряжением U_L на катушке индуктивности. Найти уравнение фазовой траектории осциллятора.

АНАЛИЗ. В задаче рассматриваются незатухающие колебания в электрическом колебательном LC контуре при отсутствии омического сопротивления. с частотой .

РЕШЕНИЕ. Заряд на обкладках конденсатора изменяется по закону (1.1.1):

. (1.1.10)

Сила тока в контуре

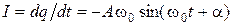. (1.1.11)

Напряжение на катушке индуктивности найдем, используя закон Фарадея и равенство (1.1.11):

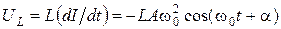. (1.1.12)

Напряжение на обкладках конденсатора с учетом равенства (1.1.10) имеет вид:

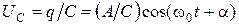. (1.1.13)

Сравнение выражений для заряда (1.1.10) и напряжения U_C (1.1.13) показывает, что эти величины изменяются в одной фазе.

Закон изменения силы тока (1.1.11) можно представить в виде

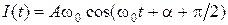. (1.1.14)

Ток I в контуре опережает по фазе на напряжение U_C на обкладках конденсатора. Закон изменения напряжения U_L на катушке индуктивности получим из уравнения (1.1.12):

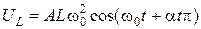. (1.1.15)

Сравнение уравнения (1.1.13) с (1.1.15) показывает, что напряжение на катушке индуктивности опережает по фазе на 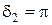напряжение на обкладках конденсатора.

Определим численные коэффициенты в уравнениях (1.1.10), (1.1.13), (1.1.14), (1.1.15). Будем считать, что при t = 0заряд на обкладках конденсатора достигает максимального значения: q = A = q₀ , тогда из равенства (1.1.10) получим 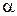= 0. Закон изменения заряда имеет вид: q = q₀сos t, где 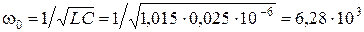рад/c.

Закон изменения разности потенциалов U_C на обкладках конденсатора (1.1.13) с числовыми коэффициентами:

, В.

Закон изменения со временем силы тока I c числовыми коэффициентами получим из уравнения (1.1.14):

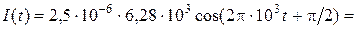
, A.

Закон изменения напряжения U_L на катушке индуктивности получим из уравнения (1.1.15):

U_L = 2,5×10 –6 ×1,015×6,28 2 ×10 6 cos(2 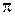×10 3 t+ 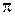) = 100cos(2 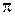×10 3 t+ 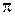),В.

Напряжения U_С на обкладках конденсатора и U_L на катушке индуктивности изменяются в противофазе и имеют одинаковые амплитудные значения.

Чтобы получить уравнение фазовой траектории колебательного контура, воспользуемся уравнением (1.1.10) и (1.1.11). Учтем, что колебательный импульс , тогда:

. (1.1.16)

Исключим параметр t из уравнений (1.1.10) и (1.1.16); учитывая, что 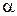=0, найдем:

, (1.1.17)

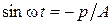. (1.1.18)

Равенства (1.1.17) и (1.1.18) возведем в квадрат и почленно сложим:

.

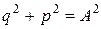Таким образом, фазовая траектория осциллятора представляет собой окружность.

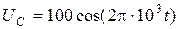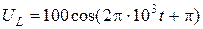ОТВЕТ: , В; , В; ; ; 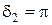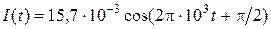, A; уравнение фазовой траектории .

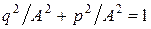ЗАДАЧА 3. Материальная точка участвует одновременно в двух колебательных процессах, происходящих в одном направлении по гармоническому закону с одинаковой частотой и амплитудами А₁= 5см, А₂= 10см и с разностью фаз 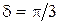. Определить амплитуду А и начальную фазу 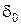результирующего колебательного процесса.

АНАЛИЗ. В задаче требуется сложить два гармонических колебаний, происходящих в одном направлении, и имеющих разные амплитуды и разность фаз.

РЕШЕНИЕ. Обозначим смещение от общего положения равновесия для каждого из процессов согласно (1.1.1) соответственно:

Для простоты, начало отсчета в момент времени t₀= 0 выберем так, чтобы 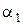= 0, тогда 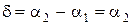. Закон движения точки, участвующий в двух колебательных процессах, определится согласно принципу суперпозиции и уравнениям движения (1.1.19) и (1.1.20):

Поскольку оба колебания – гармонические, имеющие одинаковую частоту wи одинаковое направление, результирующее колебание S (t)тоже является гармоническим и происходит с той же частотой w. Следовательно, закон движения (1.1.21) можно записать в виде

где А – амплитуда результирующего колебания, a – его начальная фаза. Сравнивая уравнения (1.1.21) и (1.1.22), получим:

Уравнение (1.1.23) справедливо для любого момента времени и поэтому является тождеством. Задача состоит в определении неизвестных А и a. Ее можно решить различными методами:

а) аналитическим методом, непосредственно решая это тождество;

б) методом векторного сложения колебаний.

Рассмотрим оба метода. В аналитическом методе используются формулы зависимости между тригонометрическими функциями двух углов. Воспользуемся зависимостью между тригонометрическими функциями двух углов:
cos(a + b)=cosacosb – sinasinb, тогда правую и левую части (1.1.23), можно представить в виде:

Полученное уравнение будет тождеством относительно переменной t, если коэффициенты при и sin 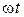в левой его части соответственно равны коэффициентам в правой части:

Чтобы найти амплитуду результирующего колебания, возведем (1.1.24) и (1.1.25) почленно в квадрат, а затем сложим:

Следовательно, м. (1.1.26)

Чтобы найти начальную фазу результирующего колебания, разделим (1.1.24) на (1.1.25):

41° = 0,23p. (1.1.27)

При расчете методом векторного сложения колебаний, последние представляются в виде векторов амплитуд 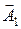и 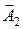, которые вращаются с угловой скоростью w против часовой стрелки (см. рис. 1.1.4). Вектор 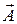амплитуды результирующего колебания равен векторной сумме векторов . Векторное сложение позволяет учесть различие в фазах колебаний (1.1.19) и (1.1.20). Из рис. 1.1.4 следует, что в данной задаче модуль вектора А проще найти, используя теорему косинусов: 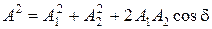, т. е. 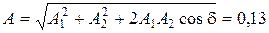м, что согласуется с результатом (1.1.26).

Угол a наклона вектора 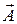к оси ОХ, как следует из диаграммы на рис. 1.1.4, равен 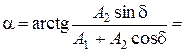41°, что также согласуется с полученным выше результатом (1.1.27).

Таким образом, результирующий колебательный процесс происходит с частотой wи описывается законом (1.1.22), где А и a определяются из равенств (1.1.26), (1.1.27) – соответственно, т. е. S(t)= 0,13cos(w t + 0,23p) , м.

ОТВЕТ: м; .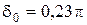

ЗАДАЧА 4. Точка одновременно участвует в n гармонических колебаниях одинаковой частоты w, направленных по одной прямой:

; ; ;.

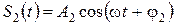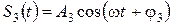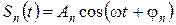. Определить амплитуду и начальную фазу результирующего колебания.

АНАЛИЗ. В задаче требуется сложить n гармонических колебаний, имеющих одинаковую частоту w. При решении необходимо использовать метод векторного сложения колебаний.

РЕШЕНИЕ. Закон движения точки, участвующей в п колебаниях, имеет вид:

Начертим соответствующую векторную диаграмму, для определенности считая, что п = 4.

Из рис. 1.1.6. видно, что проекция A_x результирующего вектора 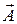на ось ОХ равна алгебраической сумме проекций векторов 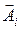отдельных колебаний:

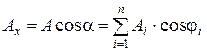. (1.1.29)

Проекция А_у результирующего колебания вектора на ось OY определяется как

. (1.1.30)

Амплитуда результирующего колебания А равна:

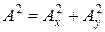. (1.1.31)

Подставим (1.1.29) и (1.1.30) в окончательную формулу (1.1.31), учитывая при этом, что 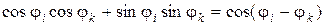, а .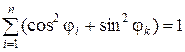

В результате получим .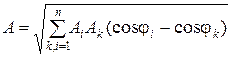

Начальная фаза результирующего колебания определится из рис. 1.1.6: .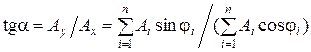

ОТВЕТ: 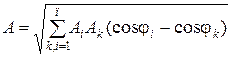; . ЗАДАЧА 5. При сложении двух гармонических колебаний одного направления результирующее колебание имеет вид: x = Acos2,1tcos50,0t, м, где t измеряется в секундах. Найти частоты складываемых колебаний и период биений.

АНАЛИЗ. В задаче требуется сложить два гармонических колебания одного направления, имеющих разную круговую частоту w.

РЕШЕНИЕ. Амплитуда рассматриваемого колебания x = Acos2,1t×cos50,0t изменяется со временем по закону:

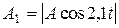. (1.1.32)

При сложении колебаний, происходящих по одному направлению с различными частотами w₁ и w₂, возникает колебательное движение, называемое биением ( ). Частота пульсаций амплитуды называется частотой биений. Амплитуда – величина существенно положительная. Следовательно, период биений равен промежутку времени, за который аргумент косинуса изменяется на p, т. е. согласно (1.1.32):

2,1Т_Б = p, с. (1.1.33)

При сложении колебаний разной частоты x₁= A₀cosw₁t и x₂= A₀cosw₂t, если их амплитуды равны, а ,уравнение результирующего колебания опишется равенством (1.1.5):

,

а его амплитуда согласно (1.1.4) имеет вид: .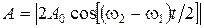

Сравним эти выражения с уравнением биений x = Acos2,1t×cos50,0t. Получим А = 2А₀,т. е. ,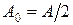

, (1.1.34)

. (1.1.35)

Из системы уравнений (1.1.34) и (1.1.35) найдем значения частот

Следовательно, биение x = A₀cos2,1tcos50,0t с периодом Т_Б= 1,5 свозникло в результате сложения колебаний с амплитудами , и частотами w₁= 47,9 рад/с, w₂= 52,1 рад/с. Их уравнения с числовыми коэффициентами имеют вид:

; .

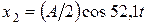ЗАДАЧА 6. На вертикально отклоняющие пластины конденсатора подается напряжение , на горизонтально отклоняющие – напряжение 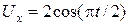. Определить траекторию луча на экране осциллографа.

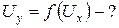
АНАЛИЗ. В задаче необходимо произвести сложение двух гармонических колебаний, происходящих во взаимно перпендикулярных плоскостях X и Y. Суммарное колебание будет одной из кривых Лиссажу, изображаемых на экране осциллографа.

РЕШЕНИЕ. Уравнение колебаний для величины напряжения U на пластинах конденсатора в общем виде можно записать, учитывая (1.1.1):

В данной задаче А₁= 2В, 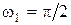рад/с, А₂= 1В, 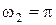рад/с, ,

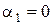т. е. . Уравнения колебаний с числовыми коэффициентами имеют вид:

(1.1.36)

. (1.1.37)

Амплитуда – величина существенно положительная и наличие знака «минус» в уравнении (1.1.37) определяется начальной фазой a₂этого колебания. Воспользовавшись формулой приведения – cospt = cos(pt + p), получим
a₂ = p. Напряжение на вертикальных пластинах опережает по фазе на pнапряжение на горизонтальных пластинах.

Чтобы определить траекторию луча на экране осциллографа, необходимо из уравнений (1.1.36) и (1.1.37) исключить параметр t (время). Поскольку по условию задачи , воспользуемся формулой для косинуса половинного угла 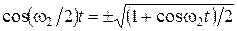. Полученное значение подставим в уравнение (1.1.36), найдем 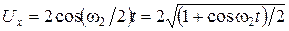, отсюда , .

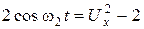Подставим полученное выражение в уравнение (1.1.37):

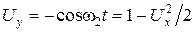, (1.1.38)

или 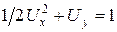. (1.1.39)

Уравнение (1.1.39) – это уравнение параболы, ось которой лежит на оси ОY. Амплитуда колебаний по оси OХ U_х = 2 В, по оси ОY – 1 В. Следовательно, абсциссы всех точек траектории заключены в пределах , а ординаты .

Для графического построения траектории воспользуемся уравнением (1.1.38) и найдем соответствующие координаты точек.

Парабола на рис. 1.1.7. построена по найденным в табл. 1.1 координатам.

lektsii.com