Журнал «Квант»
Адиабатный процесс
Адиабатный процесс — это процесс, происходящий без теплообмена системы с окружающей средой, т.е. Q = 0. Первый закон термодинамики имеет вид:
\Delta U + A = 0 \Rightarrow A = -\Delta U .\)
Это значит, что при адиабатном процессе система может выполнять работу над внешними телами только за счет убыли своей внутренней энергии. Если А > 0, то ΔU = —A 0.
Таким образом, при адиабатном расширении газ совершает работу и сам охлаждается. Наоборот, при адиабатном сжатии А \(
где γ > 1 — показатель адиабаты (или коэффициент Пуассона). Это уравнение называется уравнением адиабаты или уравнением Пуассона.
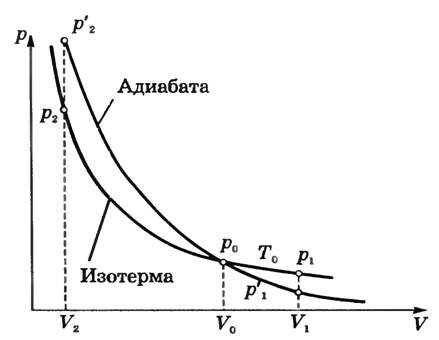
Адиабатное изменение состояния газа можно выразить графически. График этого процесса называют адиабатой. При одних и тех же начальных условиях (p0, V0) при адиабатном расширении давление газа уменьшается быстрее, чем при изотермическом (рис. 1), так как падение давления вызвано не только увеличением объема (как при изотермическом расширении), но и понижением температуры. Поэтому адиабата идет ниже изотермы и газ при адиабатном расширении совершает меньшую работу, чем при изотермическом расширении.
При быстром сжатии (расширении) теплообмен произойти не успевает и процессы можно рассматривать как адиабатные (неравновесные). Поэтому любой газ при быстром сжатии нагревается (например, нагревание насоса при накачивании велосипедной шины). При сильном и быстром сжатии воздуха температура может повыситься настолько, что при наличии в воздухе паров бензина они воспламеняются. Это используется в дизельных двигателях для зажигания горючей смеси. Этим объясняется необходимость специального охлаждения мощных компрессоров.
Охлаждение воздуха при адиабатном расширении вызывает образование облаков.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 158-159.
www.physbook.ru
Адиабатический процесс законы пуассона
АДИАБАТИЧЕСКИЙ ПРОЦЕСС — какой-либо процесс в макроскопической системе, при к-ром система не получает теплоты извне и не отдаёт её. Процесс можно считать адиабатическим, если по к.-л. причинам оказывается несущественным теплообмен между системой и окружающей средой, т. е. можно пренебречь теплопроводностью, лучистым теплообменом, поглощением и испусканием быстрых частиц. Если масса системы, участвующей в А. п., сохраняется, то изменение её внутр. энергии происходит только за счёт работы внеш. сил (первый закон термодинамики). Поэтому, напр., адиабатич. сжатие (расширение) газа сопровождается повышением (понижением) его темп-ры.
В условиях, когда не только отсутствует теплообмен с окружающей средой, но и в самой системе нет необратимого рассеяния энергии (процессы протекают равновесно), А. п. имеет характер изо-энтропического процесса (сохраняется энтропия системы).
Для классич. идеального газа связь между давлением р и темп-рой Т в изоэнтропическом процессе выражается ф-лой
где g — показатель, равный отношению Ср/Сv— теплоёмкостей газа при пост. давлении и пост. объёме.
Кривую на диаграммах состояния, характеризующую изменение параметров системы в таком А. п., наз. адиабатой, а показатель g — показателем адиабаты. Ф-лу (1) для идеального газа можно записать также в виде T V g-1 = const и pV g = const (ур-ние Пуассона). Для нерелятивистского невырожденного одноатомного идеального газа Ср = 5nRoТ/2, Сv= 3nRoT/2 (где n — число молей, Ro — универсальная газовая постоянная ) и g = 5 /3, а для двухатомного газа g = 7 /5. В случае, когда давление определяется ультрарелятивистским газом электронов, энергия к-рых много больше их массы покоя , ур-ние А. п. совпадает с ур-нием Пуассона при g = 4 /3, но здесь g уже не явл. отношением теплоёмкостей. В астрофизике примером А. п. может служить адиабатич. стадия расширения остатков вспышек сверхновых звёзд. На протяжении этой стадии энергия газа внутри остатка (за фронтом сферической ударной волны, распространяющейся по межзвёздному газу) существенно превышает его суммарные потери энергии на излучение. Типичные остатки сверхновых могут находиться на адиабатич. стадии в течение неск. десятков тыс. лет.
В теории пульсаций звёзд рассматриваются адиабатич. колебания вещества звезды, позволяющие установить зависимость осн. периода радиальных колебаний звезды Р от её ср. плотности r и строения:
где W — параметр, равный 1 для однородной звезды и больше 1 для др. моделей строения звёзд.
В распространении адиабатич. возмущений (типа звуковых волн) в космич. веществе на ранних стадиях расширения Вселенной совр. космология видит одну из возможных причин появления неоднородностей во Вселенной — зачатков её будущей структуры (галактик и скоплений галактик, см. Космология ).
Лит.:
Зельдович Я. Б., Новиков И. Д., Строение и эволюция Вселенной, М., 1975
Новиков И. Д., Эволюция Вселенной, М., 1979.
www.astronet.ru
Адиабатический процесс и политропный процесс
Адиабатическим называется процесс, при котором отсутствует теплообмен ( d Q =0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.
Из первого начала термодинамики ( d Q = dU + d A ) для адиабатического процесса следует, что
 (55.1)
(55.1)
т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
Используя выражения (52.1) и (53.4), для произвольной массы газа перепишем уравнение (55.1) в виде
 (55.2)
(55.2)
Продифференцировав уравнение состояния для идеального газа  получим
получим
 (55.3)
(55.3)
Исключим из (55.2) и (55.3) температуру Т.

Разделив переменные и учитывая, что С p /С V = g (см. (53.8)), найдем

Интегрируя это уравнение в пределах от p 1 до p 2 и соответственно от V 1 до V 2, а затем потенцируя, придем к выражению

Так как состояния 1 и 2 выбраны произвольно, то можно записать
 (55.4)
(55.4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Для перехода к переменным Т, V или p , Т исключим из (55.4) с помощью уравнения Клапейрона — Менделеева

соответственно давление или объем:
 (55.5)
(55.5)
 (55.6)
(55.6)
Выражения (55.4) — (55.6) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина (см. (53.8) и (53.2))
 (55.7)
(55.7)
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов ( Ne , He и др.), достаточно хорошо удовлетворяющих условию идеальности, i =3, g =1,67. Для двухатомных газов (Н2, N 2, О2 и др.) i =5, g =1,4. Значения g , вычисленные по формуле (55.7), хорошо подтверждаются экспериментом.
Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис. 83). На рисунке видно, что адиабата ( pV g = const ) более крута, чем изотерма ( pV = const ). Это объясняется тем, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение (55.1) в виде

Если газ адиабатически расширяется от объема V 1 до V 2, то его температура уменьшается от T 1 до T 2 и работа расширения идеального газа
 (55.8)
(55.8)
Применяя те же приемы, что и при выводе формулы (55.5), выражение (55.8) для работы при адиабатическом расширении можно преобразовать к виду

где  .
.
Работа, совершаемая газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 83), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С V и С p , в изотермическом процессе ( dT =0) теплоемкость равна ± ¥ , в адиабатическом ( d Q =0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости ( C = const ) можно вывести уравнение политропы:
 (55.9)
(55.9)
где п=(С—С p )/(С—С V )—показатель политропы. Очевидно, что при С=0, n = g , из (55.9) получается уравнение адиабаты; при С = ¥ , n = 1 — уравнение изотермы; при С=С p , n =0 —уравнение изобары, при С=С V , n =± ¥ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
www.pppa.ru
Адиабатный процесс (закон Пуассона, 1823 г.)
(французский физик и математик Симеон Дени Пуассон,1781-1840).
Процесс, происходящий без теплообмена с окружающей средой, называется адиабатным, т. е. q = 0. Для того чтобы осуществить такой процесс, следует либо теплоизолировать газ, т. е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Как правило, это возможно, ибо теплообмен происходит значительно медленнее, чем сжатие или расширение газа.
Параметры адиабатного процесса находятся путём решения дифференциального уравнения первого закона термодинамики, которое для адиабатного процесса принимает вид:
Преобразовав и проинтегрировав, получаем
Это и есть уравнения адиабаты идеального газа при постоянном отношении теплоемкостей (k = const).
называется показателем адиабаты. Согласно классической кинетической теории теплоемкость газов не зависит от температуры, поэтому можно считать, что величина k также не зависит от температуры и определяется числом степеней свободы молекулы. Для одноатомного газа k = 1,66, для двухатомного k = 1,4, для трех- и многоатомных газов k =1,33.

Поскольку k > 1, то в координатах р- v (рис. 4.4) линия адиабаты идет круче линии
изотермы, таким образом при адиабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.
В адиабатном процессе Δq = сад = 0.
studopedia.ru

Адиабатный процесс
Адиабатным процессом называют процесс изменения термодинамического состояния, происходящий без теплообмена с окружающей средой.
Какой процесс можно было бы считать адиабатным? Вопрос не столь простой. Условием адиабатности можно считать следующее условие: с одной стороны — процесс должен быть очень быстрым, чтобы за время процесса не успел произойти теплообмен, а с другой стороны — он должен быть медленным, чтобы промежуточные состояния были обратимыми (квазистатичными) .
Процесс без теплообмена не является адиабатным, если он протекает настолько быстро, что промежуточные состояния не являются квазистатическими (обратимыми).
Если в цилиндре поршень сжимает газ, то в каждый момент времени давление и температура газа должны быть одинаковыми по всему объёму. Для осуществления этого требования требуется некоторое время, называемое временем релаксации. Иначе поршень будет «сгребать» перед собой «сугроб» из молекул.
Первый закон термодинамики для адиабатного процесса будет иметь вид:
Если работа, совершаемая над газом внешними телами, будет положительной (отрицательной), то изменение внутренней энергии тоже будет положительным (отрицательным), следовательно, газ нагревается (остывает).
Пусть из некоторого одинакового начального состояния начинают расширяться две одинаковые порции газа. Одна порция расширяется изотермически, другая адиабатно. При увеличении объёмов газов на некоторую величину изотермический процесс приведёт к снижению давления только потому, что уменьшится концентрация молекул. В адиабатном же расширении газ уменьшает внутреннюю энергию и остывает. Давление при этом уменьшится за счёт уменьшения концентрации так же, как в и изотермическом процессе, но при этом давление ещё дополнительно уменьшится из-за уменьшения температуры. Поэтому давление в адиабатном процессе падает быстрее, чем в изотермическом процессе. Данный факт означает, что график адиабатного процесса в координатной плоскости рV будет пересекать график изотермического процесса. На качественном уровне мы уже приходим к выводу, что график адиабаты круче изотермы (рис. 13).
Уравнение, отображающее изменения термодинамических параметров при адиабатном квазистатическом процессе, называют уравнением Пуассона. Не задаваясь целью рассмотрения вывода уравнения, запишем его в готовом виде в различных формах.
zftsh.online
